Lista de Exercícios 5
Contents
Lista de Exercícios 5#
Solucionário matemático e computacional de exercícios selecionados da Lista de Exercícios 5.
%matplotlib inline
# importação de módulos
import numpy as np
import matplotlib.pyplot as plt
Ajuste de curvas#
Obs.:: função polyfit retorna coeficientes da curva de ajuste na ordem:
P = p[0] + p[1]*x + p[2]*x**2 + p[3]*x**3 + ...
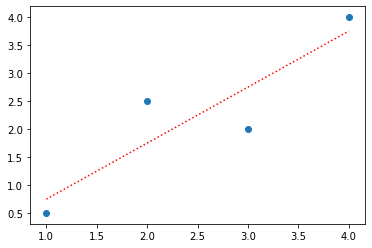
Exemplo: solução fechada 2D#
# tabela de dados
x = np.array([1,2,3,4])
y = np.array([0.5,2.5,2.0,4.0])
# min quad
m = np.size(x)
alpha1 = (m*np.dot(x,y) - np.sum(x)*np.sum(y))/(m*np.dot(x,x)-np.sum(x)**2)
alpha0 = np.mean(y) - alpha1*np.mean(x)
# plot
plt.scatter(x,y)
y2 = alpha0 + alpha1*x
plt.plot(x,y2,'r:');
Resolução da Lista 5#
Função-base para computar ajuste e plotar resultados#
"""
Resolve problema de ajuste polinomial discreto e plota resultado
entrada:
x,y : tabela de valores (numpy arrays)
g : grau do polinômio de ajuste (int)
"""
def resolve_ajuste(x,y,g):
c = np.polyfit(x, y, g) # ajuste
p = np.poly1d(c)
plt.plot(x,y,'d',x,p(x),'o-')
plt.xlabel(str(x))
for i in range(g+1):
print('Coeficiente de ajuste p[' + str(i) + ']: ' + str(c[i]))
return p
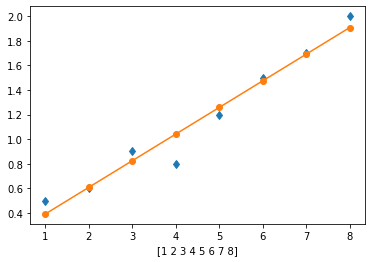
L5-Q2#
Ajuste os dados abaixo pelo método dos mínimos quadrados:
\begin{array}{c|cccccccc} x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ \hline y & 0.5 & 0.6 & 0.9 & 0.8 & 1.2 & 1.5 & 1.7 & 2.0 \end{array}
a) por reta
b) por parábola do tipo \(ax^2 + bx + c\);
Solução#
Metodologia matemática#
a)
\begin{array}{c|cccccccc} g_1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ \hline g_2 & 1 & 1 & 1& 1& 1 & 1 & 1 & 1 \ \hline f & 0.5 & 0.6 & 0.9 & 0.8 & 1.2 & 1.5 & 1.7 & 2.0 \end{array}
b)
\(g_1(x) = x^2\); \(g_2(x)=x\); \(g_3(x)=1\)
\begin{array}{c|cccccccc} g_1 & 1 & 4 & 9 & 16 & 25 & 36 & 49 & 64 \ \hline g_2 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ \hline g_3 & 1 & 1 & 1& 1& 1 & 1 & 1 & 1 \ \hline f & 0.5 & 0.6 & 0.9 & 0.8 & 1.2 & 1.5 & 1.7 & 2.0 \end{array}
Metodologia computacional#
a)
# tabela de dados
x = np.arange(1,9)
y = np.array([0.5,.6,.9,.8,1.2,1.5,1.7,2.])
# grau 1
g = 1
p = resolve_ajuste(x,y,g)
Coeficiente de ajuste p[0]: 0.2166666666666667
Coeficiente de ajuste p[1]: 0.17499999999999996
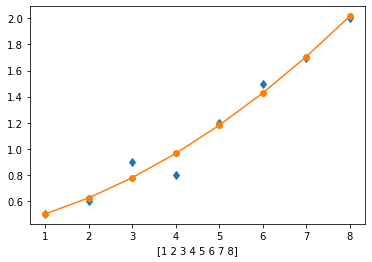
b)
# grau 2
g = 2
p = resolve_ajuste(x,y,g)
Coeficiente de ajuste p[0]: 0.015476190476190437
Coeficiente de ajuste p[1]: 0.07738095238095268
Coeficiente de ajuste p[2]: 0.407142857142857
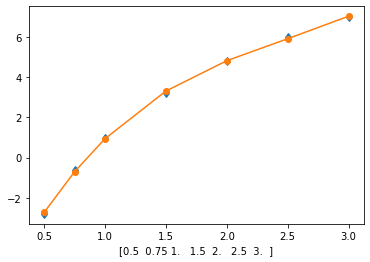
L5-Q3#
Dada a tabela abaixo, faça o gráfico de dispersão dos dados e ajuste uma curva da melhor maneira possı́vel:
\begin{array}{c|cccccc} x & 0.5 & 0.75 & 1 & 1.5 & 2.0 & 2.5 & 3.0 \ \hline y & -2.8 & -0.6 & 1& 3.2& 4.8 & 6.0 & 7.0 \end{array}
Solução#
Metodologia matemática#
\(g_1(x) = 1\); \(g_2(x)=x\); \(g_3(x)=x^2\); \(g_4(x)=x^3\)
\begin{array}{c|cccccc} g_1 & 1 & 1 & 1& 1& 1 & 1 & 1 \ g_2 & 0.5 & 0.75 & 1 & 1.5 & 2.0 & 2.5 & 3.0 \ \hline g_3 & 0.25 & 0.5625& 1& 2.25& 4 & 6.25 & 9.0\ \hline g_4 & 0.1250 & 0.4219 & 1& 3.375& 8 &15. 625 & 27 \ f & -2.8 & -0.6 & 1& 3.2& 4.8 & 6.0 & 7.0 \end{array}
Metodologia computacional#
# tabela
x = np.array([0.5,0.75,1,1.5,2.0,2.5,3.0])
y = np.array([-2.8,-0.6,1,3.2,4.8,6.0,7.0])
# grau (teste para g = 2,3,4,5 e veja o erro)
g = 3
p = resolve_ajuste(x,y,g)
# erro
np.sum((p(x)-y)**2)
Coeficiente de ajuste p[0]: 0.588808229974697
Coeficiente de ajuste p[1]: -4.365386461549416
Coeficiente de ajuste p[2]: 12.85159200943416
Coeficiente de ajuste p[3]: -8.131256481519904
0.040251260748212274
L5-Q4#
A tabela abaixo mostra as alturas e pesos de nove homens entre as idades de 25 a 29 anos extraı́da ao acaso entre funcionários de uma grande indústria:
\begin{array}{c|ccccccccc} \text{Altura/cm} & 183& 173 & 168 & 188 & 158 & 163 & 193 &163 &178 \ \hline \text{Peso/kg} & 79 & 69 & 70& 81 & 61 &63 &79 & 71 & 73 \end{array}
Metodologia matemática#
\(g_1(x) = 1\); \(g_2(x)=x\)
\begin{array}{c|cccccccc} g_1 & 1 & 1 & 1& 1& 1 & 1 & 1 & 1&1\ \hline g_2 & 183& 173 & 168 & 188 & 158 & 163 & 193 &163 &178 \ \hline f & 79 & 69 & 70& 81 & 61 &63 &79 & 71 & 73 \end{array}
Metodologia computacional#
altura = np.array([183,173,168,188,158,163,193,163,178])
peso = np.array([79,69,70,81,61,63,79,71,73])
# gráfico de dispersão
plt.scatter(altura,peso)
<matplotlib.collections.PathCollection at 0x7fc4720ed610>
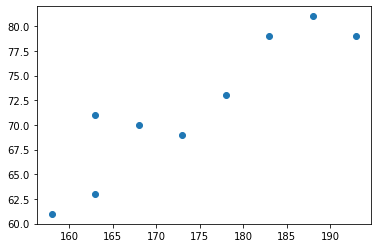
solucao-L5-Q4-b#
# ajuste da reta
p = resolve_ajuste(altura,peso,1)
Coeficiente de ajuste p[0]: 0.527570093457944
Coeficiente de ajuste p[1]: -20.078037383177612
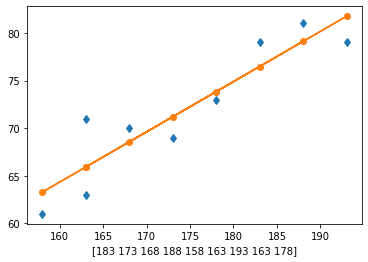
solucao-L5-Q4-c#
# estimativa de peso (kg)
alt = 175
p_c = p(alt)
print(p_c)
# estimativa de altura (cm)
alt = 80
a_c = (alt - p[0])/p[1]
print(a_c)
72.2467289719626
189.69619131975205
solucao-L5-Q4-d#
p2 = resolve_ajuste(peso,altura,1)
Coeficiente de ajuste p[0]: 1.5856741573033717
Coeficiente de ajuste p[1]: 60.294943820224695
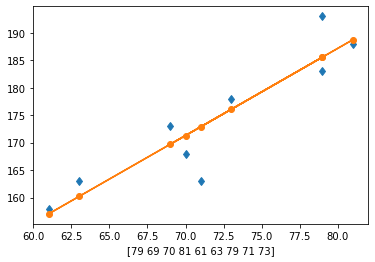
solucao-L5-Q4-e#
# estimativa de peso a partir de altura com novo ajuste
alt = 175
p_e = (alt - p2[0])/p2[1]
print(p_e)
# comparação com item (c): pesos
# pequena diferença entre os valores
dif = abs(p_c-p_e)
print(dif)
72.33835252435782
0.09162355239521958
solucao-L5-Q4-f#
# comparação das retas de ajuste
# influência do resíduo => inclinações diferentes
plt.plot(altura,p(altura),altura,(altura - p2[0])/p2[1])
[<matplotlib.lines.Line2D at 0x7fc4724d15d0>,
<matplotlib.lines.Line2D at 0x7fc4724d1810>]
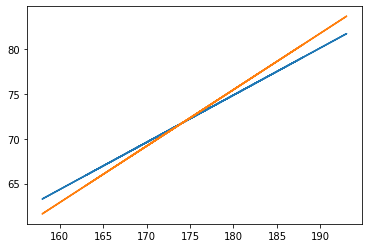
solucao-L5-Q5-a#
AJUSTE POR RETA#
"""
Nota: pesquisa no IBGE em maio de 2018
mostra que a população já rompeu 209 mi.
"""
# tabela de dados
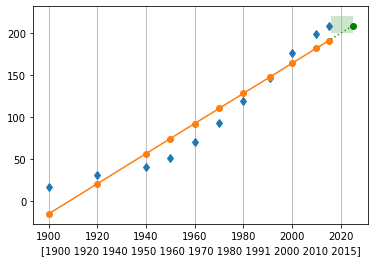
ano = np.array([1900, 1920, 1940, 1950, 1960, 1970, 1980, 1991, 2000, 2010, 2015])
hab = np.array([17.4, 30.6, 41.2, 51.9, 70.2, 93.1, 119.0, 146.2, 175.8, 198.6, 207.8])
# plotagem
fig,ax = plt.subplots(1,1)
p = resolve_ajuste(ano,hab,1)
ax.grid(axis='x')
# plotagem do comportamento preditivo
# linha tracejada e area
ano_m = np.linspace(2016, 2025, num=10, endpoint=True)
v2 = np.ones(np.shape(ano_m))
ax.fill_between(ano_m,200*v2,220*v2,facecolor='g',alpha=0.2)
plt.plot(ano_m,p(ano_m),':')
plt.plot(2025,p(2025),'go')
# estimativa no ano 2025
p(2025)
Coeficiente de ajuste p[0]: 1.7924185769967504
Coeficiente de ajuste p[1]: -3420.8153029001523
208.83231551826748
# abrindo vetor de 1900 a 2024
anos = np.arange(ano[0],ano[-1]+10)
pops = p(anos) # população
# encontrando ano em que a populacao superou 100 mi
lim100 = np.nonzero(pops>100)
lim150 = np.nonzero(pops>150)
lim200 = np.nonzero(pops>200)
np.shape(lim100)
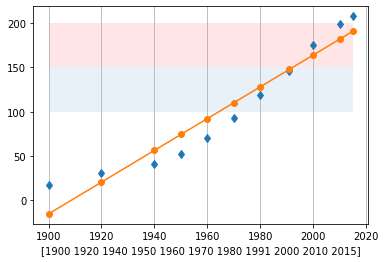
print('Marca de 100 milhões de pessoas: ' + str(anos[lim100[0][0]]))
print('Marca de 150 milhões de pessoas: ' + str(anos[lim150[0][0]]))
print('Marca de 200 milhões de pessoas: ' + str(anos[lim200[0][0]]))
Marca de 100 milhões de pessoas: 1965
Marca de 150 milhões de pessoas: 1993
Marca de 200 milhões de pessoas: 2021
# plotagem por faixas de valores
fig,ax = plt.subplots(1,1)
p = resolve_ajuste(ano,hab,1)
ax.grid(axis='x')
v1 = np.ones(np.shape(ano))
ax.fill_between(ano,100*v1,150*v1,alpha=0.1)
ax.fill_between(ano,150*v1,200*v1,facecolor='r',alpha=0.1)
Coeficiente de ajuste p[0]: 1.7924185769967504
Coeficiente de ajuste p[1]: -3420.8153029001523
<matplotlib.collections.PolyCollection at 0x7fc47246b410>
AJUSTE POR PARÁBOLA#
# plotagem
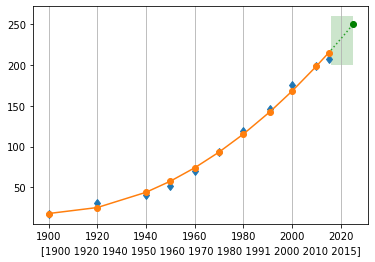
fig,ax = plt.subplots(1,1)
p = resolve_ajuste(ano,hab,2)
ax.grid(axis='x')
# plotagem do comportamento preditivo
# linha tracejada e area
ano_m = np.linspace(2016, 2025, num=10, endpoint=True)
v2 = np.ones(np.shape(ano_m))
ax.fill_between(ano_m,200*v2,260*v2,facecolor='g',alpha=0.2)
plt.plot(ano_m,p(ano_m),':')
plt.plot(2025,p(2025),'go')
# estimativa no ano 2025
p(2025)
Coeficiente de ajuste p[0]: 0.01418349430843006
Coeficiente de ajuste p[1]: -53.81354030390032
Coeficiente de ajuste p[2]: 51061.1779002923
249.95013340016885
# abrindo vetor de 1900 a 2024
anos = np.arange(ano[0],ano[-1]+10)
pops = p(anos) # população
# encontrando ano em que a populacao superou 100 mi
lim100 = np.nonzero(pops>100)
lim150 = np.nonzero(pops>150)
lim200 = np.nonzero(pops>200)
np.shape(lim100)
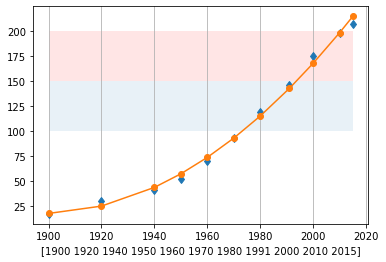
print('Marca de 100 milhões de pessoas: ' + str(anos[lim100[0][0]]))
print('Marca de 150 milhões de pessoas: ' + str(anos[lim150[0][0]]))
print('Marca de 200 milhões de pessoas: ' + str(anos[lim200[0][0]]))
Marca de 100 milhões de pessoas: 1974
Marca de 150 milhões de pessoas: 1994
Marca de 200 milhões de pessoas: 2011
# plotagem por faixas de valores
fig,ax = plt.subplots(1,1)
p = resolve_ajuste(ano,hab,2)
ax.grid(axis='x')
v1 = np.ones(np.shape(ano))
ax.fill_between(ano,100*v1,150*v1,alpha=0.1)
ax.fill_between(ano,150*v1,200*v1,facecolor='r',alpha=0.1)
Coeficiente de ajuste p[0]: 0.01418349430843006
Coeficiente de ajuste p[1]: -53.81354030390032
Coeficiente de ajuste p[2]: 51061.1779002923
<matplotlib.collections.PolyCollection at 0x7fc471ff9310>
Integração Numérica#
Função-base para integrais de Newton-Cotes#
def integral_newton_cotes(x,y,metodo):
# diff computa h = x[k+1] - x[k];
# duplo diff retorna 0 se igualmente espaçado
h = np.diff(x)
hh = np.diff(h)
# verifica se vetor é, de fato, de zeros, dentro de tolerância
# se não, lança erro
np.testing.assert_allclose(hh, 0*hh, atol=1e-08)
# switch
if metodo is 'trapezio':
# montando vetor de somas y[k] + y[k+1]
cs = np.cumsum(y)
u = np.concatenate((np.array([0]),cs[0:-2]))
ss = cs[1:]-u # somas
# integral (regra generalizada)
integral = h[0]/2*np.sum(ss)
elif metodo is 'simpson13':
if np.size(x) % 2 is 0:
raise ValueError('Regra de Simpson válida apenas para número ímpar de pontos.')
# constroi pesos
# ignora primeiro e ultimo
ie = np.array(range(0,np.size(x)))
ie = ie[1:-1] % 2
# pesos para intermediarios
for v in range(np.size(ie)):
if ie[v] == 1:
ie[v] = 4
elif ie[v] == 0:
ie[v] = 1
# concatena para recriar
ie = np.concatenate(([1],ie,[1]))
# integral (regra generalizada)
integral = h[0]/3*(np.sum(y*ie))
return integral
Exemplo#
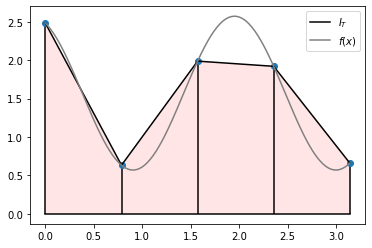
Integração numérica pela regra do trapézio para a função $\(\int_{a=0}^{b=\pi} [ {\rm sen}(3x + 2) + 0.5\pi ] \, dx \approx I_T \)$
# função
a = 0
b = np.pi
x = np.linspace(a,b,num=5,endpoint=True)
f = lambda x: np.sin(3*x + 2) + np.pi/2
y = f(x)
# integração por trapézio
integral_newton_cotes(x,y,'trapezio')
4.799420241706493
# plotagem dos trapézios
plt.stem(x,y,'-ok',basefmt='k-',use_line_collection=True)
plt.plot(x,y,'-k',label='$I_T$')
plt.fill_between(x,0*y,y,facecolor='r',alpha=0.1)
# "imitação" da função contínua
xx = np.linspace(a,b,num=200,endpoint=True)
plt.plot(xx,f(xx),color=[0.5,0.5,0.5],label='$f(x)$')
plt.legend();
Exemplo#
Idem, para regra 1/3 de Simpson \(I_S\)
# integração por 1/3 Simpson
integral_newton_cotes(x,y,'simpson13')
4.016218444253924
Função residente em Python para integração#
import scipy.integrate as sp
Exemplo#
Mesma função \(f(x)\), agora calculada com o Scipy.
# scipy::quad (erro absoluto)
integral_ = sp.quad(f,a,b)
integral_
(4.657370976179917, 1.5031433917569477e-13)
solucao-L5-Q9#
# dados
x = np.array([1.00, 1.05, 1.10, 1.15, 1.20, 1.25, 1.30])
y = np.array([1.0000, 1.0247, 1.0488, 1.0723, 1.0954, 1.1180, 1.1401])
# integral implementada: trapézio
print(integral_newton_cotes(x,y,'trapezio'))
# integral implementada: 1/3 Simpson
print(integral_newton_cotes(x,y,'simpson13'))
# integral scipy: 1/3 Simpson
f = lambda x: np.sqrt(x)
sp.quad(f,x[0],x[-1])
0.32146250000000026
0.2857383333333336
(0.32148536841925296, 3.569204580991558e-15)
solucao-L5-Q10#
# caso h = 0.1
x = np.array([0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])
y = np.array([1, 0.995, 0.980, 0.955, 0.921, 0.877, 0.825, 0.764, 0.696, 0.6216, 0.5403])
print(integral_newton_cotes(x,y,'trapezio'))
# integral implementada: 1/3 Simpson
print(integral_newton_cotes(x,y,'simpson13'))
# residente
f = lambda x: np.cos(x)
print(sp.quad(f,x[0],x[-1]))
# caso h = 0.2
x2 = np.concatenate((x[0:-1:2],[1]))
y2 = np.concatenate((y[0:-1:2],[0.5403]))
print(integral_newton_cotes(x2,y2,'trapezio')) # TODO <=== CHECAR ISTO AQUI!
# integral implementada: 1/3 Simpson
print(integral_newton_cotes(x2[0:-1],y2[0:-1],'simpson13'))
# residente
print(sp.quad(f,x2[0],x2[-1]))
0.8404750000000001
0.7270900000000001
(0.8414709848078965, 9.34220461887732e-15)
0.83843
0.6557999999999999
(0.8414709848078965, 9.34220461887732e-15)
solucao-L5-Q11#
x = np.array([1.2, 1.3, 1.4, 1.5, 1.6])
y = np.array([0.93204, 0.96356, 0.98545, 0.99749, 0.99957])
print(integral_newton_cotes(x,y,'trapezio'))
# integral implementada: 1/3 Simpson
print(integral_newton_cotes(x,y,'simpson13'))
# residente
f = lambda x: np.sin(x)
print(sp.quad(f,x[0],x[-1]))
0.39123050000000037
0.35870866666666695
(0.3915572767779624, 4.34715904138419e-15)
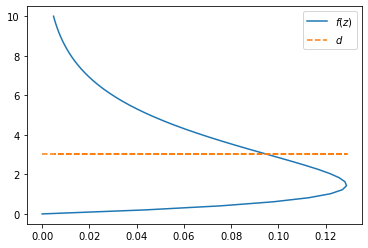
solucao L5-Q17#
z = np.linspace(0,10,num=50,endpoint=True)
f = lambda z: z/(4+z)*np.exp(-0.5*z)
d = integral_newton_cotes(z,z*f(z),'trapezio')/integral_newton_cotes(z,f(z),'trapezio')
print(d)
# residente
f2 = lambda z: ( z/(4+z)*np.exp(-0.5*z) )*z
print(sp.quad(f2,0,10)[0]/sp.quad(f,0,10)[0])
3.0523917901871935
3.0476097824918496
# plotagem da força
plt.plot(f(z),z,label='$f(z)$')
plt.plot(f(z),np.ones(np.shape(f(z)))*d,'--',label='$d$')
plt.legend();
QUADRATURA GAUSSIANA#
Algumas informações:
A quadratura gaussiana pode ser chamada como
from scipy.integrate import quadrature
Depois de importar, veja
help(quadrature)
A tabela de pesos de quadratura pode ser acessada no Numpy através do comando
np.polynomial.legendre.leggauss(ord)
Integra exatamente polinômios de grau até
2*ord - 1
solucao-L5-Q18a#
from scipy.integrate import quadrature
# integração
f = lambda z: z**3 + z**2 + z + 1
quadrature(f, -1, 1,maxiter=3) # grau máximo = 3; erro = 0
(2.6666666666666665, 0.0)
# Verificando computação numérica x simbólica com Sympy
import sympy as sy
# cria símbolo para z
zsym = sy.Symbol('z')
# integração
f = zsym**3 + zsym**2 + zsym + 1
val = sy.integrate(f, (zsym,-1,1))
float(val)
2.6666666666666665
solucao-L5-Q18b#
# integração
f = lambda x: x**2 -1
quadrature(f, -2, 0,maxiter=3)
(0.666666666666667, 2.220446049250313e-16)
# integração simbólica
f = zsym**2 + -1
val = sy.integrate(f, (zsym,-2,0))
float(val)
0.6666666666666666
Exemplos de integrandos com singularidades#
Esses casos não são bem manipulados pelo submódulo integrate.
solucao-L5-Q18c#
# função com singularidade
# integração
f = lambda x: ((1-x**2)**(-1/2))*x**2*x**2
quadrature(f, -1, 1)
/Users/gustavo/anaconda3/lib/python3.7/site-packages/scipy/integrate/quadrature.py:251: AccuracyWarning: maxiter (50) exceeded. Latest difference = 6.973792e-04
AccuracyWarning)
(1.1436022273829545, 0.0006973792417572788)
solucao-L5-Q18d#
# função com singularidade
# integração
f = lambda x: (x**3 +2*x**2)/(4*(4-x**2)**1/2)
quadrature(f, -2, 2,maxiter=3)
/Users/gustavo/anaconda3/lib/python3.7/site-packages/scipy/integrate/quadrature.py:251: AccuracyWarning: maxiter (3) exceeded. Latest difference = 1.333333e+00
AccuracyWarning)
(3.3333333333333357, 1.333333333333336)

