EDOs de ordem superior (redução de ordem)
Contents
38. EDOs de ordem superior (redução de ordem)#
EDOs de ordem superior podem ser reescritas como sistemas de EDOs de primeira ordem. A fim de verificarmos como isto pode ser feito, consideremos, inicialmente o caso geral de uma EDO de segunda ordem.
Se fizermos \(y_1(t) = y(t)\) e \(y_2(t) = y'(t)\), o PVI acima pode ser reformulado como um sistema de duas EDOs de primeira ordem como:
38.1. Movimento pendular simples#
Como exemplo (simplificado) prático derivado de uma EDO de segunda ordem, temos o movimento de um pêndulo submetido apenas à força gravitacional como mostra a figura abaixo. O pêndulo de massa \(m\) fica pendurado por uma corda de comprimento \(l\) e se move em relação ao eixo \(\theta = 0\). O movimento é completamente descrito com a especificação da posição inicial \(\theta(0) = \theta_0\) e a velocidade angular inicial \(\theta'(0) = \theta_0'\).
import numpy as np
import matplotlib.pyplot as plt
#plt.autoscale(enable=True, axis='x', tight=True)
plt.figure(figsize=(3,3))
theta = np.pi/10
x = np.linspace(0,1,10)
plt.axvline(x=0.5,ymin=0,ymax=1.0,linestyle='--',linewidth=1.0)
plt.plot([0.5,0.5 + np.sin(theta)],[1.0,1.0-np.cos(theta)],linewidth=1.0)
plt.scatter([0.5 + np.sin(theta)],[1.0-np.cos(theta)],s=300)
plt.box(False); locs, labels = plt.xticks(); plt.tick_params(axis='both',width=0.0,labelleft=False,labelbottom=False)
x1,x2 = plt.xlim([0,1])
y1,y2 = plt.ylim([-0.3,1])
plt.annotate('$\\theta$',xy=(0.52,0.72),fontsize=14);
Uma vez que o comprimento do arco realizado pelo pêndulo é \(s = l\theta\) e a força-peso tangente ao arco oposta ao movimento é determinada em função de \(\theta\) por \(-mg{\rm sen}(\theta)\), a segunda lei de Newton diz-nos que
Tomando a EDO acima juntamente com as condições iniciais e valendo-se das substituições \(y_1(t) = \theta(t)\) e \(y_2(t) = \theta'(t)\), obtemos um sistema de EDOs de primeira ordem que nos conduz ao seguinte PVI: $\(\begin{cases} y_1'(t) = y_2(t) \\ y_2'(t) = - \dfrac{g}{l}{\rm sen}(\theta) \\ y_1(0) = \theta(0) = \theta_0 \\ y_2(0) = \theta'(0) = \theta_0' \end{cases}\)$
38.2. Hipótese de ângulos pequenos#
No movimento pendular, se \(\theta\) for considerado muito pequeno, podemos dizer que \(\theta \approx {\rm sen}(\theta)\). Logo, a EDO de segunda ordem reduz-se a
de maneira que, analogamente ao caso anterior, temos um novo sistema levemente modificado na segunda equação: $\(\begin{cases} y_1'(t) = y_2(t) \\ y_2'(t) = - \dfrac{g}{l}y_1(t) \\ y_1(0) = \theta(0) = \theta_0 \\ y_2(0) = \theta'(0) = \theta_0' \end{cases}\)$
Vale dizer que a solução analítica para este caso é dada por \(\theta(t) = \theta_0 \cos \left( \sqrt{\dfrac{g}{l}} t \right)\).
38.3. Caso geral de ordem \(m\)#
De modo similar, uma EDO de ordem \(m\) pode gerar um sistema de EDOs de ordem 1. Considerando o PVI generalizado $\(\begin{cases} \dfrac{d^m y(t)}{dt^m} = f(t,y,y',\ldots,y^{(m-1)}) \\ y(t_0) = y_0, \ \ y'(t_0) = y_0', \ldots y^{(m-1)}(t_0) = y_0^{(m-1)}, \end{cases}\)$ usamos as substituições
para reformular o PVI original no sistema:
Exemplo: O PVI
pode ser reformulado no sistema
Exercício resolvido: utilizando os parâmetros \(g=9.867 \, m/s^2\), \(\theta_0 = \pi/25\) e \(\theta_0' = 0.5 \, m/s\), resolva numericamente o sistema de EDOs do movimento pendular sob a hipótese de ângulos pequenos.
Para resolver o exercício, utilizaremos o método de Euler que implementamos anteriormente. Basta definirmos uma nova função fsys e os parâmetros necessários para o funcionamento da função euler_sys.
from numpy import *
def euler_sys(t0,tf,y0,h,f):
"""
Resolve o PVI de um sistema de EDOs escalares
y’ = f(t,y), t0 <= t <= b, y(t0)=y0 pelo metodo de Euler com tamanho de passo h.
O usuario deve fornecer um vetor f contendo as funcoes a serem avaliadas como
membro direito.
Entrada:
t0 - tempo inicial
tf - tempo final
y0 - condicao inicial
h - passo
f - vetor de funcoes f(t,y) (anonima)
Saída:
t - vetor contendo os valores nodais t[i], i = 1,2,...,n
Y - matriz de dimensoes n x m, com m sendo o numero de EDOs
(a i-esima linha y[i,:] traz as estimativas de todas
as funcoes y_j no tempo t[i])
"""
m = y0.size
n = round((tf - t0)/h + 1)
t = linspace(t0,t0+(n-1)*h,n)
Y = zeros((n,m))
Y[0,:] = y0
for i in range(1,n):
Y[i,:] = Y[i-1,:] + h*f(t[i-1],Y[i-1,:])
return t,Y
# define funcao f(t,y)
def params(g,l):
return g,l
def fsys(t,y):
aux = params(g,l)
# considera g e l como parâmetros
F = array([y[1],-aux[0]/aux[1]*y[0]])
return F
from matplotlib.pyplot import plot,legend
# parametros
t0,tf = 0,5
h = 0.05
theta0 = np.pi/25
dtheta0 = 0.5
y0 = array([theta0,dtheta0])
g, l = 9.867, 1.0
# solucao numerica do sistema
t,Y = euler_sys(t0,tf,y0,h,fsys)
y1_num = Y[:,0]
y2_num = Y[:,1]
# solucao analitica
y1_an = theta0*np.cos(np.sqrt(g/l)*t)
# plotagem
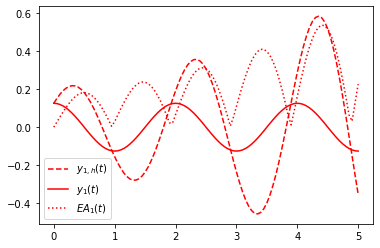
plot(t,y1_num,'r--',label='$y_{1,h}(t)$')
#plot(t,y2_num,'b--',label='$y_{2,h}(t)$')
plot(t,y1_an,'r',label='$y_1(t)$')
#plot(t,y2_an,'b',label='$y_2(t)$')
# erro absoluto
plot(t,abs(y1_an - y1_num),'r:',label='$EA_1(t)$')
#plot(t,abs(y2_an - y2_num),'b:',label='$EA_2(t)$')
legend(loc=3,fontsize=10)
<matplotlib.legend.Legend at 0x7fb2d222e100>
Exercício: Converta as EDOs de ordem superior abaixo para sistemas de EDOs escalares.
Solução analítica: \(y(t) = \exp(-t) + t^2\).
Solução analítica: \(y(t) = 3\cos(t) + {\rm sen}(t) + \exp(-2t){\rm sen}(3t)\).
38.4. Problemas#
Problema: Converta o seguinte sistema de EDOs de 2a. ordem para um sistema maior de EDOs de primeira ordem. Este sistema surge do estudo da atração gravitacional de uma massa por outra:
onde \(c\) é uma constante positiva e \(r(t) = [x(t)^2 + y(t)^2 + z(t)^2]^{1/2}\), com \(t\) denotando o tempo.
Problema: Resolva o problema do pêndulo numericamente pelo método de Euler. Considere \(l = 1\) e \(g = 32.2 \, pés/s^2\). Como valores iniciais, escolha \(0 < \theta(0) \le \pi/2\) e \(\theta'(0) = 1\). Experimente vários valores de \(h\) de modo a obter erros pequenos. Plote os gráficos \(t \, vs. \, \theta(t)\), \(t \, vs. \theta'(t)\) e \(\theta(t) \, vs. \theta'(t)\). O movimento parece periódico no tempo? (Use a hipótese de pequenos ângulos.)

