20. Ajuste de Curvas por Mínimos Quadrados

20.1. Regressão Linear

O exemplo mais simples de aproximação por mínimos quadrados é ajustar uma reta a um conjunto de pares de observações \((x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\). A expressão matemática do ajuste por uma reta é

\[ y = a_0 + a_1 x + e \qquad (1) \]

onde \(a_0\) e \(a_1\) são coeficientes representando a intersecção com o eixo \(y\) e a inclinação, respectivamente, e \(e\) é o erro ou resíduo entre o modelo e a observação, o qual pode ser representado, depois de se reorganizar a equação acima, por

\[ e = y − a_0 − a_1 x \]

Portanto, o erro ou resíduo é a discrepância entre o valor verdadeiro de \(y\) e o valor aproximado, \(a_0 + a_1 x\), previsto pela equação linear.

20.1.1. Critério para um Melhor Ajuste

Uma estratégia para ajustar uma melhor reta pelos dados é minimizar a soma dos quadrados dos resíduos entre o \(y\) medido e o \(y\) calculado com o modelo linear

\[ S_r = \sum _{i = 1}^{n} e_i^2 = \sum _{i = 1}^{n} (y_{i,medido} - y_{i,modelo})^2 = \sum _{i = 1}^{n} (y_i - a_0 - a_1 x_i)^2 \qquad (2) \]

Esse critério tem diversas vantagens, incluindo o fato de que ele fornece uma única reta para um dado conjunto de dados.

20.1.2. Ajuste por Mínimos Quadrados por uma Reta

Para determinar os valores de \(a_0\) e \(a_1\), a Equação (2) é derivada com relação a cada coeficiente

\[\begin{split} \dfrac{\partial S_r}{\partial a_0} = - 2 \sum (y_i - a_0 - a_1 x_i) \\ \dfrac{\partial S_r}{\partial a_1} = - 2 \sum [(y_i - a_0 - a_1 x_i) x_i] \end{split}\]

Igualando essas derivadas a zero será obtido um \(S_r\) mínimo

\[\begin{split} 0 = \sum y_i - \sum a_0 - \sum a_1 x_i \\ 0 = \sum y_i x_i - \sum a_0 x_i - \sum a_1 x_i^2 \end{split}\]

Agora, pode-se expressar essas equações como um conjunto de duas equações lineares simultâneas em duas variáveis (\(a_0\) e \(a_1\))

\[\begin{split} n a_0 + \left( \sum x_i \right) a_1 = \sum y_i \\ \left( \sum x_i \right) a_0 + \left( \sum x_i^2 \right) a_1 = \sum x_i y_i \end{split}\]

Essas são as chamadas equações normais. Elas podem ser resolvidas simultaneamente para obter-se

\[\begin{split} a_1 = \dfrac{n \sum x_i y_i - \sum x_i \sum y_i}{n \sum x_i^2 - (\sum x_i)^2} \qquad (3) \\ a_0 = \overline{y} - a_1 \overline{x} \qquad (4) \end{split}\]

onde \(\overline{y}\) e \(\overline{x}\) são as médias de \(y\) e \(x\), respectivamente.

20.1.3. Quantificação do Erro da Regressão Linear

Um “desvio padrão” para a reta de regressão pode ser determinado por

\[ s_{y/x} = \sqrt{\dfrac{S_r}{n-2}} \]

onde \(s_{y/x}\) é chamado erro padrão da estimativa. O subscrito “\(y/x\)” indica que o erro é para um valor previsto de \(y\) correspondente a um valor particular de \(x\). Além disso, observe que agora estamos dividindo por \(n − 2\) porque duas estimativas provenientes dos dados —\(a_0\) e \(a_1\) — foram usadas para calcular \(S_r\); portanto, perdemos dois graus de liberdade.

Exatamente como no caso do desvio padrão, o erro padrão da estimativa quantifica a dispersão dos dados. Entretanto, erro padrão da estimativa quantifica a dispersão em torno da reta de regressão, em contraste com o desvio padrão original que quantificava a dispersão em torno da média.

A fim de quantificar o “quão bom” é um ajuste de reta, dois conceitos utilizados são os coeficiente de determinação (\(r^2\)) e o coeficiente de correlação (\(r = \sqrt{r^2}\)).

\[ r^2 = \dfrac{S_t - S_r}{S_t} \]

\[ S_t = \sum _{i = 1}^n (y_i − \overline{y})^2 \]

Para um ajuste perfeito, \(S_r = 0\) e \(r = r_2 = 1\), significando que a reta explica 100% da variação dos dados. Para \(r = r_2 = 0\), \(S_r = St\) e o ajuste não representa nenhuma melhora. Uma formulação alternativa para \(r\) que é mais conveniente para implementação computacional é

\[ r = \dfrac{n \sum x_i y_i - (\sum x_i)(\sum y_i)}{\sqrt{n \sum x_i^2 - (\sum x_i)^2} \sqrt{n \sum y_i^2 - (\sum y_i)^2}} \qquad (5) \]

20.2. Regressão Polinomial

O procedimento dos mínimos quadrados pode ser prontamente estendido para ajustar dados por um polinômio de grau mais alto. Por exemplo, suponha que se queira ajustar um polinômio de segundo grau ou quadrático

\[ y = a_0 + a_1 x + a_2 x_2 + e \qquad (6) \]

Nesse caso, a soma dos quadrados dos resíduos é

\[ S_r = \sum _{i = 1}^n (y_i − a_0 − a_1 x_i − a_2 x_i^2)^2 \qquad (7) \]

Seguindo um procedimento análogo ao anterior, toma-se a derivada da Equação (7) com relação a cada um dos coeficientes desconhecidos do polinômio, como em

\[\begin{split} \dfrac{\partial S_r}{\partial a_0} = - 2 \sum (y_i - a_0 - a_1 x_i - a_2 x_i^2) \\ \dfrac{\partial S_r}{\partial a_1} = - 2 \sum [(y_i - a_0 - a_1 x_i - a_2 x_i^2) x_i] \\ \dfrac{\partial S_r}{\partial a_2} = - 2 \sum [(y_i - a_0 - a_1 x_i - a_2 x_i^2) x_i^2] \end{split}\]

Essas equações podem ser igualadas a zero e reorganizadas para determinar o seguinte conjunto de equações normais

\[\begin{split} n a_0 + \left( \sum x_i \right) a_1 + \left( \sum x_i^2 \right) a_2 = \sum y_i \\ \left( \sum x_i \right) a_0 + \left( \sum x_i^2 \right) a_1 + \left( \sum x_i^3 \right) a_2 = \sum x_i y_i \\ \left( \sum x_i^2 \right) a_0 + \left( \sum x_i^3 \right) a_1 + \left( \sum x_i^4 \right) a_2 = \sum x_i^2 y_i \end{split}\]

Nesse caso, vê-se que o problema de determinar o polinômio de segundo grau por mínimos quadrados é equivalente a resolver um sistema de três equações lineares simultâneas. Na forma matricial, temos

\[\begin{split} \begin{bmatrix} n & \sum x_i & \sum x_i^2 \\ \sum x_i & \sum x_i^2 & \sum x_i^3 \\ \sum x_i^2 & \sum x_i^3 & \sum x_i^4 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \\ \sum x_i^2 y_i \end{bmatrix} \qquad (8) \end{split}\]

O caso bidimensional pode ser facilmente estendido para um polinômio de grau \(m\).

\[ y = a_0 + a_1 x + a_2 x^2 + \dots + a_m x^m + e \]

20.3. Nota

O presente texto (conteúdo teórico) é um resumo baseado no livro Métodos Numéricos para Engenharia (Chapra e Canale).

20.4. Motivação: Evolução da População Paraibana

Este exemplo lê um arquivo CSV, plota o gráfico de dispersão, compara modelos e formata os dados para visualização.

import pandas as pd
from bokeh.io import output_notebook
from bokeh.plotting import figure, show
from bokeh.models import PrintfTickFormatter, Range1d

from scipy import stats
from scipy import interpolate

# tabela de dados
df = pd.read_csv("file-pop-pb.csv")
x = df['ano']
y = df['pop. urbana']

# grafico de dispersao
f = figure(plot_width=400, plot_height=400)
f.scatter(x,y,fill_color="blue",radius=1,alpha=1)

# formatacao
f.background_fill_color = "blue"
f.background_fill_alpha = 0.02
f.x_range=Range1d(1960, 2020)
e = 5.e5
f.y_range=Range1d(y.min() - e,y.max() + e)
f.xaxis.axis_label = "Ano"
f.yaxis.axis_label = "Pop. urbana - PB"
f.yaxis[0].formatter = PrintfTickFormatter(format="%1.2e")

# interpolacao

f.line(x,y,color='green')

# estimando o valor da populacao em 1975 e 1982 por interpolacao
p = interpolate.interp1d(x, y)

xx = [1975,1982]
yy = p(xx)
print("População obtida por interpolação linear em: 1975 = {:d}; 1982 = {:d}; ".format(int(yy[0]),int(yy[1])))
f.square(xx,yy,color='black',line_width=4)

# ajuste por minimos quadrados

slope, intercept, r_value, p_value, std_err = stats.linregress(x,y)
px = intercept + slope*x
f.line(x,px,color='red')

output_notebook()
show(f)

População obtida por interpolação linear em: 1975 = 1225580; 1982 = 1552017; 

Loading BokehJS ...

df.set_index('ano')

	pop. urbana
ano
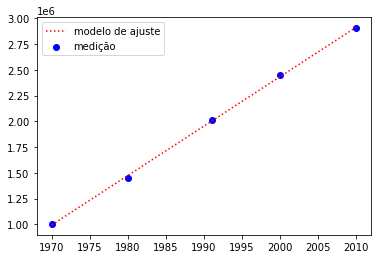
1970	1002156
1980	1449004
1991	2015576
2000	2447212
2010	2902044

20.5. Exemplo

Vamos resolver um problema de regressão linear por meio das equações normais passo a passo. Em primeiro lugar, importemos os módulos de computação numérica e de plotagem.

# importação de módulos 
import numpy as np
import matplotlib.pyplot as plt
import sympy as sy
%matplotlib inline

Consideremos a simples tabela abaixo de um experimento fictício que busca correlacionar densidade e diâmetro médio de grãos em alimentos.

densidade	diâmetro médio de grão
1.0	0.5
2.1	2.5
3.3	2.0
4.5	4.2

Vamos escrever os dados como arrays.

# tabela de dados
x = np.array([1,2,3,4]) # densidade
y = np.array([0.5,2.5,2.0,4.0]) # diâmetro

Agora, calculamos os coeficientes linear \(\alpha_0\) e angular \(\alpha_1\) pelas fórmulas das equações normais vistas em aula.

m = np.size(x)
alpha1 = (m*np.dot(x,y) - np.sum(x)*np.sum(y))/(m*np.dot(x,x)-np.sum(x)**2)
alpha0 = np.mean(y) - alpha1*np.mean(x)

Podemos agora escrever a equação da reta de regressão usando o array x como abscissa. Este será o nosso modelo de ajuste.

y2 = alpha0 + alpha1*x

Enfim, plotamos o gráfico de dispersão dos valores medidos juntamente com o modelo de ajuste da seguinte forma:

mod = plt.plot(x,y2,'r:'); # modelo
med = plt.scatter(x,y,c='b'); # medição
plt.legend({'modelo de ajuste':mod, 'medição':med}); # legenda
#plt.legend({'medição':med}); # legenda

# esta linha adiciona a equação de ajuste ao gráfico na posição (x,y) = (2.8,0.8)
# com fonte tamanho 14 e cor RGB = [0.4,0.5,0.4].
plt.annotate('y= {0:.2f} + {1:.2f}x'.format(alpha0,alpha1),(2.8,0.8),fontsize=14,c=[0.4,0.5,0.4]);

Na prática, podemos calcular regressão linear usando o módulo scipy.stats. Vide Code session 7.