21. Ajuste de curvas: caso não-linear

import numpy as np 
import matplotlib.pyplot as plt

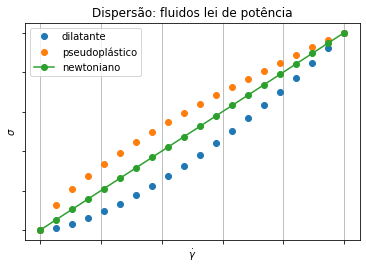
21.1. Motivação: comportamento de fluidos lei de potência

gamma = np.linspace(0,1,20,True)
n1 = 1.5 # dilatante
n2 = 0.7 # pseudoplastico
k = 0.1
tau1 = k*gamma**n1
tau2 = k*gamma**n2
tau3 = k*gamma

plt.plot(gamma,tau1,'o',label='dilatante')
plt.plot(gamma,tau2,'o',label='pseudoplástico')
plt.plot(gamma,tau3,'-o',label='newtoniano')
plt.legend()
plt.xlabel('$\dot{\gamma}$')
plt.ylabel('$\sigma}$')
plt.grid(axis='x')
plt.title('Dispersão: fluidos lei de potência')
plt.tick_params(axis='both',which='both',labelbottom=False,labelleft=False)

21.2. Exemplo

Determine os parâmetros \(a\) e \(b\) de modo que \(y = f(x) = ae^{bx}\) ajuste os seguintes dados no sentido de mínimos quadrados:

x	y
1.2	7.5
2.8	16.1
4.3	38.9
5.4	67.0
6.8	146.6
7.9	266.2

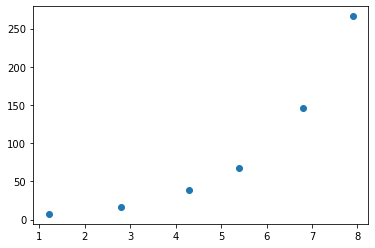
Plotando o gráfico de dispersão:

x = np.array([1.2,2.8,4.3,5.4,6.8,7.9])
y = np.array([7.5,16.1,38.9,67.0,146.6,266.2])
plt.plot(x,y,'o');

Teste de alinhamento: façamos a linearização

\[Y = Z + bx,\]

onde \(Y = \log(y)\) e \(Z = \log(a)\).

Plotemos a dispersão \((x,Y)\).

Y = np.log(y)
plt.plot(x,Y,'d');

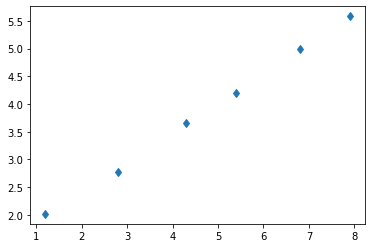
O teste do alinhamento nos diz que a função de ajuste é adequada para a regressão linear.

Regressão linear: façamos a regressão linear para buscar os parâmetros \(b\) e \(Z\) do modelo linearizado.

from scipy.stats import linregress

b,Z,R,p,e = linregress(x,Y)
print(f'Inclinação = {b:.3f}; offset = {Z:.3f}; R2 = {R*R:.3f}.')

Inclinação = 0.537; offset = 1.332; R2 = 0.999.

De fato, o coeficiente \(R^2 \approx 1.0\) mostra correlação quase máxima no modelo linearizado.

Comparação entre dados experimentais e ajustados: plotaremos agora a dispersão e o modelo ajustado.

a = np.exp(Z) # recupera o valor de a 
modelo = lambda x: a*np.exp(b*x)

plt.plot(x,y,'o',mfc='None')
plt.plot(x,modelo(x),'rs',mfc='None');
plt.legend(('amostras','ajuste'));

Estimando valores não tabelados: visto que o modelo exponencial se acomoda bem aos dados experimentais, agora podemos estimar valores que são desconhecidos, tais como \(x = 3.2\) ou \(x = 7.5\).

xp = np.array([3.2,7.5]) # valores procurados

for p in xp:
    print(f'Em x = {p:g}, a estimativa é f(x) = {modelo(p):g}')

Em x = 3.2, a estimativa é f(x) = 21.097
Em x = 7.5, a estimativa é f(x) = 211.969

21.2.1. Exercício

A seguinte tabela mostra a variação de condutividade térmica relativa \(k\) de sódio com a temperatura \(T\) em graus Celsius. Busque um modelo não-linear que ajusta os dados no sentido de mínimos quadrados.

k	T
1.00	79
0.932	190
0.839	357
0.759	524
0.693	690