25. Introdução à solução numérica de EDOs

Equações diferenciais ordinárias (EDOs) surgem em diversos problemas aplicados. Alguns exemplos:

• Química: decréscimo radioativo de carbono 14;

• Engenharia: queda da pressão atmosférica;

• Economia: precificação de ativos financeiros.

Nem sempre é possível obter soluções analíticas (forma fechada) para EDOs. Então, precisamos obter soluções aproximadas por meio de métodos numéricos.

No passado, muito esforço era empregado para se desenvolver métodos computacionais ótimos, mas a insuficiência de poder computacional era um entrave. Hoje em dia, com a evolução tecnológica, a capacidade computacional de alto desempenho permite que soluções numéricas sejam obtidas com menor esforço de processamento e margem de erro satisfatória. A seguir, faremos uma breve introdução teórica sobre modelos clássicos descritos por EDOs e a resolubilidade das equações.

25.1. Modelos clássicos

25.1.1. EDOs de primeira ordem

• Crescimento e decrescimento: modelo (de Malthus) utilizado em crescimento populacional, mor- talidade de espécies biológicas.

\[y'(t)=ky\Rightarrow y(t)=ce^{kt}, c,k \in \mathbb{R}\]

Interpretação: taxa de mudança da quantidade \(y\) é proporcional à própria quantidade ao longo do tempo. Se \(k > 0\), temos uma lei de crescimento; se \(k < 0\), temos uma lei de descrescimento (ou queda).

• Lei do resfriamento de Newton: modelo utilizado para determinar a troca de calor entre um corpo material e um meio externo.

\[T'(t) = k(T − T_{\infty}) \Rightarrow T(t) = T_0 + (T_{\infty} − T_0)e^{kt},\]

onde \(T\) é a temperatura do corpo, \(k > 0 \in \mathbb{R}\) a condutividade térmica (dependente do material do corpo e nem sempre constante), \(T_{\infty}\) a temperatura do ambiente e \(T_0\) a temperatura inicial.

Interpretação: taxa de mudança da temperatura é proporcional a diferença entre a temperatura do objeto e do ambiente com o qual troca calor.

25.1.2. EDOs de segunda ordem

• Variação da quantidade de movimento em um sistema (2a. lei de Newton): modelo utilizado para descrever a perda de equilíbrio de sistemas mecânicos (cordas vibrantes, molas amortecidas, escoamentos de fluidos viscosos).

\[my''(t) = −by'(t) − ky + f(t),\]

onde \(m\) é a massa, \(y\) é um deslocamento, \(t\) o tempo, b > 0 uma constante de amortecimento (absorvedor de choque), \(k > 0\) um parâmetro da mola/empuxo e \(f(t)\) uma força externa.

Interpretação: taxa de mudança da quantidade de movimento do corpo é igual às forças aplicadas sobre o mesmo. A solução geral desta equação não homogênea será omitida aqui (cf. Weiglholfer and Lindsay, p.32).

• 2a. lei de Kirchhoff: modelo usado em circuitos elétricos e eletromagnetismo.

\[LQ''(t) + RQ'(t) + \frac{1}{C}Q(t) = U(t),\]

onde \(Q(t)\) é a carga elétrica, \(L\) é a indutância, \(R\) a resistência, \(C\) a capacitância e \(U(t)\) a força eletromotora (tensão elétrica).

Interpretação: a força eletromotora (bateria, por exemplo) em qualquer circuito fechado equilibra todas as diferenças de potencial (d.d.p.) naquele circuito. Em outras palavras: em um circuito fechado, a soma de todas as d.d.p. é nula.

25.2. Teoria geral de resolubilidade de EDOs

25.2.1. Problema de Valor Inicial (PVI)

Um problema de valor inicial (PVI) é formado por uma EDO e uma condição inicial.

\[\begin{split}\begin{cases} y'(t) = f(t,y(t)) \\ y(t_0) = y_0 \end{cases},\end{split}\]

Acima, \(t\) é a variável independente, \(y(t)\) é a variável dependente (solução da EDO) e \(t_0\) é a condição inicial.

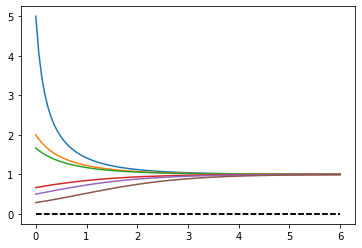
Exemplo: A EDO \(y'(t) = -[y(t)]^2 + y(t)\) possui a chamada solução trivial \(y(t) \equiv 0\) e a solução geral:

\[y(t) = \dfrac{1}{1+ce^{-t}}\]

Observemos que \(y(t)\) é indefinida quando \(1+ce^{-t}=0\), ou \(t = \ln(-c)\). Se \(y(0) = y_0 \neq 0\) for uma condição inicial geral, \(c = \frac{1}{y_0} - 1\) e teremos os seguintes resultados adicionais:

condição inicial	valores de \(c\)	existência de solução
\(y_0 > 0\)	\(c > -1\)	\(0 \leq t < \infty\)
\(y_0 < 0\)	\(c < -1\)	\(0 < t < \ln(1 - y_0^{-1})\)

Abaixo vemos os gráficos de \(Y(t)\) quando \(c = \{-0.8,-0.5,-0.4,0,0.5,1,0,2.5\}\) e para a solução trivial.

import numpy as np 
import matplotlib.pyplot as plt 

# variavel independente
t = np.linspace(0,6,100)

# condicao inicial
C = [-0.8,-0.5,-0.4,0,0.5,1,0,2.5]

for c in C:    

    # solucoes não triviais
    if c != 0:
        plt.plot(t,1./(1 + c*np.exp(-t)))
    
    # solucao trivial
    else:
        plt.plot(t,0*t,'k--')