27. Métodos de Taylor de Ordem Superior

Métodos que usam o desenvolvimento em série de Taylor de \(y(t)\) teoricamente fornecem solução para qualquer ED. Sob o ponto de vista computacional, Métodos de Taylor de ordem mais elevada são inaceitáveis, pois, exceto uma classe restrita de funções, o cálculo das derivadas totais é complicado.

Estes métodos são obtidos retendo-se termos de ordem superior na série de Taylor. Por sua vez, o Método de Euler é um caso particular, como veremos a seguir, já que tem os termos de ordem \(\geq 2\) truncados na série.

Suponhamos que \(y(t)\) a solução para o PVI \(\begin{cases} y' = f(t,y) \\ a \leq t \leq b \\ y(a) = \alpha \end{cases}\) é de classe \(\mathcal{C}^{n+1}\). Haja vista que a série de Taylor de \(y(t)\) em relação ao ponto \(t_i\) pode ser expandida até a ordem \(n\) como

\[\begin{equation*} y(t_{i+1}) = y(t_i) + {h} y'(t) + \frac{ {h}^2 }{2} y''(t_i) + \dots + \frac{ {h}^n }{n!} y^{(n)}(t_i) + \frac{ {h}^{n+1} }{(n+1)!} y^{(n+1)}(\xi_i), \end{equation*}\]

para \(\xi_i \in (t_i,t_{i+1})\).

A diferenciação sucessiva de \(y(t)\) fornece

\[\begin{align*} y'(t) &= f(t,y(t)) \\ y''(t) &= f'(t,y(t)) \\ & \vdots \\ y^k(t) &= f^{(k-1)}(t,y(t)) \end{align*}\]

Substituindo-as na série de Taylor, temos:

\[\begin{equation*} y(t_{i+1}) = y(t_i) + h f(t_i,y(t_i)) + \frac{ h^2 }{2} f'(t_i,y(t_i)) + \dots + \frac{ h^n }{n!} f^{(n-1)}(t_i,y(t_i)) + \frac{ h^{n+1} }{(n+1)!} f^{(n)}(\xi_i,y(\xi_i)) \end{equation*}\]

Excluindo o termo de resto envolvendo \(\xi\), obtemos o Método de Taylor de ordem \(n\) através do seguinte processo iterativo

\[\begin{align*} w_0 &= \alpha \\ w_{i+1} &= w_i + T^{(n)}(t_i,w_i), \quad i = 0,1,2, \ldots, N \end{align*}\]

em que

\[T^{(n)}(t_i,w_i) = f(t_i,w_i) + \frac{h}{2} f'(t_i,y(t_i)) + \dots + \frac{ h^{n-1} }{n!}f^{(n-1)}(t_i,w_i).\]

Logo, vemos que o método de Euler é o Método de Taylor de ordem 1. As derivadas sucessivas podem ser calculadas pela Regra da Cadeia. Por exemplo,

\[y' = f(t,y) \Rightarrow y'' = f_t(t,y) + f_y(t,y) y' = f_t(t,y) + f_y(t,y) f(t,y).\]

Todavia, os métodos da família Runge-Kutta são alternativas numéricas melhores para métodos de Taylor pois simulam o efeito das derivadas a partir de cálculos médios que não necessitam de derivadas analíticas. Estudaremos métodos de Runge-Kutta em breve.

Exemplo: Aplique o Método de Taylor de ordem 2 ao PVI

\[\begin{split}\begin{cases} y'= y − t^2 + 1 \\ 0 \leq t \leq 2 \\ y(0) = 0.5. \end{cases}\end{split}\]

Para o método de ordem 2, precisamos da primeira derivada de \(f(t,y(t)) = y(t) − t^2 + 1\) em relação a \(t\). Então,

\[f'(t,y(t)) = \frac{d}{dt} (y − t^2 + 1) = y' − 2t = (y − t^2 + 1) − 2t,\]

de modo que

\[\begin{split}T^{(2)}(t_i,w_i) = f(t_i,w_i)+ \frac{h}{2}f'(t_i,w_i) = w_i − t_i^2 + 1 + \frac{h}{2}(w_i − t_i^2 + 1 − 2t_i) = \\ = \left( 1 + \frac{h}{2} \right) (w_i − t_i^2 + 1) − ht_i\end{split}\]

Como \(N = 10\), temos \(h = 0.2\) e \(t_i = 0.2i, \forall i = 1,2,...,10\). Assim, o método de segunda ordem torna-se

\[\begin{split}w_0 = 0.5 \\ w_{i+1} = w_i + h \left[ \left(1 + \frac{h}{2} \right)(w_i − t_i^2 + 1) − h t_i \right] = \\ = w_i + 0.2 \left[ \left(1 + \frac{0.2}{2} \right) (w_i − 0.04i^2 + 1) −0.04i \right] \\ = 1.22w_i − 0.0088i^2 − 0.008i + 0.22.\end{split}\]

Os dois primeiros passos dão a aproximação:

\[y(0.2) \approx w_1 = 1.22(0.5) − 0.0088(0)^2 − 0.008(0) + 0.22 = 0.83\]

\[y(0.4) \approx w_2 = 1.22(0.83) − 0.0088(0.2)^2 − 0.008(0.2) + 0.22 = 1.2158\]

\[(\ldots)\]

Os demais passos seguem da mesma forma

27.1. Métodos de Runge-Kutta

O objetivo principal dos métodos de Runge-Kutta (RK) é imitar o comportamento de \(f(t,y)\) avaliando-a em vários pontos “abstratos” dentro de um mesmo passo numérico.

Esquemas do tipo RK são usados para reter precisão e substituir aproximações de baixa ou alta ordem via séries de Taylor. São populares na resolução de PVIs e mais simples de programar do que os métodos de Taylor.

27.1.1. Forma geral

A forma geral de um método RK é dada por:

\[\begin{split}\begin{cases} w_{n+1} &=& w_n + hF(t_n,w_n;h), \ \ n \geq 0 \\ w_0 &=& y_0 \end{cases}\end{split}\]

O termo \(F(t_n,w_n;h)\) representa uma inclinação média, de maneira que, informalmente, métodos RK seja refraseados como:

valor futuro = valor atual + passo x inclinação média.

Se fizéssemos uma analogia com o movimento uniforme da física, \(w\) seria uma posição do espaço, \(h\) o tempo e \(F\) a velocidade, resultando em

posição final = posição inicial + tempo x velocidade

ou, equivalentemente, \(s_f = s_0 + vt\).

27.1.2. Métodos de Runge-Kutta de 2a. ordem

Para métodos RK2, a inclinação média é dada pela expressão

\[F(t,w;h) = b_1 f(t,w) + b_2 f(t+\alpha h, w + \beta h f(t,w),\]

em que \(\alpha, \beta, b_1, b_2 \in \mathbb{R}\) são constantes a serem determinadas de modo que atinjamos um erro de truncamento

\[T_{n+1}(w) = w_{n+1} - [ w_n + h F(t_n,w_n;h) ] \equiv \mathcal{O}(h^3),\]

i.e., seja de terceira ordem.

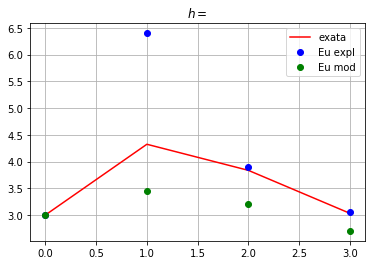
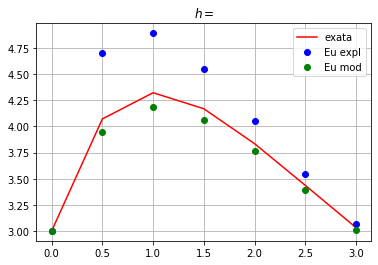
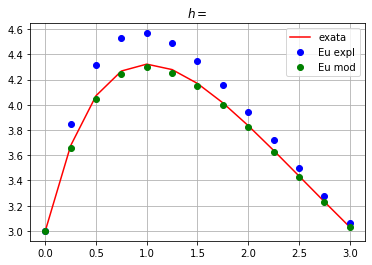
Abaixo, vamos resolver o PVI:

\begin{cases} y’ = -1.2y + 7e^(-0.3x) \ y(0) = 3 \ 0 < x \leq 2 \ h = 1,0.5,0.25,0.1 \end{cases}

# definição
e = np.exp(1)

# dados de entrada 
a = 0
b = 3.0
ns = [4,7,13,31]
w0 = 3
ode = '-1.2*y + 7*e**(-0.3*x)'

# soluções numéricas

for n in ns:
    # MEE
    x,we = ode_euler_expl(ode,a,b,n,w0)

    # MEM
    x,wm = ode_euler_mod(ode,a,b,n,w0)

    # conversao de dados
    x = np.asarray(x)
    we = np.asarray(we)
    wm = np.asarray(wm)

    # solução exata
    y = 70/9*e**(-0.3*x) - 43/9*e**(-1.2*x)

    # curvas
    plt.figure()
    plt.plot(x,y,'r',label='exata')
    plt.plot(x,we,'bo',label='Eu expl')
    plt.plot(x,wm,'go',label='Eu mod')
    plt.legend()
    tit = '$h = ' + str((b-a)/(n-1)) + '$'
    plt.title('$h=$')
    plt.grid()