Lista de Exercícios 3
Contents
Lista de Exercícios 3#
Solucionário matemático e computacional de exercícios selecionados da Lista de Exercícios 3.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# Funções Implementadas
def gauss_simples(AB):
'''Realiza o cálculo de um sistema linear através do método de eliminação de Gauss sem pivotamento.
Sinopse:
X = gauss_simples(AB)
Entradas:
AB - Matriz aumentada (np.array) do sistema linear
Saídas:
X - Vetor solução do sistema linear
@ney
'''
# Eliminação progressiva de variáveis
for i in range(len(AB)):
for j in range(len(AB)):
if (j > i):
m = AB[j,i]/AB[i,i] # Fator multiplicador
AB[j,:] -= m*AB[i,:] # Eliminação de variável
# Substituição regressiva
A = AB[:,0:-1]
B = AB[:,-1]
X = np.zeros((len(AB),1))
for i in range(len(A)-1, -1, -1):
for j in range(len(A)):
X[i] -= A[i,j]*X[j]
X[i] += B[i]
X[i] /= A[i,i]
X = np.around(X, decimals=3)
return X
def gauss_pivparc(AB):
'''Realiza o cálculo de um sistema linear através do método de eliminação de Gauss com pivotamento parcial.
Sinopse:
X = gauss_pivparc(AB)
Entradas:
AB - Matriz aumentada (np.array) do sistema linear
Saídas:
X - Vetor solução do sistema linear
@ney
'''
# Eliminação progressiva de variáveis
for i in range(len(AB)):
if (i < len(AB)): # Pivotamento parcial
AB_new = np.flip(AB[i:, i:], 0)
AB[i:, i:] = AB_new
for j in range(len(AB)):
if (j > i):
m = AB[j,i]/AB[i,i] # Fator multiplicador
AB[j,:] -= m*AB[i,:] # Eliminação de variável
# Substituição regressiva
A = AB[:,0:-1]
B = AB[:,-1]
X = np.zeros((len(AB),1))
for i in range(len(A)-1, -1, -1):
for j in range(len(A)):
X[i] -= A[i,j]*X[j]
X[i] += B[i]
X[i] /= A[i,i]
X = np.around(X, decimals=3)
return X
def gaussjordan(AB):
'''Realiza o cálculo de um sistema linear através do método de eliminação de Gauss-Jordan simples.
Sinopse:
X = gaussjordan(AB)
Entradas:
AB - Matriz aumentada (np.array) do sistema linear
Saídas:
X - Vetor solução do sistema linear
@ney
'''
for i in range(len(AB)):
AB[i,:] /= AB[i,i]
for j in range(len(AB)):
if (j != i):
AB[j,:] -= AB[j,i]*AB[i,:]
AB = np.around(AB, decimals=3)
return AB[:,-1]
def lu_solver(AB):
'''Realiza o cálculo de um sistema linear através do método de decomposição LU.
Sinopse:
L, U, X = lu_solver(AB)
Entradas:
AB - Matriz aumentada (np.array) do sistema linear
Saídas:
L (lu[0]) - Matriz triangular inferior
U (lu[1]) - Matriz triangular superior
X (lu[2]) - Vetor solução do sistema linear
@ney
'''
# Decomposição LU
U = np.copy(AB)
U = U[:,0:-1]
L = np.zeros((len(AB),len(AB)))
for i in range(len(AB)):
for j in range(len(AB)):
if (j > i):
m = U[j,i]/U[i,i]
U[j,:] -= m*U[i,:]
L[j,i] = m
elif (j == i):
L[i,i] = 1
# Substituição progressiva
B = np.copy(AB)
B = B[:,-1]
D = np.zeros((len(AB),1))
for i in range(len(L)):
for j in range(len(L)):
if (i > j):
D[i] -= L[i,j]*D[j]
D[i] += B[i]
# Substituição regressiva
X = np.zeros((len(AB),1))
for i in range(len(U)-1, -1, -1):
for j in range(len(U)):
X[i] -= U[i,j]*X[j]
X[i] += D[i]
X[i] /= U[i,i]
L = np.around(L, decimals=3)
U = np.around(U, decimals=3)
X = np.around(X, decimals=3)
return (L, U, X)
def cholesky(AB):
'''Realiza o cálculo de um sistema linear através do método LU, por decomposição de Cholesky.
Sinopse:
C = cholesky(AB)
Entradas:
AB - Matriz aumentada (np.array) do sistema linear
Saídas:
G (C[0]) - Matriz triangular inferior
X (C[1]) - Vetor solução do sistema linear
@ney
'''
# Decomposição de Cholesky
A = np.copy(AB)
A = A[:,0:-1]
G = np.zeros((len(A),len(A)))
for k in range(len(A)):
for i in range(k):
s1 = 0
for j in range(i):
s1 += G[i,j]*G[k,j]
G[k,i] = (A[k,i] - s1)/G[i,i]
s2 = 0
for j in range(k):
s2 += (G[k,j])**2
G[k,k] = np.sqrt(A[k,k] - s2)
# Substituição progressiva
B = np.copy(AB)
B = B[:,-1]
D = np.zeros((len(AB),1))
for i in range(len(G)):
for j in range(len(G)):
if (i > j):
D[i] -= G[i,j]*D[j]
D[i] += B[i]
D[i] /= G[i,i]
# Substituição regressiva
GT = G.transpose()
X = np.zeros((len(AB),1))
for i in range(len(GT)-1, -1, -1):
for j in range(len(GT)):
X[i] -= GT[i,j]*X[j]
X[i] += D[i]
X[i] /= GT[i,i]
G = np.around(G, decimals=3)
X = np.around(X, decimals=3)
return G,X
Sistemas lineares#
Questão 1#
Escreva o seguinte conjunto de equações na forma matricial:
(1)#\[\begin{align}
8 &= 6x_3 + 2x_2 \\
2 − x_1 &= x_3 \\
5x_2 + x_1 &= 13
\end{align}\]
Mulitiplique a matriz dos coeficientes por sua transposta, i.e. \(AA^T\).
# Solução
A = np.array([[0, 2, 6], [1, 0, 1], [1, 5, 0]])
AT = A.transpose()
B = np.dot(A,AT)
print("A matriz dos coeficientes desse sistema é: \n\n", A)
print("\nA sua transposta é: \n\n", AT)
print("\nLogo, o produto entre A e sua transposta é: \n\n", B)
A matriz dos coeficientes desse sistema é:
[[0 2 6]
[1 0 1]
[1 5 0]]
A sua transposta é:
[[0 1 1]
[2 0 5]
[6 1 0]]
Logo, o produto entre A e sua transposta é:
[[40 6 10]
[ 6 2 1]
[10 1 26]]
Questão 2#
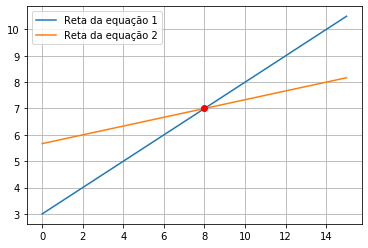
Use o metodo gráfico para resolver:
(2)#\[\begin{align}
4x_1 − 8x_2 &= −24 \\
−x_1 + 6x_2 &= 34
\end{align}\]
# Solução
def f1(x):
return (4*x + 24)/8 # x2 isolado na primeira equação
def f2(x):
return (x + 34)/6 # x2 isolado na segunda equação
x1 = np.linspace(0, 15, 100)
y1 = f1(x1) # Valores de x2 na primeira equação
y2 = f2(x1) # Valores de x2 na segunda equação
plt.plot(x1,y1, label="Reta da equação 1")
plt.plot(x1,y2, label="Reta da equação 2")
plt.grid()
plt.legend()
plt.plot(8,7,'or')
[<matplotlib.lines.Line2D at 0x7f84f958d8d0>]
Questão 3#
Para o conjunto de equações:
(3)#\[\begin{align}
2x_2 + 5x_3 &= 9 \\
2x_1 + x_2 + x_3 &= 9 \\
3x_1 + x_2 &= 10
\end{align}\]
(i) Calcule o determinante.
(ii) Use a regra de Cramer para determinar \(x_1\), \(x_2\), \(x_3\).
# Solução
# (i)
A = np.array([[0, 2, 5], [2, 1, 1], [3, 1, 0]])
det = np.linalg.det(A)
print("(i) det(A) = ", det)
# (ii)
A = tuple(A)
B = np.array([[9], [9], [10]])
X = []
for coluna in range(len(A)):
C = np.asarray(A)
for linha in range(len(A)):
C[linha][coluna] = B[linha]
X.append(np.linalg.det(C)/np.linalg.det(np.asarray(A)))
X = [round(i,3) for i in X]
print("\n(ii) Os valores de [x1, x2, x3] são:", X)
(i) det(A) = 0.9999999999999991
(ii) Os valores de [x1, x2, x3] são: [6.0, -8.0, 5.0]
Questão 4#
Dadas as equações:
(4)#\[\begin{align}
10x_1 + 2x_2 − x_3 &= 27 \\
−3x_1 − 6x_2 + 2x_3 &= −61.5 \\
x_1 + 5x_2 + 5x_3 &= −21.5
\end{align}\]
Resolva por Eliminação de Gauss Simples. Mostre todos os passos de cálculo.
# Solução
AB = np.array([[10., 2., -1., 27], [-3., -6., 2., 61.5], [1., 5., 5., -21.5]])
# Eliminação progressiva de variáveis
f = 0;
for i in range(len(AB)):
for j in range(len(AB)):
if (j > i):
m = AB[j,i]/AB[i,i] # Fator multiplicador
f += 1
print("\nO fator multiplicativo", f, "é:", m)
AB[j,:] -= m*AB[i,:] # Eliminação de variável
print("Após a eliminação de variável, temos:\n", AB)
# Substituição regressiva
A = AB[:,0:-1]
B = AB[:,-1]
X = np.zeros((3,1))
for i in range(len(A)-1, -1, -1):
for j in range(len(A)):
X[i] -= A[i,j]*X[j]
X[i] += B[i]
X[i] /= A[i,i]
X = np.around(X, decimals=3)
print("\nA solução do problema é: \n", X)
O fator multiplicativo 1 é: -0.3
Após a eliminação de variável, temos:
[[ 10. 2. -1. 27. ]
[ 0. -5.4 1.7 69.6]
[ 1. 5. 5. -21.5]]
O fator multiplicativo 2 é: 0.1
Após a eliminação de variável, temos:
[[ 10. 2. -1. 27. ]
[ 0. -5.4 1.7 69.6]
[ 0. 4.8 5.1 -24.2]]
O fator multiplicativo 3 é: -0.8888888888888888
Após a eliminação de variável, temos:
[[10. 2. -1. 27. ]
[ 0. -5.4 1.7 69.6 ]
[ 0. 0. 6.61111111 37.66666667]]
A solução do problema é:
[[ 5.489]
[-11.095]
[ 5.697]]
Questão 5#
Use Eliminação de Gauss com pivotamento parcial para resolver:
(5)#\[\begin{align}
8x_1 + 2x_2 − 2x_3 &= −2 \\
10x_1 + 2x_2 − 4x_3 &= 4 \\
12x_1 + 2x_2 + 2x_3 &= 6
\end{align}\]
# Solução
AB = np.array([[8., 2., -2., -2], [10., 2., -4., 4], [12., 2., 2., 6]])
X = gauss_pivparc(AB)
print("A solução do problema é: \n", X)
A solução do problema é:
[[ 2.5]
[-11.5]
[ -0.5]]
Questão 6#
Dadas as equações:
(6)#\[\begin{align}
2x_1 − 6x_2 − x_3 &= −38 \\
−3x_1 − x_2 + 7x_3 &= 34 \\
−8x_1 + x_2 − 2x_3 &= −20
\end{align}\]
Resolva por Eliminação de Gauss com pivotamento parcial.
# Solução
AB = np.array([[2., -6., -1., -38], [-3., -1., 7., 34], [-8., 1., -2., -20]])
X = gauss_pivparc(AB)
print("A solução do problema é: \n", X)
A solução do problema é:
[[1.63 ]
[5.812]
[6.386]]
Questão 7#
Use Eliminação de Gauss-Jordan para resolver:
(7)#\[\begin{align}
2x_1 + x_2 − x_3 &= 1 \\
5x_1 + 2x_2 + 2x_3 &= −4 \\
3x_1 + x_2 + x_3 &= 5
\end{align}\]
Não utilize pivotamento. Substitua seus resultados nas equações originais para verificá-los.
# Solução
AB = np.array([[2., 1., -1., 1], [5., 2., 2., -4], [3., 1., 1., 5]])
X = gaussjordan(AB)
print("A solução do problema é", X)
A solução do problema é [ 14. -32. -5.]
Questão 8#
Resolva:
(8)#\[\begin{align}
x_1 + x_2 − x_3 &= −3 \\
6x_1 + 2x_2 + 2x_3 &= 2 \\
−3x_1 + 4x_2 + x_3 &= 1
\end{align}\]
(i) Por Eliminação de Gauss simples.
(ii) Por Eliminação de Gauss com pivotamento parcial.
(iii) Por Eliminação de Gauss-Jordan sem pivotamento parcial.
# Solução
# (i) Eliminação de Gauss simples
AB = np.array([[1., 1., -1., -3], [6., 2., 2., 2], [-3., 4., 1., 1]])
X = gauss_simples(AB)
print("(i) A solução do problema, pelo método da eliminação de Gauss simples, é: \n", X)
# (ii) Eliminação de Gauss com pivotamento parcial
AB = np.array([[1., 1., -1., -3], [6., 2., 2., 2], [-3., 4., 1., 1]])
X = gauss_pivparc(AB)
print("\n(ii) A solução do problema, pelo método da eliminação de Gauss com pivotamento parcial, é: \n", X)
# (iii) Eliminação de Gauss-Jordan sem pivotamento parcial
AB = np.array([[1., 1., -1., -3], [6., 2., 2., 2], [-3., 4., 1., 1]])
X = gaussjordan(AB)
print("\n(ii) A solução do problema, pelo método da eliminação de Gauss-Jordan sem pivotamento parcial, é: \n", AB[:,-1])
(i) A solução do problema, pelo método da eliminação de Gauss simples, é:
[[-0.25]
[-0.5 ]
[ 2.25]]
(ii) A solução do problema, pelo método da eliminação de Gauss com pivotamento parcial, é:
[[-0.25]
[-0.5 ]
[ 2.25]]
(ii) A solução do problema, pelo método da eliminação de Gauss-Jordan sem pivotamento parcial, é:
[-0.25 -0.5 2.25]
Fatoração LU#
Questão 9#
Resolva o seguinte sistema de equações por decomposição LU sem pivotamento (usando a definição A = LU):
(9)#\[\begin{align}
8x_1 + 4x_2 − x_3 &= 11 \\
−2x_1 + 5x_2 + x_3 &= 4 \\
2x_1 − x_2 + 6x_3 &= 7
\end{align}\]
Em seguida, determine a matriz inversa \(A^{−1} = U^{−1} L^{−1}\). Verifique seus resultados comprovando que \(AA^{−1} = I\).
#Solução
AB = np.array([[8., 4., -1., 11.], [-2., 5., 1., 4.], [2., -1., 6., 7.]])
L, U, X = lu_solver(AB)
A = np.copy(AB)
A = A[:,0:-1]
print("A solução do sistema é: \n", X)
print("\nA inversa de A é: \n", np.around(np.linalg.inv(A), decimals=3))
print("\nO produto entre as inversas de U e L é: \n", np.around(np.dot(np.linalg.inv(U),np.linalg.inv(L)), decimals=3))
print("\nO produto entre A e sua inversa é: \n", np.around(np.dot(A,np.linalg.inv(A))))
A solução do sistema é:
[[1.]
[1.]
[1.]]
A inversa de A é:
[[ 0.099 -0.074 0.029]
[ 0.045 0.16 -0.019]
[-0.026 0.051 0.154]]
O produto entre as inversas de U e L é:
[[ 0.099 -0.074 0.029]
[ 0.045 0.16 -0.019]
[-0.026 0.051 0.154]]
O produto entre A e sua inversa é:
[[ 1. 0. 0.]
[-0. 1. 0.]
[-0. 0. 1.]]
Questão 10#
Resolva o seguinte sistema de equações por decomposição LU com pivotamento parcial.
(10)#\[\begin{align}
2x_1 − 6x_2 − x_3 &= −38 \\
−3x_1 − x_2 + 7x_3 &= −34 \\
−8x_1 + x_2 − 2x_3 &= −20
\end{align}\]
Em seguida, determine a matriz inversa \(A^{−1} = U^{−1} L^{−1}\). Verifique seus resultados comprovando que \(AA^{−1} = I\).
#Solução
AB = np.array([[2., -6., -1., -38.], [-3., -1., 7., -34.], [-8., 1., -2., -20.]])
L, U, X = lu_solver(AB)
A = np.copy(AB)
A = A[:,0:-1]
print("A matriz L é: \n", L)
print("\nA matriz U é: \n", U)
print("\nA solução do sistema é: \n", X)
print("\nA inversa de A é: \n", np.around(np.linalg.inv(A), decimals=3))
print("\nO produto entre as inversas de U e L é: \n", np.around(np.dot(np.linalg.inv(U),np.linalg.inv(L)), decimals=3))
print("\nO produto entre A e sua inversa é: \n", np.around(np.dot(A,np.linalg.inv(A))))
A matriz L é:
[[ 1. 0. 0. ]
[-1.5 1. 0. ]
[-4. 2.3 1. ]]
A matriz U é:
[[ 2. -6. -1. ]
[ 0. -10. 5.5 ]
[ 0. 0. -18.65]]
A solução do sistema é:
[[ 4.]
[ 8.]
[-2.]]
A inversa de A é:
[[-0.013 -0.035 -0.115]
[-0.166 -0.032 -0.029]
[-0.029 0.123 -0.054]]
O produto entre as inversas de U e L é:
[[-0.013 -0.035 -0.115]
[-0.166 -0.032 -0.029]
[-0.029 0.123 -0.054]]
O produto entre A e sua inversa é:
[[ 1. -0. -0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
Questão 11#
Resolva o seguinte sistema de equações por decomposição LU.
(11)#\[\begin{align}
10x_1 + 2x_2 − x_3 &= 27 \\
−3x_1 − 6x_2 + 2x_3 &= −61.5 \\
x_1 + x_2 + 5x_3 &= −21.5
\end{align}\]
Em seguida, determine a matriz inversa \(A^{−1} = U^{−1} L^{−1}\). Verifique seus resultados comprovando que \(AA^{−1} = I\).
#Solução
AB = np.array([[10., 2., -1., 27.], [-3., -6., 2., -61.5], [1., 1., 5., -21.5]])
L, U, X = lu_solver(AB)
A = np.copy(AB)
A = A[:,0:-1]
print("A matriz L é: \n", L)
print("\nA matriz U é: \n", U)
print("\nA solução do sistema é: \n", X)
print("\nA inversa de A é: \n", np.around(np.linalg.inv(A), decimals=3))
print("\nO produto entre as inversas de U e L é: \n", np.around(np.dot(np.linalg.inv(U),np.linalg.inv(L)), decimals=3))
print("\nO produto entre A e sua inversa é: \n", np.around(np.dot(A,np.linalg.inv(A))))
A matriz L é:
[[ 1. 0. 0. ]
[-0.3 1. 0. ]
[ 0.1 -0.148 1. ]]
A matriz U é:
[[10. 2. -1. ]
[ 0. -5.4 1.7 ]
[ 0. 0. 5.352]]
A solução do sistema é:
[[ 0.5]
[ 8. ]
[-6. ]]
A inversa de A é:
[[ 0.111 0.038 0.007]
[-0.059 -0.176 0.059]
[-0.01 0.028 0.187]]
O produto entre as inversas de U e L é:
[[ 0.111 0.038 0.007]
[-0.059 -0.176 0.059]
[-0.01 0.028 0.187]]
O produto entre A e sua inversa é:
[[ 1. -0. 0.]
[ 0. 1. 0.]
[-0. -0. 1.]]
Fatoração de Cholesky#
Questão 12#
Determine quais matrizes a seguir são (i) simétricas, (ii) singulares, (iii) diagonalmente dominantes, (iv) positivas definidas.
(a) \begin{pmatrix} 2 & 1 \ 1 & 3 \end{pmatrix}
(b) \begin{pmatrix} 2 & 1 & 0 \ 0 & 3 & 0 \ 1 & 0 & 4 \end{pmatrix}
© \begin{pmatrix} 4 & 2 & 6 \ 3 & 0 & 7 \ -2 & -1 & -3 \end{pmatrix}
(d) \begin{pmatrix} 4 & 0 & 0 & 0 \ 6 & 7 & 0 & 0 \ 9 & 11 & 1 & 0 \ 5 & 4 & 1 & 1 \end{pmatrix}
# Solução
A = np.array([[2., 1.], [1., 3.]])
B = np.array([[2., 1., 0.], [0., 3., 0.], [1., 0., 4.]])
C = np.array([[4., 2., 6.], [3., 0., 7.], [-2., -1., -3.]])
D = np.array([[4., 0., 0., 0.], [6., 7., 0., 0.], [9., 11., 1., 0.], [5., 4., 1., 1.]])
menA = []
for i in range(1,len(A)+1):
menA.append(np.linalg.det(A[0:i, 0:i]))
print("Os determinantes dos menores principais de (a) são:", np.around(menA, decimals=3))
menB = []
for i in range(1,len(B)+1):
menB.append(np.linalg.det(B[0:i, 0:i]))
print("\nOs determinantes dos menores principais de (b) são:", np.around(menB, decimals=3))
menC = []
for i in range(1,len(C)+1):
menC.append(np.linalg.det(C[0:i, 0:i]))
print("\nOs determinantes dos menores principais de (c) são:", np.around(menC, decimals=3))
menD = []
for i in range(1,len(D)+1):
menD.append(np.linalg.det(D[0:i, 0:i]))
print("\nOs determinantes dos menores principais de (d) são:", np.around(menD, decimals=3))
Os determinantes dos menores principais de (a) são: [2. 5.]
Os determinantes dos menores principais de (b) são: [ 2. 6. 24.]
Os determinantes dos menores principais de (c) são: [ 4. -6. 0.]
Os determinantes dos menores principais de (d) são: [ 4. 28. 28. 28.]
Solução:#
(i) Apenas a matriz em (a) e simétrica.
(ii) Apenas a matriz em (d) é singular.
(iii) As matrizes em (a) e (b) são diagonalmente dominantes.
(iv) As matrizes em (a), (b) e (d) são positivas-definidas.
Questão 13#
Determine a fatoração de Cholesky \(A = GGT\) das matrizes a seguir.
(a) \begin{pmatrix} 2 & −1 & 0 \ −1 & 2 & −1 \ 0 & −1 & 2 \end{pmatrix}
(b) \begin{pmatrix} 4 & 1 & 1 & 1 \ 1 & 3 & −1 & 1 \ 1 & −1 & 2 & 0 \ 1 & 1 & 0 & 2 \end{pmatrix}
© \begin{pmatrix} 4 & 1 & −1 & 0 \ 1 & 3 & −1 & 0 \ −1 & −1 & 5 & 2 \ 0 & 0 & 2 & 4 \end{pmatrix}
# Solução
# (a)
print("(a)")
A = np.array([[2., -1., 0.], [-1., 2., -1.], [0., -1., 2.]])
G = np.zeros((len(A),len(A)))
for k in range(len(A)):
for i in range(k):
s1 = 0
for j in range(i):
s1 += G[i,j]*G[k,j]
G[k,i] = (A[k,i] - s1)/G[i,i]
s2 = 0
for j in range(k):
s2 += (G[k,j])**2
G[k,k] = np.sqrt(A[k,k] - s2)
G = np.around(G, decimals=3)
print("A matriz G é:\n", G)
# (b)
print("\n(b)")
B = np.array([[4., 1., 1., 1.], [1., 3., -1., 1.], [1., -1., 2., 0.], [1., 1., 0., 2.]])
G = np.zeros((len(B),len(B)))
for k in range(len(B)):
for i in range(k):
s1 = 0
for j in range(i):
s1 += G[i,j]*G[k,j]
G[k,i] = (B[k,i] - s1)/G[i,i]
s2 = 0
for j in range(k):
s2 += (G[k,j])**2
G[k,k] = np.sqrt(B[k,k] - s2)
G = np.around(G, decimals=3)
print("A matriz G é:\n", G)
# (c)
print("\n(c)")
C = np.array([[4., 1., -1., 0.], [1., 3., -1., 0.], [-1., -1., 5., 2.], [0., 0., 2., 4.]])
G = np.zeros((len(C),len(C)))
for k in range(len(C)):
for i in range(k):
s1 = 0
for j in range(i):
s1 += G[i,j]*G[k,j]
G[k,i] = (C[k,i] - s1)/G[i,i]
s2 = 0
for j in range(k):
s2 += (G[k,j])**2
G[k,k] = np.sqrt(C[k,k] - s2)
G = np.around(G, decimals=3)
print("A matriz G é:\n", G)
(a)
A matriz G é:
[[ 1.414 0. 0. ]
[-0.707 1.225 0. ]
[ 0. -0.816 1.155]]
(b)
A matriz G é:
[[ 2. 0. 0. 0. ]
[ 0.5 1.658 0. 0. ]
[ 0.5 -0.754 1.087 0. ]
[ 0.5 0.452 0.084 1.24 ]]
(c)
A matriz G é:
[[ 2. 0. 0. 0. ]
[ 0.5 1.658 0. 0. ]
[-0.5 -0.452 2.132 0. ]
[ 0. 0. 0.938 1.766]]
Questão 14#
Resolva os seguintes sistemas de equações por decomposição de Cholesky.
(a) \begin{cases} 8x_1 + 20x_2 + 15x_3 = 50 \ 20x_1 + 80x_2 + 50x_3 = 250 \ 15x_1 + 50x_2 + 60x_3 = 100 \end{cases}
(b) \begin{cases} 6x_1 + 15x_2 + 55x_3 = 152.6 \ 15x_1 + 55x_2 + 225x_3 = 585.6 \ 55x_1 + 225x_2 + 979x_3 = 2488.8 \end{cases}
© \begin{cases} 2x_1 − x_2 = 3 \ −x_1 + 2x_2 − x_3 = − 3 \ −x_2 + 2x_3 = 1 \end{cases}
(d) \begin{cases} 4x_1 + x_2 + x_3 + x_4 = 0.65 \ x_1 + 3x_2 − x_3 + x_4 = 0.05 \ x_1 − x_2 + 2x_3 = 0 \ x_1 + x_2 + 2x_4 = 0.5 \end{cases}
# Solução
# (a)
print("(a)")
AB = np.array([[8., 20., 15., 50.], [20., 80., 50., 250.], [15., 50., 60., 100.]])
G, X = cholesky(AB)
print("A solução do sistema é: \n", G)
# (b)
print("\n(b)")
AB = np.array([[6., 15., 55., 152.6], [15., 55., 225., 585.6], [55., 225., 979., 2488.8]])
G, X = cholesky(AB)
print("A solução do sistema é: \n", G)
# (c)
print("\n(c)")
AB = np.array([[2., -1., 0., 3.], [-1., 2., -1., -3.], [0., -1., 2., 1.]])
G, X = cholesky(AB)
print("A solução do sistema é: \n", G)
# (d)
print("\n(d)")
AB = np.array([[4., 1., 1., 1., 0.65], [1., 3., -1., 1., 0.05], [1., -1., 2., 0., 0.], [1., 1., 0., 2., 0.5]])
G, X = cholesky(AB)
print("A solução do sistema é: \n", G)
(a)
A solução do sistema é:
[[2.828 0. 0. ]
[7.071 5.477 0. ]
[5.303 2.282 5.164]]
(b)
A solução do sistema é:
[[ 2.449 0. 0. ]
[ 6.124 4.183 0. ]
[22.454 20.917 6.11 ]]
(c)
A solução do sistema é:
[[ 1.414 0. 0. ]
[-0.707 1.225 0. ]
[ 0. -0.816 1.155]]
(d)
A solução do sistema é:
[[ 2. 0. 0. 0. ]
[ 0.5 1.658 0. 0. ]
[ 0.5 -0.754 1.087 0. ]
[ 0.5 0.452 0.084 1.24 ]]