Sistemas de EDOs
Contents
39. Sistemas de EDOs#
Embora EDOs escalares sejam responsáveis por descrever uma vasta quantidade de fenômenos naturais, muitas aplicações são melhor descritas através de um sistema de EDOs escalares ou de ordem superior. O tratamento numérico de EDOs de alta ordem baseia-se em uma conversão a sistemas de primeira ordem. Vejamos como escrever a forma geral de um sistema de duas EDOS de primeira ordem:
As funções \(f_1(t,z_1,z_2)\) e \(f_2(t,z_1,z_2)\) definem EDOs e as incógnitas são as funções \(y_1(t)\) e \(y_2(t)\). O problema de valor inicial então consiste de resolver o sistema anterior, sujeito às condições iniciais \(y_1(t_0) = y_{1,0}\) e \(y_2(t_0) = y_{2,0}\).
Exemplo: O PVI $\(\begin{cases} y_1'(t) &=& y_1(t) − 2y_2(t) + 4\cos(t) − 2{\rm sen}(t) \\ y_2'(t) &=& 3y_1(t) − 4y_2(t) + 5\cos(t) − 5{\rm sen}(t) \\ y_1(0) &=& 1 \\ y_2(0) &=& 2 \end{cases}\)$
tem por solução as funções \(y_1(t) = \cos(t) + {\rm sen}(t)\) e \(y_2(t) = 2\cos(t)\).
Exemplo (Modelo de Lotka-Volterra): O sistema de EDOs dado por $\(\begin{cases} y_1'(t) &=& A y_1(t)[1 − B y_2(t)] \\ y_2'(t) &=& C y_2(t)[D y_1(t) − 1] \\ y_1(0) &=& y_{1,0} \\ y_2(0) &=& y_{2,0} \end{cases}\)$
com constantes \(A\), \(B\), \(C\), \(D>0\) é conhecido como modelo predador-presa. A variável \(t\) é o tempo, \(y_1(t)\) o número de presas no tempo \(t\) (e.g. coelhos) e \(y_2(t)\) o número de predadores (e.g. raposas). Para apenas um tipo de predador e de presa, este modelo é uma aproximação razoável da realidade.
39.1. Sistema com \(m\) EDOs de primeira ordem#
Um PVI com \(m\) EDOs escalares é dado por
cuja solução procurada são as funções \(y_1(t), y_2(t),\ldots,y_m(t)\). Entretanto, a forma anterior não é computacionalmente adequada para se trabalhar. Assim, simplificamo-na para a forma vetorial
onde
com \({\bf y} = [y_1,y_2,\ldots,y_m]^T\).
Exemplo: O primeiro PVI pode ser reescrito como
com
39.2. Métodos numéricos para sistemas#
Tanto o método de Euler quanto outros métodos numéricos podem ser usados de forma similar para sistemas de EDOs quando aplicados a cada EDO individual. Para isto, lança-se mão da forma matriz/vetor, em que a derivação é essencialmente a mesma feita para o caso individual.
Lembremos que a série de Taylor desenvolvida para o método de Euler é dada por:
para \(m\) EDOs. Desprezando-se os termos de erro, o método de Euler em forma vetorial é escrito como
39.2.1. Implementação computacional#
O seguinte código é uma implementação do método de Euler para resolver sistemas de EDOs. O usuário necessita especificar uma função adicional para determinar as EDOs como componentes de um vetor. Isto é feito pela função
def fsys(t,y):
(...)
return F
from numpy import *
def euler_sys(t0,tf,y0,h,f):
"""
Resolve o PVI de um sistema de EDOs escalares
y’ = f(t,y), t0 <= t <= b, y(t0)=y0 pelo metodo de Euler com tamanho de passo h.
O usuario deve fornecer um vetor f contendo as funcoes a serem avaliadas como
membro direito.
Entrada:
t0 - tempo inicial
tf - tempo final
y0 - condicao inicial
h - passo
f - vetor de funcoes f(t,y) (anonima)
Saída:
t - vetor contendo os valores nodais t[i], i = 1,2,...,n
Y - matriz de dimensoes n x m, com m sendo o numero de EDOs
(a i-esima linha y[i,:] traz as estimativas de todas
as funcoes y_j no tempo t[i])
"""
m = y0.size
n = round((tf - t0)/h + 1)
t = linspace(t0,t0+(n-1)*h,n)
Y = zeros((n,m))
Y[0,:] = y0
for i in range(1,n):
Y[i,:] = Y[i-1,:] + h*f(t[i-1],Y[i-1,:])
return t,Y
Exercício resolvido: Resolva o PVI abaixo pelo método de Euler:
com
Resolver numericamente pelo método de Euler para \(0 < t \le 5\) e \(h = 0.5\).
# define funcao vetorial f(t,y)
def fsys(t,y):
"""
Função definida pelo usuario para montar vetor das m funcoes fm(t,(y1,...,ym))
Em cada componente prescrevemos a funcao da EDO correspondente no sistema
de m EDOs.
Isto e,
F = [f1(t,y1,...,ym),f2(t,y1,...,ym),...,fm(t,y1,...,ym)]^T
Neste exemplo, o sistema possui 2 EDOs, com:
f1(t,y1,y2) = y1 - 2y2 + 4cos(t) - 2sin(t)
f2(t,y1,y2) = 3y1 - 4y2 + 5cos(t) - 5sin(t)
"""
F = array([y[0]-2*y[1]+4*cos(t)-2*sin(t),3*y[0]-4*y[1]+5*cos(t)-5*sin(t)])
return F
from matplotlib.pyplot import plot,legend
# parâmetros
t0,tf = 0,5
h = 0.05
y0 = array([1,2])
# solução numérica do sistema
t,Y = euler_sys(t0,tf,y0,h,fsys)
y1_num = Y[:,0]
y2_num = Y[:,1]
# solução analítica
y1_an = cos(t) + sin(t)
y2_an = 2*cos(t)
# plotagem
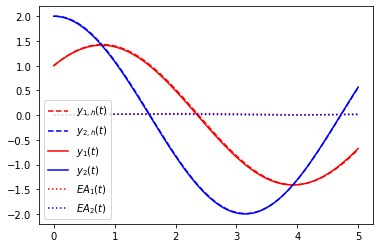
plot(t,y1_num,'r--',label='$y_{1,h}(t)$')
plot(t,y2_num,'b--',label='$y_{2,h}(t)$')
plot(t,y1_an,'r',label='$y_1(t)$')
plot(t,y2_an,'b',label='$y_2(t)$')
# erro absoluto
plot(t,abs(y1_an - y1_num),'r:',label='$EA_1(t)$')
plot(t,abs(y2_an - y2_num),'b:',label='$EA_2(t)$')
legend(loc=3,fontsize=10);
Exercício: Considere o PVI
com
para \(t \in (0,t_f]\) e \( 0 < h < 1\) convenientemente escolhidos. Verifique que a sua solução analítica é dada por \({\bf y} = [\exp(-t), 1]^T\), resolva-o numericamente, plote os gráficos das curvas da solução numérica e do erro relativo para cada uma. Compare os gráficos com aqueles das curvas da solução analítica.
39.3. Problemas#
Problema: considere o modelo de Lotka-Volterra com os parâmetros \(A = 4\), \(B = 1\), \(C = 3\) e \(D = 1\). Usando o método de Euler, resolva-o para \(0 \le t \le 5\). Use passos de \(h = 0.001\), \(0.0005\) e \(0.00025\) e a condição inicial values \(y_1(0) = 3\), \(y_2(0) = 5\). Plote as funções \(y_1\) e \(y_2\) em função de \(t\) e, depois, plote o gráfico de \(y_1\) versus \(y_2\). Comente os resultados.
Problema: Considere o esquema numérico
Tente adaptá-lo para resolver o PVI do Exercício resolvido.

