Método de Newton para sistemas não-lineares
Contents
15. Método de Newton para sistemas não-lineares#
Este método determina, a cada iteração, a solução aproximada do sistema não-linear através de uma linearização das funções-alvo com a matriz Jacobiana associada ao sistema.
15.1. Passos#
Para o método de Newton não-linear, basicamente criamos uma espécie de “caminho” onde somamos um vetor de deslocamento \({\bf s}\) às aproximações sucessivas que dá a direção para onde os vetores devem prosseguir a fim de atingir convergência.
Obs.: este processo iterativo usa critérios de parada naturais em algoritmos iterativos.
Para encontrarmos o vetor solução, devemos resolver a equação matricial linearizada
Em seguida, atualizamos o novo vetor da sequencia como:
Acima, \({\bf J}({\bf x}^{(i)})\) é a matriz Jacobiana formada a partir das derivadas parciais das funções componentes do vetor \({\bf F}\).
No caso de um sistema em que \({\bf F} = [f_1(x_1,x_2) \ \ f_2(x_1,x_2)]^T\), teríamos o sistema abaixo:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import sympy as sy
from scipy.optimize import root
No exemplo a seguir, mostramos como podemos resolver um sistema de equações não-lineares usando o scipy.
Procuramos as soluções para o sistema não-linear
Vamos plotar o gráficos das funções:
x = np.linspace(-2,2,50,endpoint=True)
y = x[:]
X,Y = np.meshgrid(x,y)
# define funções para plotagem
F1 = X**2 + Y**2 - 2
F2 = X**2 - Y**2/9 - 1
# curvas de nível
C = plt.contour(X,Y,F1,levels=[0],colors='k')
C = plt.contour(X,Y,F2,levels=[0],colors='g')
plt.grid(True)
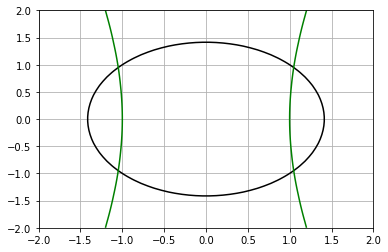
Pela figura, vemos que existem 4 pontos de interseção entre as curvas e, portanto, 4 soluções, as quais formam o conjunto
Agora, vamos usar a função root do scipy para computar essas soluções com base em estimativas iniciais.
# define função para o vetor F(x)
def F(x):
return [ x[0]**2 + x[1]**2 - 2,
x[0]**2 - x[1]**2/9 - 1 ]
x,y = sy.symbols('x,y')
# usa computação simbólica para determinar a matriz Jacobiana
f1 = x**2 + y**2 - 2
f2 = x**2 - y**2/9 - 1
# gradientes
f1x,f1y = sy.diff(f1,x),sy.diff(f1,y)
f2x,f2y = sy.diff(f2,x),sy.diff(f2,y)
# imprime derivadas parciais
print(f1x)
print(f1y)
print(f2x)
print(f2y)
# monta matriz Jacobiana
def jacobian(x):
return np.array([[2*x[0], 2*x[1]], [2*x[0],-2*x[1]/9]])
# resolve o sistema não-linear por algoritmo de Levenberg-Marqardt modificado
inicial = [[2,2],[-2,2],[-2,-2],[2,-2]]
S = []
i = 1
for vetor in inicial:
aux = root(F,vetor,jac=jacobian, method='lm')
S.append(aux.x)
s = 'Solução x({0})* encontrada: {1}'
print(s.format(i,aux.x))
i +=1
2*x
2*y
2*x
-2*y/9
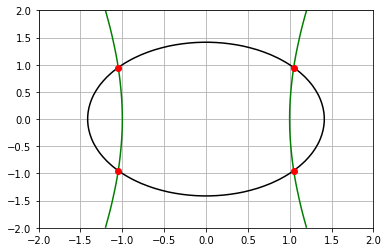
Solução x(1)* encontrada: [1.04880885 0.9486833 ]
Solução x(2)* encontrada: [-1.04880885 0.9486833 ]
Solução x(3)* encontrada: [-1.04880885 -0.9486833 ]
Solução x(4)* encontrada: [ 1.04880885 -0.9486833 ]
Em seguida, vamos plotar as soluções e as curvas
# curvas de nível
C = plt.contour(X,Y,F1,levels=[0],colors='k')
C = plt.contour(X,Y,F2,levels=[0],colors='g')
plt.grid(True)
# imprime interseções
for i in range(len(S)):
plt.plot(S[i][0],S[i][1],'or')
15.1.1. Exercício:#
Resolva os sistemas não-lineares da Lista de Exercícios 4 usando a mesma abordagem acima.
16. Nota: Raízes de sistemas não-lineares#
Uma equação linear tem a forma:
Uma equação não-linear possui “produtos de incógnitas”, e.g.
Um sistema de equações não-lineares é composto de várias equações não-lineares
A solução do sistema é o vetor \( (x_1^{*},x_2^{*},\ldots,x_n^{*}) \) que satisfaz as \( n \) equações simultaneamente.
16.1. Iteração de Ponto Fixo para sistemas não-lineares#
Aplicar o algoritmo iterativo em cada componente:
As formas funcionais mudam porque devemos isolar a variável \( x_i \).
Exemplo: encontrar a raiz do sistema abaixo:
Solução:
Reescrevamos as equações na forma
de onde temos a iteração de ponto fixo dada por
Usando \( (x^0,y^0) = (1.5,3.5) \) como “chute” inicial, computamos
O processo iterativo converge para a solução \( (x^{*},y^{*}) = (2,3) \).
Notas:
A convergência por iteração de PF depende de como as equações \( \tilde{f}_1,\tilde{f}_2,\ldots,\tilde{f}_n \) são formuladas, bem como de um bom “chute” inicial.
A iteração de PF é bastante restritiva nas soluções de sistemas não-lineares.
16.2. Newton-Raphson para sistema não-linear#
Depende de série de Taylor em \( n-\)dimensões.
Para 2 dimensões, por exemplo, o método de Newton-Raphson pode ser escrito como:
A estimativa da raiz corresponde aos valores de \( x \) e \( y \) para os quais \( u_{i+1} = 0 \) e \( v_{i+1} = 0 \). Então,
que é um sistema nas incógnitas \( x_{i+1} \) e \( y_{i+1} \).
Manipulações algébricas permitem solucionar este sistema (e.g. regra de Cramer):
onde
é o determinante da matriz Jacobiana do sistema.
Exemplo: resolver o mesmo sistema do PF
Solução:
Inicialmente, calculemos as derivadas parciais no ponto inicial:
O determinante é \( J = 6.5(32.5) - 1.5(36.75) = 156.125 \).
Calculamos os valores da função no ponto inicial
Calculamos os valores no próximo passo, i.e., \( (x^1,y^1) \).
O processo iterativo converge para a solução \( (x^{*},y^{*}) = (2,3) \).
Ref.: Chapra & Canale, sec. 6.6

