Recorte 4: Dígitos significativos, precisão e acurácia

Sobre dígitos significativos

Dígitos significativos referem-se formalmente à confiabilidade de um valor numérico. Isto é, são aqueles que podem ser usados com “confiança”.

Ao aferirmos uma quantidade por algum instrumento de medição, estaremos sujeitos à escala daquele instrumento e, portanto, limitados quanto ao nosso grau de “certeza”.

Por exemplo, as réguas usuais que compramos em uma papelaria possuem o milímetro como menor unidade de medida. Então, se usarmos esta régua para aferir um comprimento real de 12.36 mm, os dígitos 3 e 6 estarão comprometidos. Por sua vez, podemos apenas dizer que o comprimento está entre 12.0 mm e 13.0 mm. Usando a regra do arredondamento, diríamos, finalmente, que é 12.0 mm.

Um exemplo adicional é o valor dos quilômetros rodados por um automóvel. Digamos que o odômetro marque um valor como o da figura abaixo.

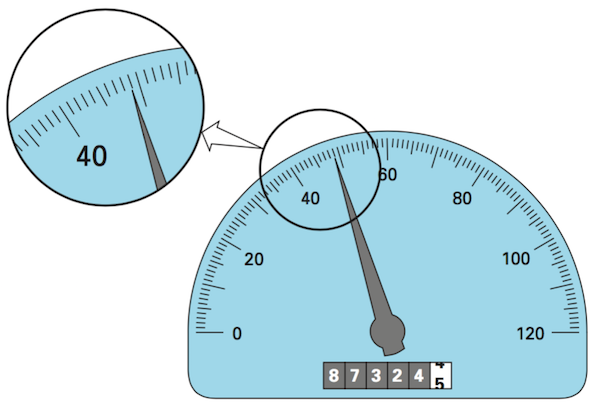
Fig. 1 Dígitos significativos no odômetro de um veículo. Fonte: Chapra e Canale, 2016.

Não poderíamos afirmar que o carro tenha rodado, por suposição, exatos 87.324,45786 km. Podemos apenas dizer que o valor está entre 87.324,4 e 87.324,5.

É comum usar metade da menor divisão da escala do instrumento de medida. Então, no caso do odômetro, poderíamos estimar a medida como 87.324,45, com 87.324,4 formando 6 dígitos certos e 0,05 tendo o dígito 5 como estimado, totalizando um número com 7 dígitos significativos.

Apesar de os exemplos dados serem elucidativos, há outras regras a observar a respeito de dígitos significativos. Consideremos, por exemplo, o número $\( 0.0030400 \)$

• O primeiro 0, à esquerda do ponto flutuante não é significativo. A propósito, como diz o dito popular: um “0 à esquerda é algo sem valor”.

• 00 antes de 3 também não são significativos, assim como não o são aqueles após o ponto flutuante antes de um número diferente de 0.

• O 0 entre 3 e 4 é significativo, assim como todos os 0 entre dois inteiros diferentes de 0 após o ponto flutuante.

• Todos os inteiros diferentes de 0 após o ponto flutuante são significativos.

• 00 após o 4 são significativos, assim como todos aqueles que à direita do ponto flutuante e no final do número.

Precisão e acurácia

Precisão (precision) e acurácia (accuracy) são duas palavras frequentemente usadas como sinônimos, mas, na verdade, elas, possuem significados distintos. Erros associados a cálculos ou medições são caracterizados em relação a esses dois conceitos:

• Acurácia: grau de proximidade com que um valor computado ou medido concorda com o valor verdadeiro.

• Precisão: grau de proximidade com que os valores computados ou medidos concordam um com o outro.

O conceito oposto de acurácia é o viés (bias), ao passo que o de precisão é a incerteza (uncertainty), ou simplesmente imprecisão.

Uma ilustração que facilita a compreensão desses conceitos é o jogo de tiro ao alvo. A marca central caracteriza o valor verdadeiro, desejado. Os pontos ao redor são os resultados das tentativas do jogador. Analogamente, uma técnica numérica pode se comportar. No esquema a seguir, a escala de precisão aumenta de cima para baixo, enquanto que a de acurácia aumenta da esquerda para a direita:

• (a): viciado e impreciso

• (b): acurado e impreciso

• ©: viciado e preciso

• (d): acurado e preciso

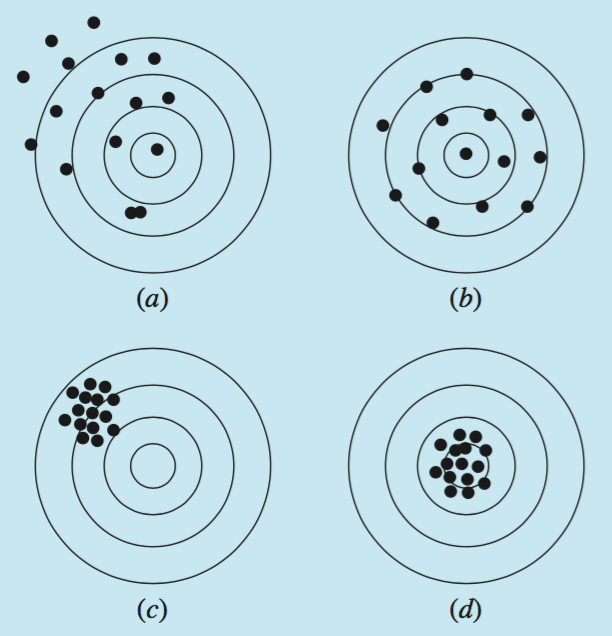
Fig. 2 Precisão vs. acurácia. Fonte: Chapra e Canale, 2016.