Lista de Exercícios 2
Contents
Lista de Exercícios 2#
Solucionário matemático e computacional de exercícios selecionados da Lista de Exercícios 2.
%matplotlib inline
import metodosRaizes as rz
import numpy as np
import sympy as sy
import matplotlib.pyplot as plt
Q12 - L2#
Primeiramente, recorramos à análise gráfica da função.
from numpy import cos, exp
# funcao
p = lambda x: 2*cos(x) - exp(x)
# plotagem
x = np.linspace(-1,1,30)
plt.plot(x,p(x),x,0*p(x));
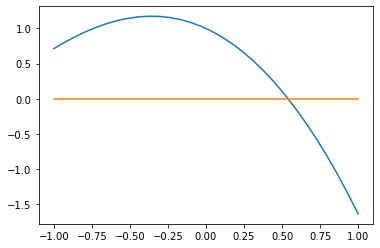
Vemos que a raiz está próxima de \(x= 0.5\). Assim, qualquer valor próximo a este é razoável como aproximação inicial.
Agora, antes de aplicar o método de Newton, vamos calcular a derivada da função simbolicamente.
# derivada simbolica
xsym = sy.Symbol('x')
sy.diff(2*sy.cos(xsym) - sy.exp(xsym),xsym)
Resolvamos com a nossa função programada.
x0 = 0.2
tol = 1e-3
f = '2*cos(x) - exp(x)'
df = '-2*sin(x) - exp(x)'
xr = rz.newton(x0,f,df,tol,10,True)
Estimativa inicial: x0 = 0.2
i x f(x) df(x) ER
0 0.200000 0.738730 -1.618741 -
1 0.656361 -0.343328 -3.148240 6.952896e-01
2 0.547307 -0.020734 -2.769371 1.992555e-01
3 0.539820 -0.000096 -2.743662 1.386900e-02
4 0.539785 -0.000000 -2.743542 6.499799e-05
Solução obtida: x = 0.5397851616
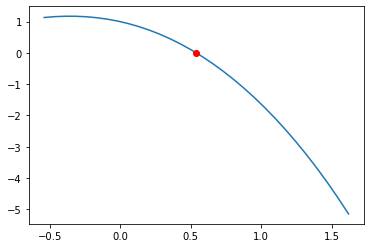
Verificação:
2*cos(xr) - exp(xr)
-2.1118811144305027e-09
Q16 - L2#
p = lambda x: x**5 - 10/9*x**3 + 5/21*x
x = np.linspace(-1,1,50,endpoint=True)
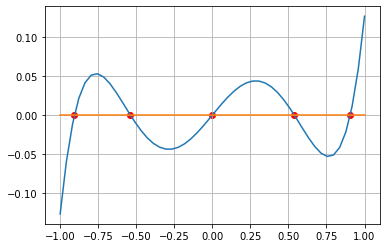
plt.plot(x,p(x),x,0*p(x))
xr = np.roots([1,0,-10/9,0,5/21,0])
print(xr)
plt.scatter(xr,0*xr,c='r');
plt.grid(True);
[-0.90617985 -0.53846931 0.90617985 0.53846931 0. ]
tol = 1e-3
nmax = 100
item b.1)#
# Aproximacao de xi1 pelo MNR
x0 = -0.8
p = 'x**5 - 10/9*x**3 + 5/21*x'
dp = '5*x**4 -10/3*x**2 + 5/21'
plotar = True
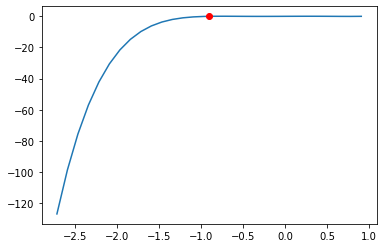
rz.newton(x0,p,dp,tol,nmax,True)
Estimativa inicial: x0 = -0.8
i x f(x) df(x) ER
0 -0.800000 0.050733 0.152762 -
1 -1.132103 -0.517006 4.179132 2.933506e-01
2 -1.008392 -0.143443 2.018543 1.226817e-01
3 -0.937329 -0.031683 1.169040 7.581417e-02
4 -0.910227 -0.003604 0.908555 2.977501e-02
5 -0.906261 -0.000070 0.873137 4.376698e-03
6 -0.906180 -0.000000 0.872424 8.905774e-05
Solução obtida: x = -0.9061798789
-0.9061798789481786
ff = lambda x: x**5 - 10/9*x**3 + 5/21*x
dff = lambda x: 5*x**4 - 30/9*x**2 + 5/21
xx = 0.857
ff(xx),dff(xx)
(-0.03303209894521281, 0.4870085727669044)
item b.2)#
# Aproximacao de xi2 pelo MB
var = 'x'
a,b = -0.75, -0.25
rz.bissecao(p,a,b,tol,100,var)
i=1 a=-0.750000 b=-0.250000 xm=-0.500000 f(a)=0.052874 f(b)=-0.043139 f(xm)=-0.011409 b-a=0.500000
i=2 a=-0.750000 b=-0.500000 xm=-0.625000 f(a)=0.052874 f(b)=-0.011409 f(xm)=0.027090 b-a=0.250000
i=3 a=-0.625000 b=-0.500000 xm=-0.562500 f(a)=0.027090 f(b)=-0.011409 f(xm)=0.007512 b-a=0.125000
i=4 a=-0.562500 b=-0.500000 xm=-0.531250 f(a)=0.007512 f(b)=-0.011409 f(xm)=-0.002211 b-a=0.062500
i=5 a=-0.562500 b=-0.531250 xm=-0.546875 f(a)=0.007512 f(b)=-0.002211 f(xm)=0.002605 b-a=0.031250
i=6 a=-0.546875 b=-0.531250 xm=-0.539062 f(a)=0.002605 f(b)=-0.002211 f(xm)=0.000183 b-a=0.015625
Solução encontrada: -0.5390625
-0.5390625
item b.3)#
# Aproximacao de xi3 pelo MFP
a,b = -0.35, 0.25
rz.falsa_posicao(p,a,b,tol,100,var)
i=1 a=-0.350000 b=0.250000 xm=-0.057823 f(a)=-0.040947 f(b)=0.043139 f(xm)=-0.013553 b-a=0.600000
i=2 a=-0.057823 b=0.250000 xm=0.015767 f(a)=-0.013553 f(b)=0.043139 f(xm)=0.003750 b-a=0.307823
i=3 a=-0.057823 b=0.015767 xm=-0.000181 f(a)=-0.013553 f(b)=0.003750 f(xm)=-0.000043 b-a=0.073590
Solução encontrada: -0.00018060189341005293
-0.00018060189341005293
item b.4)#
# Aproximacao de xi4 pelo MPF
g = '( 0.9*(5/21 + x**5))**1./3.'
#g = eval('lambda x:' + g)
#plt.plot(x,g(x))
rz.ponto_fixo(0.4,p,g,tol,nmax,True)
i x f(x) ER
0 0.400000 0.034367 2.500000e+00
1 0.074501 0.017281 4.369086e+00
2 0.071429 0.016604 4.299795e-02
3 0.071429 0.016604 1.829703e-06
0.07142912925875246
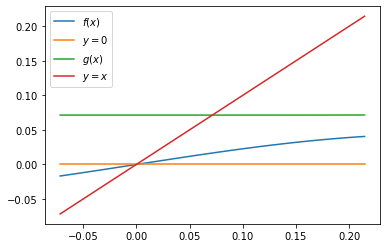
item b.5)#
# Aproximacao de xi5 pelo MS
p = 'x**5 - 10/9*x**3 + 5/21*x'
x0,x1=0.8,1.
rz.secante(x0,x1,p,tol,nmax,True)
Estimativas iniciais: xa = 0.8; xb = 1.0
i x f(x) ER
1 0.857094 -0.032986 1.667334e-01
2 0.886562 -0.015467 3.323813e-02
3 0.912577 0.005764 2.850796e-02
4 0.905514 -0.000579 7.799970e-03
5 0.906159 -0.000018 7.112008e-04
Solução obtida: x = 0.9061586909
0.9061586908755153
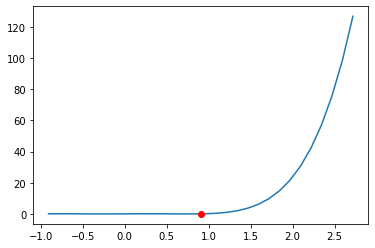
Exemplos#
# exemplo bissecao
rz.bissecao('x**3-9*x+3',0,1,1e-3,100,var)
i=1 a=0.000000 b=1.000000 xm=0.500000 f(a)=3.000000 f(b)=-5.000000 f(xm)=-1.375000 b-a=1.000000
i=2 a=0.000000 b=0.500000 xm=0.250000 f(a)=3.000000 f(b)=-1.375000 f(xm)=0.765625 b-a=0.500000
i=3 a=0.250000 b=0.500000 xm=0.375000 f(a)=0.765625 f(b)=-1.375000 f(xm)=-0.322266 b-a=0.250000
i=4 a=0.250000 b=0.375000 xm=0.312500 f(a)=0.765625 f(b)=-0.322266 f(xm)=0.218018 b-a=0.125000
i=5 a=0.312500 b=0.375000 xm=0.343750 f(a)=0.218018 f(b)=-0.322266 f(xm)=-0.053131 b-a=0.062500
i=6 a=0.312500 b=0.343750 xm=0.328125 f(a)=0.218018 f(b)=-0.053131 f(xm)=0.082203 b-a=0.031250
i=7 a=0.328125 b=0.343750 xm=0.335938 f(a)=0.082203 f(b)=-0.053131 f(xm)=0.014474 b-a=0.015625
i=8 a=0.335938 b=0.343750 xm=0.339844 f(a)=0.014474 f(b)=-0.053131 f(xm)=-0.019344 b-a=0.007812
i=9 a=0.335938 b=0.339844 xm=0.337891 f(a)=0.014474 f(b)=-0.019344 f(xm)=-0.002439 b-a=0.003906
i=10 a=0.335938 b=0.337891 xm=0.336914 f(a)=0.014474 f(b)=-0.002439 f(xm)=0.006017 b-a=0.001953
i=11 a=0.336914 b=0.337891 xm=0.337402 f(a)=0.006017 f(b)=-0.002439 f(xm)=0.001789 b-a=0.000977
Solução encontrada: 0.33740234375
0.33740234375
rz.falsa_posicao('x**3-9*x+3',0,1,1e-3,100,var)
i=1 a=0.000000 b=1.000000 xm=0.375000 f(a)=3.000000 f(b)=-5.000000 f(xm)=-0.322266 b-a=1.000000
i=2 a=0.000000 b=0.375000 xm=0.338624 f(a)=3.000000 f(b)=-0.322266 f(xm)=-0.008790 b-a=0.375000
i=3 a=0.000000 b=0.338624 xm=0.337635 f(a)=3.000000 f(b)=-0.008790 f(xm)=-0.000226 b-a=0.338624
Solução encontrada: 0.33763504551140067
0.33763504551140067
Problemas aplicados#
A temperatura \(T\) (em graus Kelvin) de um semicondutor pode ser calculada como uma função da resistência \(R\) (em ohms) pela equação de Steinhart-Hart:
para constantes \(A\), \(B\) e \(C\) dependentes do material. Supondo que \(A = 1.4056 \times 10^{-3}\), \(B = 240.7620 \times 10^{-6} K^{-1}\) e \(C = 7.48 \times 10^{-7}\), determine a resistência do semicondutor para uma temperatura de 135 graus Celsius.
Sugestão: use o método da bisseção e tolerância de \(10^{-6}\).
Solução computacional#
from scipy.optimize import bisect
# constantes
A = 1.4056e-3
B = 240.7620e-6
C = 7.48e-7
Tc = 135.0 # temperatura em Celsius
Tk = Tc + 273.15 # temperatura em Kelvin
# f(R) = 0
f = lambda R: 1/(A + B*np.log(R) + C*np.log(R)**3) - Tk
# localização
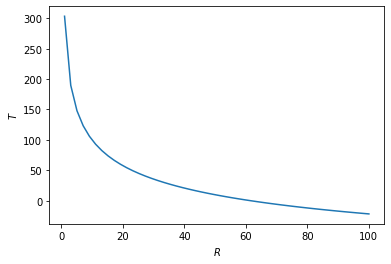
R = np.linspace(1,100,50,True)
plt.plot(R,f(R))
plt.xlabel('$R$')
plt.ylabel('$T$')
# refinamento a=1; b=100
x = bisect(f,1,100,xtol=1e-6)
print("Para {0:.2f} graus Celsius, a resistência é de {1:.2f} ohms".format(Tc,x))
Para 135.00 graus Celsius, a resistência é de 61.61 ohms
Problema aplicado (revisar!)#
Quando se calcula o pagamento de uma hipoteca, a relação entre o montante do empréstimo \(E\), o pagamento mensal \(P\), a duração do empréstimo em anos \(a\), e a taxa de juros anual \(t\) é dada pela equação:
Determine a taxa \(t\) de um empréstimo de R$ 170.000 00 por 20 anos se o pagamento mensal for de R$ 1.250,00.
Sugestão: usar método de Newton como função programada pelo estudante ou função residente.
Solução computacional#
Resolver o problema \(f(t) = 0\) com método de Newton.
from scipy.optimize import newton
from sympy.utilities.lambdify import lambdastr
E = 170000 # montante do empréstimo
P = 1250 # pagamento mensal
a = 20 # duração do empréstimo em anos
# define função para computar
# t: taxa de juros (incógnita)
def taxa_anuidade(E,P,a):
Esym,t,asym,Psym = sy.symbols('Esym t asym Psym')
fsym = Esym*t/( 12*(1 - 1/(1 + t/12)**(12*asym) ) ) - Psym
dfsym = sy.diff(fsym,t)
f = fsym.subs({'Esym':E,'asym':a,'Psym':P})
df = dfsym.subs({'Esym':E,'asym':a,'Psym':P})
ft = eval(lambdastr(t,f))
dft = eval(lambdastr(t,df))
# Aplicação do método de Newton
# parâmetros
t0 = 1.0 # estimativa inicial
tole=1e-3 # tolerância de erro
nmax=50 # número máximo de iterações
# método de Newton
t = newton(ft,t0,dft,tol=tole,maxiter=nmax)
msg = "A taxa do empréstimo é de {0:.2f}% a.a.".format(t*100)
return (t,msg)
# invoca função
taxa_anuidade(E,P,a)
# não sei se a equação do livro está correta: negativo até 12
# aa = np.arange(1,50)
# tt = []
# for i in aa:
# t=taxa_anuidade(E,P,i)
# print(t[1])
# tt.append(t[0])
# tt = np.asarray(tt)
# plt.plot(aa,tt)
(0.0632479251521274, 'A taxa do empréstimo é de 6.32% a.a.')

