33. Campos de direção

Campos de direção são úteis para entender o comportamento das soluções de uma EDO. O gráfico de uma solução da equação \(y' = f(t,y)\) é aquele que, para todo ponto \((t,y)\) do plano, conhecemos a inclinação da curva \(y(t)\), solução da EDO. Campos de direção podem ser plotados em Python através das funções meshgrid, do pacote numpy, e quiver, do pacote matplotlib.

Exemplo Consideremos a EDO \(y'= y\). A inclinação é dada por \(f(t,y) = y\) e é independente de \(t\). Vamos gerar o diagrama do campo de direções para esta EDO pelo código a seguir.

import numpy as np 
import matplotlib.pyplot as plt 

# parametros
t0, tb = 0, 1
y0, yb = -6, 6
nt, ny = 10, 20

# dominio (t,y)
t = np.linspace(t0,tb,nt)
y = np.linspace(y0,yb,ny)
[T,Y] = np.meshgrid(t,y)

# EDO 
dt = np.ones(T.shape)
dy = Y

# campo
f = plt.figure(figsize=(6,5))

plt.quiver(T,Y,dt,dy,color='red')

# solucoes particulares 
y_part = lambda c: c*np.exp(t)

for c in [0.6,0.2,-0.3,-0.7]:
    aux = y_part(c)
    plt.plot(t,y_part(aux))    

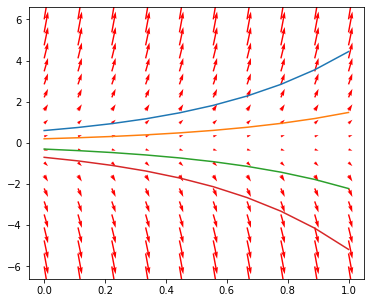
A solução geral desta EDO é \(y(t) = ce^{t}\). Na figura, destacamos quatro soluções particulares, para valores \(c \in \{0.6,0.2,-0.3,-0.7\}\).

Exemplo: Vamos gerar o diagrama do campo de direções para a EDO \(y' = 1/(1-t^2)\).

import numpy as np 
import matplotlib.pyplot as plt 

# parametros
t0, tb = -5, 5
y0, yb = -6, 6
nt, ny = 10, 20

# dominio (t,y)
t = np.linspace(t0,tb,nt)
y = np.linspace(y0,yb,ny)
[T,Y] = np.meshgrid(t,y)

# EDO 
dt = np.ones(T.shape)
dy = 1./(1-T**2)

# campo
f = plt.figure(figsize=(6,5))
plt.quiver(T,Y,dt,dy,color='b');

33.1. Problemas

1. Use o Python para plotar os campos de direção para a família de soluções de cada PVI do Problema 1 da Aula 1.

2. Em cada caso, plote as soluções particulares que você encontrou com a substituição de \(c\).