Code Session 3: Raízes de Polinômios#

import numpy as np, matplotlib.pyplot as plt

Determinação de raízes de polinômios#

roots#

A função roots computa as raízes de uma função dentro de um intervalo dado usando o método de Hörner. O único argumento de entrada desta função é

  1. o array p com os coeficientes dos termos do polinômio.

\[P(x) = p_n x^n + p_{n-1} x^{n-1} + \ldots + p_1x + p_0\]

O argumento de saída é:

  • x: array com as raízes de \(P(x)\).

Problema 1#

Determine as raízes de \(P(x) = 3x^3 +7x^2 - 36x + 20\).

Resolução#

Para tornar claro, em primeiro lugar, vamos inserir os coeficientes de \(P(x)\) em um array chamado p.

p = np.array([9,8,7,5,3,2,-1,-3.2,-4/5,])

Em seguida, fazemos:

x = np.roots(p)

Podemos imprimir as raízes da seguinte forma:

for (i, v) in enumerate(x):
    print(f'Raiz {i}: {v}')

Raiz 0: (0.42664911463435407+0.8028394391214156j)
Raiz 1: (0.42664911463435407-0.8028394391214156j)
Raiz 2: (0.6712830069677369+0j)
Raiz 3: (-0.3125768604422946+0.8705110785366039j)
Raiz 4: (-0.3125768604422946-0.8705110785366039j)
Raiz 5: (-0.7511803685416447+0.3009598192701515j)
Raiz 6: (-0.7511803685416447-0.3009598192701515j)
Raiz 7: (-0.2859556671574551+0j)

polyval#

Podemos usar a função polyval do numpy para avaliar \(P(x)\) em \(x = x_0\). Verifiquemos, analiticamente, se as raízes anteriores satisfazem realmente o polinômio dado.

for i in x: 
    v = np.polyval(p,i)
    print(f'P(x) = {v}')

P(x) = (2.1094237467877974e-14+1.942890293094024e-15j)
P(x) = (2.1094237467877974e-14-1.942890293094024e-15j)
P(x) = (-1.3322676295501878e-14+0j)
P(x) = (-6.217248937900877e-15-8.326672684688674e-16j)
P(x) = (-6.217248937900877e-15+8.326672684688674e-16j)
P(x) = (-1.1102230246251565e-16+8.326672684688674e-16j)
P(x) = (-1.1102230246251565e-16-8.326672684688674e-16j)
P(x) = (-5.551115123125783e-16+0j)

Note que as duas últimas raízes são “muito próximas” de zero, mas não exatamente zero.

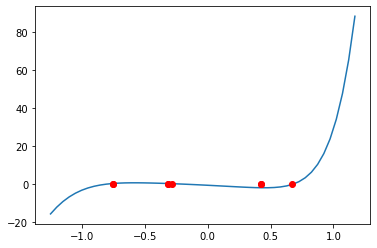
Podemos também fazer uma verificação geométrica plotando o polinômio e suas raízes.

xx = np.linspace(np.min(x)-0.5,np.max(x)+0.5)
plt.plot(xx,np.polyval(p,xx));
for i in x:
    plt.plot(i,np.polyval(p,i),'or')

/Users/gustavo/opt/anaconda3/lib/python3.9/site-packages/matplotlib/cbook/__init__.py:1335: ComplexWarning: Casting complex values to real discards the imaginary part
  return np.asarray(x, float)
../_images/codeSession-3-polyval_17_1.png

Problema 2#

Determine as raízes de \(P(x) = x^4 - 3x^2 + 3x\).

Resolução#

Resolvendo diretamente com roots e usando polyval para verificação, temos:

# coeficientes e raízes
p = np.array([1,0,-3,3,0])
x = np.roots(p)

# imprimindo as raizes
for i, v in enumerate(x):
    print(f'Raiz {i}: {v}')

Raiz 0: (-2.1038034027355357+0j)
Raiz 1: (1.051901701367768+0.5652358516771712j)
Raiz 2: (1.051901701367768-0.5652358516771712j)
Raiz 3: 0j

Note que, neste caso, as raízes são complexas.

Problema 3#

Determine as raízes de \(P(x) = x^5 - 30x^4 + 361x^3 - 2178x^2 + 6588x - 7992\).

Resolução#

# coeficientes e raízes
p = np.array([1,-30,361,-2178,6588,-7992])
x = np.roots(p)

# imprimindo as raizes
for i, v in enumerate(x):
    print(f'Raiz {i}: {v}')

Raiz 0: (6.000000000009944+0.9999999999996999j)
Raiz 1: (6.000000000009944-0.9999999999996999j)
Raiz 2: (6.00026575921113+0j)
Raiz 3: (5.999867120384507+0.0002301556526862668j)
Raiz 4: (5.999867120384507-0.0002301556526862668j)