Code Session 6: Interpolação

interp1d

A classe interp1d do submódulo scipy.interpolate pode ser usada como uma estrutura genérica para o cálculo de interpolação unidimensional do tipo \(y_k = f(x_k)\).

Para usar interp1d, precisamos de, no mínimo, uma tabela de dados fornecida por dois parâmetros:

1. x: array de valores independentes

2. y: array de valores dependentes

Um dos argumentos opcionais relevantes de interp1d é:

• kind: tipo de dado str ou int que especifica o tipo de interpolação.

O valor padrão de kind é 'linear', o qual equivale à configuração de uma interpolação linear. Outras opções relevantes, bem como o que elas realizam estão dispostas na tabela a seguir:

opção	interpolação
'nearest'	vizinho mais próximo
'zero'	interpolação por spline de ordem 0
'slinear'	interpolação por spline de ordem 1
'quadratic'	interpolação por spline de ordem 2
'cubic'	interpolação por spline de ordem 3

Se um valor inteiro for passado para 'kind', ele indicará a ordem da spline interpolatória. Por exemplo, 'kind' = 4 indica uma interpolação por spline de ordem 4.

Em Python, a classe interp1d é chamada da seguinte forma:

from scipy.interpolate import interp1d

Podemos, agora, resolver alguns problemas de interpolação unidimensional por meio desta classe.

Em primeiro lugar, vamos importar alguns módulos necessários para nossos cálculos.

import numpy as np
import matplotlib.pyplot as plt 
from scipy.interpolate import interp1d

Problema 1

Valores de entalpia por unidade de massa, \(h\), de um plasma de Argônio em equilíbrio versus temperatura estão tabelados no arquivo file-cs6-entalpia.csv. Usando esses dados:

• Escreva um programa para interpolar valores de \(h\) para temperaturas no intervalo \(5000 - 30000 \, ^{\circ}K\), com incrementos de \(500 \, ^{\circ}K\).

• Plote o gráfico de dispersão marcando com asteriscos os valores de entalpia tabelados. Em seguida, plote gráficos de linha para as seguintes interpolações: 'nearest', 'zero', 'slinear' e 'quadratic'.

• Compare os valores interpolados de \(h\) para cada um dos métodos de interpolação 'zero', 'slinear' e 'quadratic' do item anterior para \(T= 15150 \, ^{\circ}K\).

Observação: note que a temperatura da tabela deve ser multiplicada por 1000.

Resolução

Em primeiro lugar, vamos ler a tabela de dados, atribuir os valores tabelados em arrays e corrigir os valores de temperatura pelo fator 1000.

# atribuindo colunas da matriz de dados em h e T
h, T = np.loadtxt('../file-cs6-entalpia.csv', delimiter=',', skiprows=1, unpack=True)

# temperatura em milhares de Kelvin
T = 1e3*T 

T

array([ 5000.,  7500., 10000., 12500., 15000., 17500., 20000., 22500.,
       25000., 27500., 30000.])

Criamos um array para o intervalo de temperaturas desejado para interpolação usando arange. Notemos que esta função exige um deslocamento do valor do incremento no último elemento do array, isto é, 30000 + 500 = 30500.

# array de temperaturas com incremento de 500 K
t = np.arange(5000.0,30500.0,500)

Em seguida, usamos os valores tabelados para posterior aplicação de interp1d sobre t como uma função e imprimimos os valores interpolados de entalpia:

# montagem da interpolação
f = interp1d(T,h)

# valores interpolados
hi = f(t) 

array([  3.3 ,   4.14,   4.98,   5.82,   6.66,   7.5 ,  14.36,  21.22,
        28.08,  34.94,  41.8 ,  43.8 ,  45.8 ,  47.8 ,  49.8 ,  51.8 ,
        53.64,  55.48,  57.32,  59.16,  61.  ,  69.02,  77.04,  85.06,
        93.08, 101.1 , 107.46, 113.82, 120.18, 126.54, 132.9 , 135.42,
       137.94, 140.46, 142.98, 145.5 , 150.68, 155.86, 161.04, 166.22,
       171.4 , 182.28, 193.16, 204.04, 214.92, 225.8 , 232.82, 239.84,
       246.86, 253.88, 260.9 ])

Vamos determinar os valores interpolados para cada método de interpolação e plotá-los juntamente com o gráfico de dispersão dos valores tabelados.

# métodos de interpolação
m = ['nearest','zero','slinear', 'quadratic','cubic',5,7,9]

# objetos de interpolação para cada método 
F = [interp1d(T,h,kind=k) for k in m]
print(F)

# valores interpolados
him = [f(t) for f in F]

# plotagem dos valores tabelados
plt.plot(T,h,'*',label='tabelado');

# plotagem dos métodos
for i in range(len(m)):
    plt.plot(t,him[i],label=m[i])

# legenda
plt.legend();    

[<scipy.interpolate._interpolate.interp1d object at 0x7ff331e54130>, <scipy.interpolate._interpolate.interp1d object at 0x7ff331e541d0>, <scipy.interpolate._interpolate.interp1d object at 0x7ff331e54220>, <scipy.interpolate._interpolate.interp1d object at 0x7ff33199e810>, <scipy.interpolate._interpolate.interp1d object at 0x7ff331e51450>, <scipy.interpolate._interpolate.interp1d object at 0x7ff331dd06d0>, <scipy.interpolate._interpolate.interp1d object at 0x7ff331dbc130>, <scipy.interpolate._interpolate.interp1d object at 0x7ff331a6ff90>]

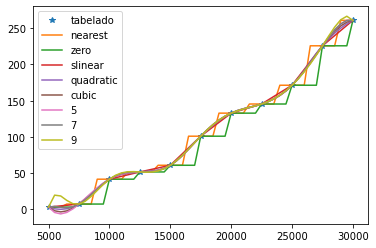
Até aqui, já cumprimos os dois primeiros requisitos do problema. Para o terceiro, usaremos as informações pré-computadas na lista F para estimar os valores de entalpia quando \(T = 15150 \, ^{\circ} K\). Teremos os seguintes três valores:

# calcula h(15150) para os métodos 'zero', 'slinear' e 'quadratic'
h_15150 = [f(15150) for f in F[1:]]

h_15150

[array(61.),
 array(63.406),
 array(62.60353522),
 array(62.64452478),
 array(62.63805504),
 array(62.68643145),
 array(62.73084339)]

Isto é, os valores de entalpia em \(T = 15150 \, ^{\circ} K\) podem ser organizdos na tabela a seguir:

método	valor
'zero'	61.0 MJ/kg
'slinear'	63.406 MJ/kg
'quadratic'	62.604 MJ/kg

Levando em conta que quanto mais alta é a ordem de interpolação, melhor é a interpolação, podemos inferir que desses três valores, \(62.604 \, MJ/kg\) é o mais confiável para usar.

Problema 2

O arquivo file-cs6-salinidade.csv tabela valores de salinidade da água (em ppt) em função da profundidade oceânica (em metros). Use interpolação por spline cúbica para gerar uma tabela de salinidades para profundidades de 0 a 3000 m com espaçamento de 10 m e estime os valores nas profundidades de 250 m, 750 m e 1800 m.

Problema 3

A tabela a seguir apresenta a potência de um motor a Diesel (em hp) em diferentes rotações (em rpm). Gere uma tabela de valores interpolados com espaçamento de 10 rpm e destaque as potências em 2300 rpm e 3650 rpm.

velocidade (rpm)	potência (hp)
1200	65
1500	130
2000	185
2500	225
3000	255
3250	266
3500	275
3750	272
4000	260
4400	230