23. Integração Numérica: Quadratura Gaussiana#

Uma característica das fórmulas de Newton-Cotes é estimar a integral com base em valores da função tomados em nós igualmente espaçados. Consequentemente, a posição desses nós é predeterminada, isto é, fixada.

Agora, suponhamos que a restrição de ter nós fixados seja removida e que pudéssemos escolher arbitrariamente as posições por eles ocupadas. Com uma escolha adequada, será que conseguiríamos reduzir o erro de integração?

De fato, o método da Quadratura Gaussiana permite-nos estabelecer um conjunto mínimo de nós e pesos que realizam uma espécie de “balanceamento” do erro (subestimação vs. superestimação) e determinam aproximações numéricas de integrais com alta ordem.

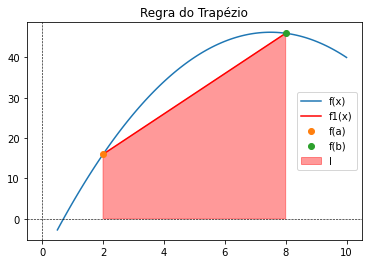
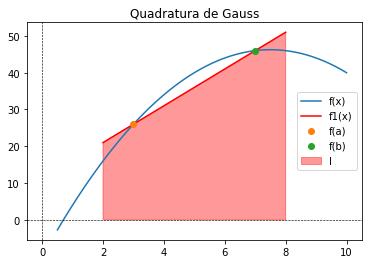
As figuras abaixo mostram, por exemplo, como a integral de uma função \(f(x)\) é melhor calculada através da colocação de pontos em posições “especiais”. A regra do trapézio é posta em contraste com uma outra regra, que aprenderemos, cujo par de pontos, embora defina também um trapézio, ajuda a estimar melhor a integral de \(f(x)\) do que o observado no primeiro caso.

Em particular, daremos enfoque à chamada Quadratura de Gauss-Legendre.

import matplotlib.pyplot as plt
import numpy.polynomial.legendre as leg
import numpy as np

def f(x):
    return -x**2 + 15*x - 10

x = np.linspace(0.5,10,100)
y = f(x)

# Representação geométrica da regra do trapézio

plt.figure()
plt.plot(x,y, label = 'f(x)')
plt.plot([2,8], [f(2),f(8)], 'r', label = 'f1(x)')
plt.plot(2,f(2), 'o', label = 'f(a)')
plt.plot(8,f(8), 'o', label = 'f(b)')
plt.fill([2, 2, 8, 8],[0, f(2), f(8), 0],color='r',alpha=0.4, label = 'I')
plt.title('Regra do Trapézio')
plt.legend()
plt.axvline(x=0,color='k',linewidth=0.6,linestyle='--')
plt.axhline(y=0,color='k',linewidth=0.6,linestyle='--')

# Representação geométrica da quadratura de Gauss

def f1(x):
    return 5.0*x + 11.0

plt.figure()
plt.plot(x,y, label = 'f(x)')
plt.plot([2,8], [f1(2),f1(8)], 'r', label = 'f1(x)')
plt.plot(3,f(3), 'o', label = 'f(a)')
plt.plot(7,f(7), 'o', label = 'f(b)')
plt.fill([2, 2, 8, 8],[0, f1(2), f1(8), 0],color='r',alpha=0.4, label = 'I')
plt.title('Quadratura de Gauss')
plt.legend()
plt.axvline(x=0,color='k',linewidth=0.6,linestyle='--')
plt.axhline(y=0,color='k',linewidth=0.6,linestyle='--');
_images/aula-19-quadratura-gaussiana_2_0.png _images/aula-19-quadratura-gaussiana_2_1.png

23.1. Dedução da Fórmula de Gauss-Legendre para Dois Pontos#

O objetivo da quadratura de Gauss-Legendre é determinar os coeficientes de uma equação da forma

\[ I \cong c_0 f(x_0) + c_1 f(x_1) \qquad (1) \]

em que os \(c\)’s são coeficientes desconhecidos. Entretanto, em contraste com a regra do trapézio que usa extremidades fixas \(a\) e \(b\), os argumentos da função \(x_0\) e \(x_1\) não são fixados nas extremidades, mas são incógnitas. Assim, agora temos um total de quatro incógnitas que devem ser calculadas e necessitamos de quatro condições para determiná-las exatamente.

Podemos obter duas dessas condições, supondo que a Equação (1) calcula a integral de uma função constante e de uma função linear exatamente. Então, para chegar a duas outras condições, simplesmente estendemos esse raciocínio supondo que ele também calculará a integral de uma função parabólica (\(y = x^2\)) e de uma cúbica (\(y = x^3\)) exatamente. Fazendo isso, determinamos todas as quatro incógnitas e, de quebra, deduzimos uma fórmula de integração linear de dois pontos que é exata para funções cúbicas. As quatro equações a serem resolvidas são:

\[\begin{split} c_0 f(x_0) + c_1 f(x_1) = \int _{-1}^{1} 1 dx = 2 \qquad (2) \\ c_0 f(x_0) + c_1 f(x_1) = \int _{-1}^{1} x dx = 0 \qquad (3) \\ c_0 f(x_0) + c_1 f(x_1) = \int _{-1}^{1} x^2 dx = \dfrac{2}{3} \qquad (4) \\ c_0 f(x_0) + c_1 f(x_1) = \int _{-1}^{1} x^3 dx = 0 \qquad (5) \end{split}\]

As Equações (2) até (5) podem ser resolvidas simultaneamente por

\[\begin{split} c_0 = c_1 = 1 \\ x_0 = -\dfrac{1}{\sqrt{3}} \\ x_1 = \dfrac{1}{\sqrt{3}} \end{split}\]

o que pode ser substituído na Equação (1) para fornecer a fórmula de Gauss-Legendre de dois pontos

\[ I \cong f \left( \dfrac{-1}{\sqrt{3}} \right) + f \left( \dfrac{1}{\sqrt{3}} \right) \qquad (6) \]

Logo, chegamos ao interessante resultado que uma simples adição de valores da função em \(x = 1/\sqrt{3}\) e \(−1/\sqrt{3}\) fornece uma estimativa da integral que tem acurácia de terceira ordem.

Observe que os extremos de integração nas Equações (2) até (5) são de \(−1\) a \(1\). Isso foi feito para simplificar a matemática e tornar a formulação tão geral quanto possível. Uma simples mudança de variável pode ser usada para transformar outros extremos de integração para essa fórmula, o que se faz supondo que uma nova variável \(x_d\) está relacionada à variável original \(x\) de uma forma linear como em

\[ x = a_0 + a_1 x_d \qquad (7) \]

Se o extremo inferior, \(x = a\), corresponder a \(x_d = −1\), esses valores podem ser substituídos na Equação (7) para fornecer

\[ a = a_0 + a_1 (- 1) \qquad (8) \]

Analogamente, o extremo superior, \(x = b\), corresponde a \(x_d = 1\), e fornece

\[ b = a_0 + a_1 (1) \qquad (9) \]

As Equações (8) e (9) podem ser resolvidas simultaneamente por

\[ a_0 = \dfrac{b + a}{2} \]

e

\[ a_1 = \dfrac{b - a}{2} \]

o que pode ser substituído na Equação (7) para fornecer

\[ x = \dfrac{(b + a) + (b - a) x_d}{2} \qquad (10) \]

Essa equação pode ser derivada para dar

\[ dx = \dfrac{b - a}{2} dx_d \qquad (11) \]

Os valores de \(x\) e \(dx\), nas Equações (10) e (11), respectivamente, podem ser substituídos na equação a ser integrada. Essas substituições transformam efetivamente o intervalo de integração sem mudar o valor da integral.

23.2. Fórmulas com Mais Pontos#

Além da fórmula de dois pontos descrita acima, versões com mais pontos podem ser desenvolvidas na forma geral

\[ I \cong c_0 f(x_0) + c_1 f(x_1) + \dots + c_{n−1} f(x_{n−1}) \qquad (12) \]

em que \(n\) é o número de pontos. Os valores para os \(c\)’s e os \(x\)’s para até (e incluindo) a fórmula de quatro pontos estão resumidos na tabela abaixo.

Pontos

Fatores de Peso

Argumentos da Função

3

\(c_0\) = 0.5555556

\(x_0\) = - 0.774596669

\(c_1\) = 0.8888889

\(x_1\) = 0.0

\(c_2\) = 0.5555556

\(x_2\) = 0.774596669

4

\(c_0\) = 0.3478548

\(x_0\) = - 0.861136312

\(c_1\) = 0.6521452

\(x_1\) = - 0.339981044

\(c_2\) = 0.6521452

\(x_2\) = 0.339981044

\(c_3\) = 0.3478548

\(x_3\) = 0.861136312

23.3. Implementação#

Vamos implementar abaixo o código para gerar a tabela de pontos (nós) e pesos para integração numérica consoante as fórmulas de quadratura de Gauss-Legendre.

# número de pontos de quadratura
n = 20

# pontos e pesos
(pontos,pesos) = leg.leggauss(n)        

def F(t):
    return 5.1*np.exp(5.1*t + 1.1)

def QG2(F):
    (pontos,pesos) = leg.leggauss(2)  
    print(pontos,pesos)
    return pesos[0]*F(pontos[0]) + pesos[1]*F(pontos[1])

def QG3(F):
    (pontos,pesos) = leg.leggauss(3)  
    print(pontos,pesos)
    return pesos[0]*F(pontos[0]) + pesos[1]*F(pontos[1]) + pesos[2]*F(pontos[2])

def QG4(F):
    (pontos,pesos) = leg.leggauss(4)  
    print(pontos,pesos)
    return pesos[0]*F(pontos[0]) + pesos[1]*F(pontos[1]) \
+ pesos[2]*F(pontos[2]) + pesos[3]*F(pontos[3])


def QG(F,n):
    (pontos,pesos) = leg.leggauss(n)  
    
    s = 0
    for i in range(n):
        s += pesos[i]*F(pontos[i])

    return s

for i in range(1,20):
    print(f'QG{i} = {QG(F,i)}')

QG1 = 30.642493444253617
QG2 = 291.9238277183161
QG3 = 456.0422383934014
QG4 = 488.96142750746253
QG5 = 492.48121331764094
QG6 = 492.71920635748165
QG7 = 492.7303338909227
QG8 = 492.73071525454685
QG9 = 492.73072524440545
QG10 = 492.7307254508673
QG11 = 492.7307254543184
QG12 = 492.73072545436776
QG13 = 492.73072545436753
QG14 = 492.73072545436855
QG15 = 492.7307254543701
QG16 = 492.73072545436673
QG17 = 492.7307254543697
QG18 = 492.7307254543684
QG19 = 492.73072545437

print(pontos)

[-0.9931286  -0.96397193 -0.91223443 -0.83911697 -0.74633191 -0.63605368
 -0.510867   -0.37370609 -0.22778585 -0.07652652  0.07652652  0.22778585
  0.37370609  0.510867    0.63605368  0.74633191  0.83911697  0.91223443
  0.96397193  0.9931286 ]

e os pesos correspondentes são:

print(pesos)

[0.01761401 0.04060143 0.06267205 0.08327674 0.10193012 0.11819453
 0.13168864 0.14209611 0.14917299 0.15275339 0.15275339 0.14917299
 0.14209611 0.13168864 0.11819453 0.10193012 0.08327674 0.06267205
 0.04060143 0.01761401]

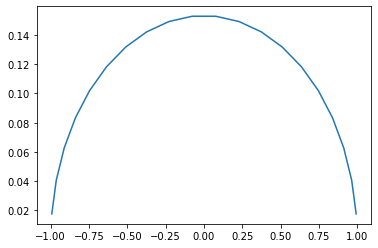
plt.plot(pontos,pesos)
plt.autoscale;
_images/aula-19-quadratura-gaussiana_11_0.png

23.3.1. Tabela de pesos/pontos - Quadratura de Gauss-Legendre#

Para gerarmos uma tabela de pontos e pesos, basta fazer:

# número máximo de pontos
N = 16

for i in range(1,N+1):
    (pontos,pesos) = leg.leggauss(i)       
    print('REGRA DE {0} PONTO(S):\n-> Pontos:'.format(i))
    print(pontos)
    print('-> Pesos:')
    print(pesos)
    print('\n')

REGRA DE 1 PONTO(S):
-> Pontos:
[0.]
-> Pesos:
[2.]


REGRA DE 2 PONTO(S):
-> Pontos:
[-0.57735027  0.57735027]
-> Pesos:
[1. 1.]


REGRA DE 3 PONTO(S):
-> Pontos:
[-0.77459667  0.          0.77459667]
-> Pesos:
[0.55555556 0.88888889 0.55555556]


REGRA DE 4 PONTO(S):
-> Pontos:
[-0.86113631 -0.33998104  0.33998104  0.86113631]
-> Pesos:
[0.34785485 0.65214515 0.65214515 0.34785485]


REGRA DE 5 PONTO(S):
-> Pontos:
[-0.90617985 -0.53846931  0.          0.53846931  0.90617985]
-> Pesos:
[0.23692689 0.47862867 0.56888889 0.47862867 0.23692689]


REGRA DE 6 PONTO(S):
-> Pontos:
[-0.93246951 -0.66120939 -0.23861919  0.23861919  0.66120939  0.93246951]
-> Pesos:
[0.17132449 0.36076157 0.46791393 0.46791393 0.36076157 0.17132449]


REGRA DE 7 PONTO(S):
-> Pontos:
[-0.94910791 -0.74153119 -0.40584515  0.          0.40584515  0.74153119
  0.94910791]
-> Pesos:
[0.12948497 0.27970539 0.38183005 0.41795918 0.38183005 0.27970539
 0.12948497]


REGRA DE 8 PONTO(S):
-> Pontos:
[-0.96028986 -0.79666648 -0.52553241 -0.18343464  0.18343464  0.52553241
  0.79666648  0.96028986]
-> Pesos:
[0.10122854 0.22238103 0.31370665 0.36268378 0.36268378 0.31370665
 0.22238103 0.10122854]


REGRA DE 9 PONTO(S):
-> Pontos:
[-0.96816024 -0.83603111 -0.61337143 -0.32425342  0.          0.32425342
  0.61337143  0.83603111  0.96816024]
-> Pesos:
[0.08127439 0.18064816 0.2606107  0.31234708 0.33023936 0.31234708
 0.2606107  0.18064816 0.08127439]


REGRA DE 10 PONTO(S):
-> Pontos:
[-0.97390653 -0.86506337 -0.67940957 -0.43339539 -0.14887434  0.14887434
  0.43339539  0.67940957  0.86506337  0.97390653]
-> Pesos:
[0.06667134 0.14945135 0.21908636 0.26926672 0.29552422 0.29552422
 0.26926672 0.21908636 0.14945135 0.06667134]


REGRA DE 11 PONTO(S):
-> Pontos:
[-0.97822866 -0.8870626  -0.73015201 -0.51909613 -0.26954316  0.
  0.26954316  0.51909613  0.73015201  0.8870626   0.97822866]
-> Pesos:
[0.05566857 0.12558037 0.18629021 0.23319376 0.26280454 0.27292509
 0.26280454 0.23319376 0.18629021 0.12558037 0.05566857]


REGRA DE 12 PONTO(S):
-> Pontos:
[-0.98156063 -0.90411726 -0.76990267 -0.58731795 -0.3678315  -0.12523341
  0.12523341  0.3678315   0.58731795  0.76990267  0.90411726  0.98156063]
-> Pesos:
[0.04717534 0.10693933 0.16007833 0.20316743 0.23349254 0.24914705
 0.24914705 0.23349254 0.20316743 0.16007833 0.10693933 0.04717534]


REGRA DE 13 PONTO(S):
-> Pontos:
[-0.98418305 -0.9175984  -0.80157809 -0.64234934 -0.44849275 -0.23045832
  0.          0.23045832  0.44849275  0.64234934  0.80157809  0.9175984
  0.98418305]
-> Pesos:
[0.040484   0.0921215  0.13887351 0.17814598 0.20781605 0.22628318
 0.23255155 0.22628318 0.20781605 0.17814598 0.13887351 0.0921215
 0.040484  ]


REGRA DE 14 PONTO(S):
-> Pontos:
[-0.98628381 -0.92843488 -0.82720132 -0.6872929  -0.51524864 -0.31911237
 -0.10805495  0.10805495  0.31911237  0.51524864  0.6872929   0.82720132
  0.92843488  0.98628381]
-> Pesos:
[0.03511946 0.08015809 0.12151857 0.15720317 0.1855384  0.20519846
 0.21526385 0.21526385 0.20519846 0.1855384  0.15720317 0.12151857
 0.08015809 0.03511946]


REGRA DE 15 PONTO(S):
-> Pontos:
[-0.98799252 -0.93727339 -0.84820658 -0.72441773 -0.57097217 -0.39415135
 -0.20119409  0.          0.20119409  0.39415135  0.57097217  0.72441773
  0.84820658  0.93727339  0.98799252]
-> Pesos:
[0.03075324 0.07036605 0.10715922 0.13957068 0.16626921 0.186161
 0.19843149 0.20257824 0.19843149 0.186161   0.16626921 0.13957068
 0.10715922 0.07036605 0.03075324]


REGRA DE 16 PONTO(S):
-> Pontos:
[-0.98940093 -0.94457502 -0.8656312  -0.75540441 -0.61787624 -0.45801678
 -0.28160355 -0.09501251  0.09501251  0.28160355  0.45801678  0.61787624
  0.75540441  0.8656312   0.94457502  0.98940093]
-> Pesos:
[0.02715246 0.06225352 0.09515851 0.12462897 0.14959599 0.16915652
 0.18260342 0.18945061 0.18945061 0.18260342 0.16915652 0.14959599
 0.12462897 0.09515851 0.06225352 0.02715246]

A partir daí, podemos organizar uma tabela para a regra de até 8 pontos/pesos como segue:

# número máximo de pontos
N = 8

header='| Regra | nó(s) | peso(s) |\n|---|---|---|'
print(header)
for i in range(1,N+1):
    (pontos,pesos) = leg.leggauss(i)       
    p = ', '.join([str(p) for p in pontos])
    w = ', '.join([str(p) for p in pesos])    
    row = '|' + str(i) + '|' + p + '|' + w + '|'
    print(row)                   

| Regra | nó(s) | peso(s) |
|---|---|---|
|1|0.0|2.0|
|2|-0.5773502691896257, 0.5773502691896257|1.0, 1.0|
|3|-0.7745966692414834, 0.0, 0.7745966692414834|0.5555555555555557, 0.8888888888888888, 0.5555555555555557|
|4|-0.8611363115940526, -0.33998104358485626, 0.33998104358485626, 0.8611363115940526|0.3478548451374537, 0.6521451548625462, 0.6521451548625462, 0.3478548451374537|
|5|-0.906179845938664, -0.5384693101056831, 0.0, 0.5384693101056831, 0.906179845938664|0.23692688505618942, 0.4786286704993662, 0.568888888888889, 0.4786286704993662, 0.23692688505618942|
|6|-0.932469514203152, -0.6612093864662645, -0.23861918608319693, 0.23861918608319693, 0.6612093864662645, 0.932469514203152|0.17132449237916975, 0.36076157304813894, 0.46791393457269137, 0.46791393457269137, 0.36076157304813894, 0.17132449237916975|
|7|-0.9491079123427585, -0.7415311855993945, -0.4058451513773972, 0.0, 0.4058451513773972, 0.7415311855993945, 0.9491079123427585|0.12948496616887065, 0.2797053914892766, 0.3818300505051183, 0.41795918367346896, 0.3818300505051183, 0.2797053914892766, 0.12948496616887065|
|8|-0.9602898564975362, -0.7966664774136267, -0.525532409916329, -0.18343464249564978, 0.18343464249564978, 0.525532409916329, 0.7966664774136267, 0.9602898564975362|0.10122853629037669, 0.22238103445337434, 0.31370664587788705, 0.36268378337836177, 0.36268378337836177, 0.31370664587788705, 0.22238103445337434, 0.10122853629037669|

23.3.1.1. Tabela de quadratura de Gauss-Legendre#

Regra

nó(s)

peso(s)

1

0.0

2.0

2

-0.57735026919, 0.57735026919

1.0, 1.0

3

-0.774596669241, 0.0, 0.774596669241

0.555555555556, 0.888888888889, 0.555555555556

4

-0.861136311594, -0.339981043585, 0.339981043585, 0.861136311594

0.347854845137, 0.652145154863, 0.652145154863, 0.347854845137

5

-0.906179845939, -0.538469310106, 0.0, 0.538469310106, 0.906179845939

0.236926885056, 0.478628670499, 0.568888888889, 0.478628670499, 0.236926885056

6

-0.932469514203, -0.661209386466, -0.238619186083, 0.238619186083, 0.661209386466, 0.932469514203

0.171324492379, 0.360761573048, 0.467913934573, 0.467913934573, 0.360761573048, 0.171324492379

7

-0.949107912343, -0.741531185599, -0.405845151377, 0.0, 0.405845151377, 0.741531185599, 0.949107912343

0.129484966169, 0.279705391489, 0.381830050505, 0.417959183673, 0.381830050505, 0.279705391489, 0.129484966169

8

-0.960289856498, -0.796666477414, -0.525532409916, -0.183434642496, 0.183434642496, 0.525532409916, 0.796666477414, 0.960289856498

0.10122853629, 0.222381034453, 0.313706645878, 0.362683783378, 0.362683783378, 0.313706645878, 0.222381034453, 0.10122853629

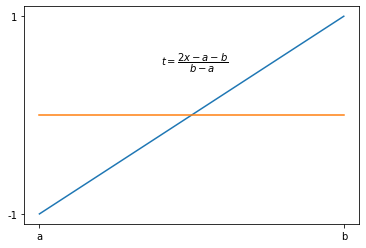
23.4. Transformação de variáveis#

Uma integral \(\int_a^b f(x) \, dx\) sobre \([a,b]\) arbitrário ser transformada em uma integral em \([-1,1]\) utilizando a mudança de variáveis:

\[t = \dfrac{2x - a - b}{b - a} \Rightarrow x = \dfrac{1}{2}[(b-a)t + a + b]\]
x = np.linspace(2,4)
y = x - 3
plt.plot(x,y);
plt.plot(x,x*0);
plt.xticks([2,4],['a','b']);
plt.yticks([-1,1],['-1','1']);
plt.annotate('$t = \dfrac{2x - a - b}{b - a}$',(2.8,0.5));
_images/aula-19-quadratura-gaussiana_19_0.png

23.4.1. Tarefa#

Defina uma função como a seguinte que retorne output, tal que type(output) seja str.

def print_gauss_legendre_table(N):
    header='| Regra | nó(s) | peso(s) |\n|---|---|---|'
    print(header)
    for i in range(1,N+1):
        (pontos,pesos) = leg.leggauss(i)       
        p = ', '.join([str(p) for p in pontos])
        w = ', '.join([str(p) for p in pesos])    
        row = '|' + str(i) + '|' + p + '|' + w + '|'
        print(row)

Então, reimprima a tabela para 8 pesos/pontos anterior com o código.

output = print_gauss_legendre_table(8)

Em seguida, use o código abaixo para converter a saída da célula de código do Jupyter diretamente para Markdown.

from IPython.display import display, Markdown
display(Markdown(output))

Por último, incorpore esta funcionalidade em print_gauss_legendre_table(N), para N dado.

Regra

nó(s)

peso(s)

1

0.0

2.0

2

-0.57735026919, 0.57735026919

1.0, 1.0

3

-0.774596669241, 0.0, 0.774596669241

0.555555555556, 0.888888888889, 0.555555555556

4

-0.861136311594, -0.339981043585, 0.339981043585, 0.861136311594

0.347854845137, 0.652145154863, 0.652145154863, 0.347854845137

5

-0.906179845939, -0.538469310106, 0.0, 0.538469310106, 0.906179845939

0.236926885056, 0.478628670499, 0.568888888889, 0.478628670499, 0.236926885056

6

-0.932469514203, -0.661209386466, -0.238619186083, 0.238619186083, 0.661209386466, 0.932469514203

0.171324492379, 0.360761573048, 0.467913934573, 0.467913934573, 0.360761573048, 0.171324492379

7

-0.949107912343, -0.741531185599, -0.405845151377, 0.0, 0.405845151377, 0.741531185599, 0.949107912343

0.129484966169, 0.279705391489, 0.381830050505, 0.417959183673, 0.381830050505, 0.279705391489, 0.129484966169

8

-0.960289856498, -0.796666477414, -0.525532409916, -0.183434642496, 0.183434642496, 0.525532409916, 0.796666477414, 0.960289856498

0.10122853629, 0.222381034453, 0.313706645878, 0.362683783378, 0.362683783378, 0.313706645878, 0.222381034453, 0.10122853629

9

-0.968160239508, -0.836031107327, -0.613371432701, -0.324253423404, 0.0, 0.324253423404, 0.613371432701, 0.836031107327, 0.968160239508

0.0812743883616, 0.180648160695, 0.260610696403, 0.31234707704, 0.330239355001, 0.31234707704, 0.260610696403, 0.180648160695, 0.0812743883616

10

-0.973906528517, -0.865063366689, -0.679409568299, -0.433395394129, -0.148874338982, 0.148874338982, 0.433395394129, 0.679409568299, 0.865063366689, 0.973906528517

0.0666713443087, 0.149451349151, 0.219086362516, 0.26926671931, 0.295524224715, 0.295524224715, 0.26926671931, 0.219086362516, 0.149451349151, 0.0666713443087

11

-0.978228658146, -0.887062599768, -0.730152005574, -0.519096129207, -0.269543155952, 0.0, 0.269543155952, 0.519096129207, 0.730152005574, 0.887062599768, 0.978228658146

0.0556685671162, 0.125580369465, 0.186290210928, 0.233193764592, 0.26280454451, 0.272925086778, 0.26280454451, 0.233193764592, 0.186290210928, 0.125580369465, 0.0556685671162

12

-0.981560634247, -0.90411725637, -0.769902674194, -0.587317954287, -0.367831498998, -0.125233408511, 0.125233408511, 0.367831498998, 0.587317954287, 0.769902674194, 0.90411725637, 0.981560634247

0.0471753363865, 0.106939325995, 0.160078328543, 0.203167426723, 0.233492536538, 0.249147045813, 0.249147045813, 0.233492536538, 0.203167426723, 0.160078328543, 0.106939325995, 0.0471753363865