Code Session 7: Ajuste de Curvas#

import numpy as np 
import matplotlib.pyplot as plt 
import matplotlib as mpl

mpl.rcParams['figure.figsize'] = (6,4)

Regressão Linear#

linregress#

A regressão linear é o modelo mais básico para realizar ajuste de dados e frequentemente aplicado em estudos estatísticos. Em Python, a regressão linear pode ser realizada com a função linregress. Esta função calcula a regressão linear por mínimos quadrados (a rigor, o termo deveria ser traduzido como quadrados mínimos) para dois conjuntos de medição.

Os argumentos de entrada obrigatórios desta função são:

  1. o primeiro conjunto de dados x (lista ou objeto tipo array)

  2. o segundo conjunto de dados y (lista ou objeto tipo array)

Os argumentos de saída principais são

  • slope: coeficiente angular da reta obtida pela regressão linear

  • intercept: coeficiente linear da reta obtida pela regressão linear

  • rvalue: valor do coeficiente de correlação

  • pvalue: valor-p do teste de hipótese

Por enquanto, desconsideraremos o valor-p.

Nota: para obter o valor do coeficiente de determinação \(R^2\), o valor de rvalue deve ser elevado ao quadrado, i.e. R2 = rvalue**2.

Como importar a função?

from scipy.stats import linregress

Problema 1#

A tabela a seguir lista a massa \(M\) e o consumo médio \(C\) de automóveis fabricados pela Ford e Honda em 2008. Faça um ajuste linear \(C = b + aM\) aos dados e calcule o desvio padrão.

modelo

massa (kg)

C (km/litro)

Focus

1198

11.90

Crown Victoria

1715

6.80

Expedition

2530

5.53

Explorer

2014

6.38

F-150

2136

5.53

Fusion

1492

8.50

Taurus

1652

7.65

Fit

1168

13.60

Accord

1492

9.78

CR-V

1602

8.93

Civic

1192

11.90

Ridgeline

2045

6.38

Nota: esta tabela está disponível em formato .csv no arquivo file-cs7-autos.csv.

Resolução#

cat '../file-cs7-autos.csv'

modelo,massa (kg),C (km/litro)
Focus,1198,11.90
Crown Victoria,1715,6.80
Expedition,2530,5.53
Explorer,2014,6.38
F-150,2136,5.53
Fusion,1492,8.50
Taurus,1652,7.65
Fit,1168,13.60
Accord,1492,9.78
CR-V,1602,8.93
Civic,1192,11.90
Ridgeline,2045,6.38

Vamos ler o arquivo de dados e converter diretamente a matriz de dados em dois arrays, um para valores de massa e outro para consumo.

M, C = np.loadtxt(fname='../file-cs7-autos.csv', # nome do arquivo
                  delimiter=',', # separador dos dados
                  skiprows=1, # ignora 1a. linha do arquivo
                  usecols=(1,2), # lê apenas 2a. e 3a. colunas
                  unpack=True # desempactamento
                  )

Em seguida, fazemos a regressão linear:

a, b, R, _, _ = linregress(M,C)
print(f'Regressão linear executada com a = {a:.3f}, b = {b:.3f} e R2 = {R*R:.2f}')

Regressão linear executada com a = -0.006, b = 18.410 e R2 = 0.83

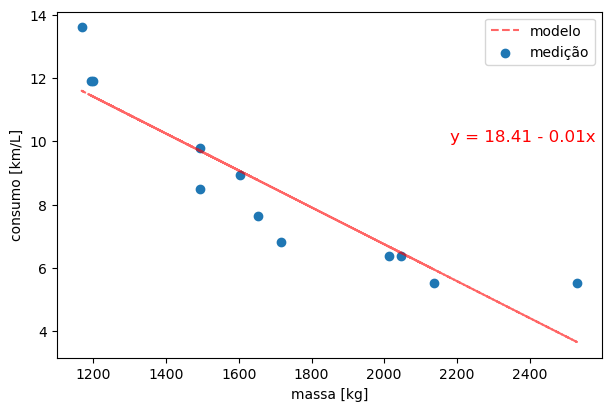
Enfim, podemos visualizar o resultado:

# ajuste
C2 = a*M + b

# figura
fig, ax = plt.subplots(constrained_layout=True)
ax.plot(M,C2,'r--',alpha=0.6,label='modelo')
ax.scatter(M,C,label='medição')
ax.legend()
ax.set_xlabel('massa [kg]')
ax.set_ylabel('consumo [km/L]')
ax.annotate(f'y = {b:.2f} - {-a:.2f}x',
            (2180,10),
            fontsize=12,
            c='r');
../_images/codeSession-7-fit_12_0.png

Medindo o desvio padrão do ajuste por mínimos quadrados#

Para calcular o desvio padrão do ajuste, precisamos reconhecer o número de amostras \(n\), o número de parâmetros do modelo de ajuste \(m\) e calcular a soma \(S\) dos quadrados. A fórmula utilizada é a seguinte:

\[\sigma = \sqrt{ \dfrac{S}{n-m} },\]

onde \(S = \sum\limits_{k=0}^n [y_i - \phi(x_i)]^2\).

Notemos que se \(n = m\) (caso da interpolação), \(\sigma = \infty\), i.e. seria indefinido, já que o denominador anular-se-ia.

O modelo de ajuste \(\phi(x)\) é considerado polinomial. Então, no caso da regressão linear, temos apenas 2 parâmetros: o coeficiente linear e o angular.

Sabemos que \(m=2\). Agora, resta usar \(n\) e calcular \(S\). Isto é tudo de que precisamos para calcular \(\sigma\) para o nosso problema.

n = M.size # número de amostras
m = 2 # número de parâmetros
print(f'n = {n:.0f}')

n = 12

O cálculo de \(S\) pode ser feito da seguinte maneira:

S = np.dot(C - C2, C - C2) # soma dos quadrados (resíduos)
print(f'S = {S:.3f}')

S = 13.553

Enfim, \(\sigma\) será dado por:

sigma = np.sqrt(S/(n-m)) # desvio padrão
print(f'σ = {sigma:.3f}')

σ = 1.164

Ajuste polinomial (linear)#

O ajuste de formas lineares de ordem superior (polinomial) pode ser realizado por meio da função polyfit.

polyfit#

Esta função ajusta um polinômio de grau \(g\) à tabela de dados.

Os argumentos de entrada obrigatórios desta função são:

  1. o primeiro conjunto de dados x (lista ou objeto tipo array)

  2. o segundo conjunto de dados y (lista ou objeto tipo array)

  3. o grau do polinômio g

O principal argumento de saída é:

  • p: lista dos g+1 coeficientes do modelo (ordenados do maior para o menor grau)

Como importá-la?

from numpy import polyfit

Como já importamos o numpy, basta chamar a função com:

np.polyfit(x,y,deg)

Problema 2#

Refaça o Problema 1 ajustando os dados com polinômios de grau 2, 3, 4 e 5 e plote os gráficos dos modelos ajustados aos dados em apenas uma figura.

Resolução#

Uma vez que já temos as variáveis armazenadas na memória, basta criarmos os ajustes.

p2 = np.polyfit(M,C,2)
p3 = np.polyfit(M,C,3) 
p4 = np.polyfit(M,C,4) 
p5 = np.polyfit(M,C,5)

Nota: o código abaixo realiza o mesmo, de forma compacta.

for g in range(2,6):
    exec(f'p{g} = np.polyfit(M,C,g)')

Para imprimir a lista dos coeficientes, basta fazer:

for p in [p2, p3, p4, p5]:
    print(*p, sep=', ', end='\n')

5.26020025147925e-06, -0.024582932608248086, 34.199195235449906
-1.8913566501289084e-09, 1.5605099762465975e-05, -0.04275565798726278, 44.427911273714024
3.371763317273691e-12, -2.6652321095782617e-08, 8.210414248684593e-05, -0.12006675173298169, 77.22226942351008
-3.128534116773908e-14, 2.8613273579644486e-10, -1.0320518728742421e-06, 0.001839906143292905, -1.6309631822598512, 587.8122971513164

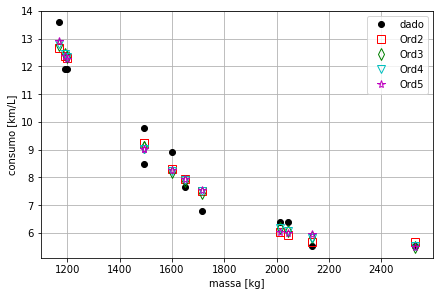
Para plotarmos as curvas, devemos nos atentar para o grau dos modelos. Podemos criá-las da seguinte forma:

# modelos
C22 = p2[0]*M**2 + p2[1]*M    + p2[2] # modelo quadrático
C23 = p3[0]*M**3 + p3[1]*M**2 + p3[2]*M    + p3[3] # modelo cúbico
C24 = p4[0]*M**4 + p4[1]*M**3 + p4[2]*M**2 + p4[3]*M    + p4[4] # modelo de quarta ordem
C25 = p5[0]*M**5 + p5[1]*M**4 + p5[2]*M**3 + p5[3]*M**2 + p5[4]*M + p5[5] # modelo de quinta ordem

# plotagem
fig, ax = plt.subplots(constrained_layout=True)
ax.grid(True)

ax.plot(M,C,  'ko',ms=6, mfc='black', label='dado') 
ax.plot(M,C22,'rs',ms=8, mfc='None', label='Ord2') 
ax.plot(M,C23,'gd',ms=8, mfc='None', label='Ord3')
ax.plot(M,C24,'cv',ms=8, mfc='None', label='Ord4')
ax.plot(M,C25,'m*',ms=8, mfc='None', label='Ord5') 

ax.set_xlabel('massa [kg]')
ax.set_ylabel('consumo [km/L]')
ax.legend(loc='best');
../_images/codeSession-7-fit_28_0.png

Exercício complementar#

Escreva uma função genérica que recebe a tabela de dados e o grau do modelo polinomial de ajuste e retorna os coeficientes do modelo, o desvio padrão do ajuste e os gráficos de dispersão conjuntamente com os dos modelos de ajuste.

Problema 3#

A intensidade de radiação de uma substância radioativa foi medida em intervalos semestrais. A tabela de valores está disponível no arquivo file-cs7-radiacao.csv, onte \(t\) é o tempo e \(\gamma\) é a intensidade relativa de radiação. Sabendo que a radioatividade decai exponencialmente com o tempo, \(\gamma(t) = ate^{-bt}\), estime a meia-vida radioativa (tempo no qual \(\gamma\) atinge metade de seu valor) da substância.

Resolução#

Primeiramente, vamos ler o arquivo.

t, g = np.loadtxt(fname='../file-cs7-radiacao.csv',
                   delimiter=',',
                   skiprows=1,
                   unpack=True)

t,g

(array([0.5, 1. , 1.5, 2. , 2.5]), array([0.541, 0.398, 0.232, 0.106, 0.052]))

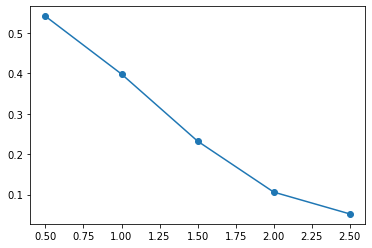
Agora, vamos plotar os dados apenas para verificar o comportamento da dispersão.

plt.plot(t,g,'o-');
../_images/codeSession-7-fit_36_0.png

Teste de alinhamento#

Para ajustarmos um modelo não-linear à exponencial, antes precisamos convertê-la a uma forma linear, ou seja, linearizá-la. Para isso, aplicamos \(\log\) (nome da função logaritmo natural em Python) em ambos os lados da função. Ao deslocar o termo \(t\) fora da exponencial para o lado esquerdo da equação, teremos:

\[\log\left(\frac{\gamma}{t}\right) = \log(a) - bt\]

Definindo \(z = \log(\frac{\gamma}{t})\), \(x = \log(a)\), podemos agora fazer uma regressão linear nas variáveis \(t\) e \(z\) para o modelo

\[z = x - bt\]

Agora, plotando a dispersão no plano \((t,z)\), verificamos se a curva é aproximadamente uma reta.

z = np.log(g/t)
plt.plot(t,z);
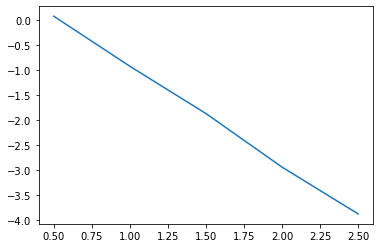
../_images/codeSession-7-fit_38_0.png

Como se vê, o teste de alinhamento mostra que a função exponencial é um modelo não-linear satisfatório para modelar o comportamento físico em questão.

Computando a regressão linear, temos:

b,x,R,_,_ = linregress(t,z)
print(f'Regressão linear executada com inclinação = {b:.3f}, interceptação = {x:.3f} e R2 = {R*R:.2f}')

Regressão linear executada com inclinação = -1.984, interceptação = 1.072 e R2 = 1.00

Vemos que, de fato, as variáveis têm uma altíssima correlação, visto que \(R^2 \approx 1\). Agora, para plotar o modelo de ajuste, recuperamos o valor de \(a\) operando inversamente e o usamos na curva do modelo para comparar com os dados experimentais.

a = np.exp(x); # recuperando parâmetro de ajuste
mod = lambda t: a*t*np.exp(b*t)

plt.plot(t,g,'o',mfc="None");
plt.plot(t,mod(t),'o',mfc="None");
plt.legend(('experimento','ajuste'));
../_images/codeSession-7-fit_43_0.png

O modelo está bem ajustado. Para estimar a meia-vida da substância, devemos encontrar o instante de tempo \(t_m\) tal que \(\gamma(t_m) = 0.5\gamma_0\). Então, notemos que:

\[\gamma(t_m) = at_me^{-bt_m} \Rightarrow 0.5\gamma_0 = at_me^{-bt_m}\]

Todavia, não conseguimos uma relação explícita para \(t_m\), fato que nos leva a resolver um segundo problema de determinação de raízes do tipo \(f(t_m) = 0\) com

\[f(t_m) = at_me^{-bt_m} - 0.5\gamma_0\]

Vamos resolver este problema usando a função fsolve do módulo scipy.optimize, mas antes precisamos passar a ela uma estimativa inicial. Rapidamente, façamos uma análise gráfica da curva \(f(t_m)\) para \(t_m = [0,2]\) (este intervalo é obtido após algumas plotagens prévias).

f = lambda tm: mod(tm) - 0.5*g[0]
ttm = np.linspace(0,2)
plt.plot(ttm,f(ttm),ttm,0*f(ttm));
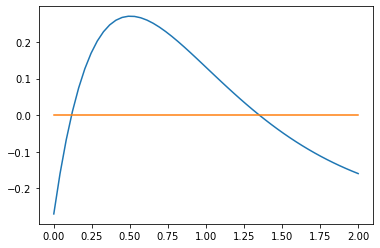
../_images/codeSession-7-fit_46_0.png

Existem duas raízes no intervalo. Porém, observando os valores tabelados de \(t\), é fácil ver que o valor para a condição inicial deve ser maior do que \(t_0 = 0.5\) e, portanto, mais próximo da segunda raiz no gráfico. Então, escolhamos para fsolve o valor inicial de \(t_m^0 = 1.25\).

from scipy.optimize import fsolve 

tm = fsolve(f,1.25)
print(f'Meia-vida localizada em tm = {tm[0]:.3f}.')

Meia-vida localizada em tm = 1.351.

Uma última verificação mostra que este valor de \(t_m\) é condizente com os dados experimentais, pois o seguinte erro é pequeno.

mod(tm) - 0.5*g[0]

array([1.11022302e-16])