Code Session 8: Integração#

import numpy as np 
import matplotlib.pyplot as plt

A integração numérica em uma variável pode ser realizada em Python utilizando a função quad do módulo scipy.integrate.

quad#

Esta função calcula a integral definida \(\int_a^b f(x) \, dx\) numericamente através de regras de quadratura.

Os argumentos de entrada obrigatórios desta função são:

  1. a função f a ser integrada

  2. o limite inferior a

  3. o limite superior b

Os principais argumentos de saída são:

  • y: valor numérico da integral

  • abserr: estimativa do erro absoluto

Como importá-la?

from scipy.integrate import quad

from scipy.integrate import quad

Problema 1#

O período de um pêndulo simples de comprimento \(L\) é \(\tau = 4\sqrt{ \dfrac{L}{g} } h(\theta_0)\), onde \(g\) é a aceleração gravitacional, \(\theta_0\) representa a amplitude angular, e

\[h(\theta_0) = \int_0^{\pi/2} \dfrac{1}{ \sqrt{ 1 - \textrm{sen}^2(\theta_0/2)\textrm{sen}^2 \theta } } \, d\theta\]

Calcule \(h(\tau)\), para \(\tau = 15^{\circ}, \, 30^{\circ}, \, 45^{\circ}\) e compare estes valores com \(h(0^{\circ}) = \pi/2\) (a aproximação usada para pequenas amplitudes).

Resolução#

Em primeiro lugar, fazemos os cálculos diretos da integral para os distintos valores de \(\tau\).

# cálculo direto das integrais caso a caso

theta0 = np.array([0,15,30,45]) # ângulos

vals,errs = [],[] # integrais, erros

for t in theta0:
    f = lambda theta: 1/(np.sqrt(1. - np.sin(t/2)**2 * np.sin(theta)**2))
    v,e = quad(f,0,np.pi/2)
    print(f'Integral h({t}) = {v:g}')
    vals.append(v)
    errs.append(e)

# converte listas para arrays
vals = np.asarray(vals)
errs = np.asarray(errs)

Integral h(0) = 1.5708
Integral h(15) = 2.49203
Integral h(30) = 1.79372
Integral h(45) = 1.67896

Vemos que o valor das integrais é muito sensível. Para realizar uma comparação mais interessante, utilizaremos um cálculo relativo tomando o valor em \(h(15)\) como referência.

plt.stem(theta0, (vals - vals[0])/vals[0], use_line_collection=True);
plt.xlabel('$\\theta_0$')
plt.ylabel('erro relativo');

/var/folders/ll/g0vl8b194pbfyp4cwpzz4p740000gn/T/ipykernel_51604/945931442.py:1: MatplotlibDeprecationWarning: The 'use_line_collection' parameter of stem() was deprecated in Matplotlib 3.6 and will be removed two minor releases later. If any parameter follows 'use_line_collection', they should be passed as keyword, not positionally.
  plt.stem(theta0, (vals - vals[0])/vals[0], use_line_collection=True);
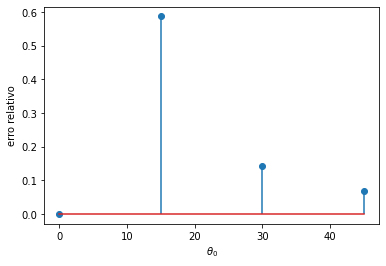
../_images/codeSession-8-integrate_8_1.png

Podemos verificar que a mudança de valor da integral entre \(15^{\circ}\) e \(30^{\circ}\) é da ordem de 60%, enquanto que nos demais casos, ela se limita a 20%.

Problema 2#

Uma corrente elétrica alternada é descrita por

\[i(t) = i_0 \left( \textrm{sen}\left( \frac{\pi t}{t_0} \right) - \beta \, \textrm{sen}\left( \frac{2 \pi t}{t_0} \right) \right),\]

onde \(i_0 = 1 \, A\), \(t_0 = 0.05 \, s\) e \(\beta =0.2\). Calcule a corrente RMS definida por

\[i_{rms} = \sqrt{ \dfrac{1}{t_0} \int_0^{t_0} i^2(t) \, dt}\]

Resolução#

Neste caso, basta passarmos os valores iniciais e finais para computar a integral.

i0, t0, beta = 1.0, 0.05, 0.2 # parâmetros iniciais

i2 = lambda t: ( i0 * ( np.sin( (np.pi*t) / t0 ) - beta * np.sin( (2*np.pi*t) / t0 ) ) )**2 # função

i_rms = np.sqrt( 1.0/t0 * quad(i2, 0, t0)[0] )

print(f'Corrente RMS = {i_rms:g} A')

Corrente RMS = 0.72111 A

Regra do Trapézio Generalizada#

A regra do trapézio generalizada (composta) pode ser calculada usando

scipy.integrate.cumtrapz

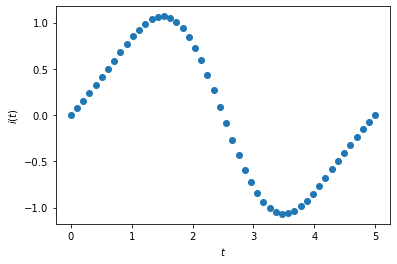
Vamos utilizar a função \(i(t)\) do Problema 2 e estimar sua integral no intervalo \(t = [0,5]\) utilizando a regra do trapézio generalizada.

# Visualização
t = np.linspace(0,5)
i = lambda t: i0 * ( np.sin( (np.pi*t) / t0 ) - beta * np.sin( (2*np.pi*t) / t0 ) )  # função

plt.plot(t,i(t),'o');
plt.xlabel('$t$')
plt.ylabel('$i(t)$');
../_images/codeSession-8-integrate_14_0.png 
from scipy.integrate import cumtrapz

i = lambda t: i0 * ( np.sin( (np.pi*t) / t0 ) - beta * np.sin( (2*np.pi*t) / t0 ) ) # função

T = cumtrapz(i(t), t)[-1] # pega último valor, já que é cumulativa

print(f'Integral por Trapézio = {T:g}')

Integral por Trapézio = -4.97605e-15

Quadratura Gaussiana (QG)#

O cálculo de uma integral por quadratura Gaussiana pode ser calculado usando

scipy.integrate.quadrature

Vamos utilizar a função \(i(t)\) do Problema 2 e estimar sua integral no intervalo \(t = [0,5]\) utilizando a QG para várias ordens (controladas pelo argumento miniter).

from scipy.integrate import quadrature

for ordem in range(1,11):
    I_QG,err_QG = quadrature(i,0,5,miniter=ordem)
    print(f'Integral por QG (ordem {ordem}) = {I_QG:g}')

Integral por QG (ordem 1) = 3.60822e-14
Integral por QG (ordem 2) = 9.71445e-15
Integral por QG (ordem 3) = 4.35416e-14
Integral por QG (ordem 4) = 6.92502e-14
Integral por QG (ordem 5) = 6.57807e-14
Integral por QG (ordem 6) = -5.7801e-14
Integral por QG (ordem 7) = -1.40166e-14
Integral por QG (ordem 8) = -1.60635e-14
Integral por QG (ordem 9) = -7.63278e-16
Integral por QG (ordem 10) = -4.0341e-14