32. Malhas numéricas

Ao transferir a informação de nossos modelos matemáticos do universo contínuo para o universo discreto do computador, precisamos criar uma malha numérica (a construção Cartesiana em gradeado recebe o nome de grade numérica), que pode ser estruturada por uma sucessão de pontos tal como uma imitação de uma reta “furada”. Em uma dimensão, uma malha numérica uniforme, cujo espaçamento entre seus pontos é igual, pode ser definida como uma progressão aritmética:

\[t_n = t_0 \pm n h, \ \ n = 1,2,\ldots,N,\]

onde \(h\) é conhecido como passo.

32.1. Malhas uniformes

A figura abaixo mostra os pontos de uma malha numérica uniforme. A linha pontilhada foi desenhada meramente para representar a porção do contínuo que o computador não captura, isto é, a informação que é perdida.

# desenha uma malha numerica uniforme

import numpy as np
import matplotlib.pyplot as plt 

# pontos
x = np.arange(9)
y = 0*x

# configuracoes
plt.figure(figsize=(6.4,0.5))
plt.plot(x,y,'ok',markersize=4)
plt.plot(x,y,':k',linewidth=1)
plt.ylim((-0.02,0.1))
plt.box(False)
locs, labels = plt.xticks()
plt.xticks(x, ('$t_{-N}$','$\ldots$','$t_{-2}$','$t_{-1}$','$t_{0}$','$t_{1}$','$t_{2}$','$\ldots$','$t_{N}$') )
plt.tick_params(axis='both',width=0.0,labelleft=False)

32.2. Malhas não uniformes

Uma malha numérica não uniforme é aquela para a qual o tamanho do passo não é constante, como vemos na Figura a seguir. Neste caso, podemos ter comprimentos arbitrários \(h_0 \neq h_1 \neq \ldots \neq h_{N-1}\) todos distintos, tanto à esquerda quanto à direita de \(t_0\).

# desenha uma malha numerica nao-uniforme

# pontos
x = np.array([-0.01,0.06,0.15,0.21,0.28,0.45,0.65,0.9,1.2])
y = 0*x

# configuracoes
plt.figure(figsize=(6.4,0.5))
plt.plot(x,y,'ok',markersize=4)
plt.plot(x,y,':k',linewidth=1)
plt.ylim((-0.02,0.1))
plt.box(False)
locs, labels = plt.xticks()
plt.xticks(x, ('$t_{-N}$','$\ldots$','$t_{-2}$','$t_{-1}$','$t_{0}$','$t_{1}$','$t_{2}$','$\ldots$','$t_{N}$') )
plt.tick_params(axis='both',width=0.0,labelleft=False)

32.3. Refinamento de malha

Quando uma malha não uniforme possui uma ou mais regiões onde há uma acumulação de pontos, dizemos que ela está refinada nessas regiões. Na figura, os pontos \(t_{-2}, t_{-1}\) e \(t_{0}\), por exemplo, acumulam-se próximos um do outro, ao passo que os pontos \(t_1, t_2\) e \(t_N\) afastam-se cada vez mais um do outro e da região de refinamento. Então, poderíamos dizer que a malha foi refinada entre \(t_{-2}\) e \(t_0\).

O refinamento faz mais sentido apenas quando queremos capturar informações localizadas com mais precisão. Esta situação ocorre, por exemplo, em problemas práticos que envolvem variações ou mudanças abruptas de propriedades, como é o caso da massa específica nas proximidades de uma interface de dois fluidos imiscíveis.

Nos esquemas acima, os nós com índice negativo são apenas ilustrativos e têm pouco efeito prático. Podemos trabalhar apenas com a indexação positiva sem problema algum.

32.4. Malha numérica bidimensional uniforme

Em particular, uma malha numérica bidimensional dependerá de cópias de arrays unidimensionais que formam as coordenadas do plano Cartesiano em cada dimensão

import numpy as np
import matplotlib.pyplot as plt

# limites do domínio:
# região do plano [a,b] x [c,d]
a, b = -4.0, 5.0
c, d = -2.0, 3.0

# no. de pontos em cada direção
nx, ny = 10, 20 

# distribuição dos pontos
x = np.linspace(a,b,nx)
y = np.linspace(c,d,ny)

# grade numérica 2D
[X,Y] = np.meshgrid(x,y)

# plotando pontos da grade numérica
plt.scatter(X,Y,s=3,c='k');
plt.title('Grade numérica 2D: pontos (x,y)')
plt.xlabel('x'); plt.ylabel('y');

32.4.1. Plotando curvas de nível

Plotaremos as curvas de nível 0 de funções não-lineares é útil para realizarmos análise gráfica e escolher vetores de estimativa inicial.

Para plotar curvas de nível das funções sobre a grade numérica anterior, fazemos o seguinte:

# funções definidas sobre a grade 2D
F = X**2 + Y**2 - 2
G = X**2 - Y**2 - 1

# contorno de nível 0
plt.contour(X,Y,F,colors='red',levels=0);
plt.contour(X,Y,G,colors='blue',levels=0);
plt.grid()

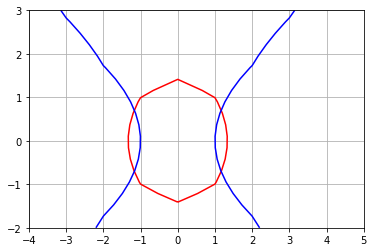
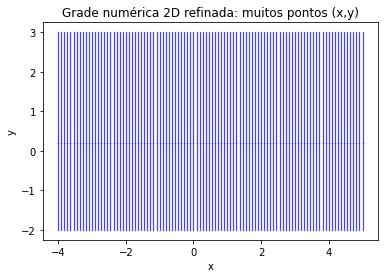
Por que a figura está meio “tosca”? Porque temos poucos pontos na grade. Vamos aumentar o número de pontos. Este processo é conhecido como refinamento de malha.

# refinando a malha numérica
nx2, ny2 = 100, 200

# redistribuição dos pontos
x2 = np.linspace(a,b,nx2)
y2 = np.linspace(c,d,ny2)

# grade numérica 2D refinada
[X2,Y2] = np.meshgrid(x2,y2)

# plotando pontos da grade numérica
plt.scatter(X2,Y2,s=0.1,c='b');
plt.title('Grade numérica 2D refinada: muitos pontos (x,y)')
plt.xlabel('x'); plt.ylabel('y');

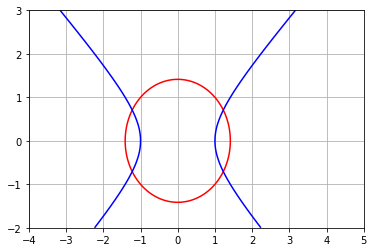
Vamos plotar novamente as curvas de nível das funções sobre a grade numérica refinada.

# funções definidas sobre a grade 2D refinada
F2 = X2**2 + Y2**2 - 2
G2 = X2**2 - Y2**2 - 1

# contorno de nível 0 na malha refinada
plt.contour(X2,Y2,F2,colors='red',levels=0);
plt.contour(X2,Y2,G2,colors='blue',levels=0);
plt.grid()