Método da Bisseção
Contents
5. Método da Bisseção#
O método da bisseção é uma das técnicas mais fundamentais para busca de raízes de equações não-lineares. Robusto e de fácil implementação, ele está estruturado no Teorema do Valor Intermediário, que afirma que se uma função contínua \(f(x)\) tem sinais opostos em dois pontos \(a\) e \(b\), condição que se verifica quando \(f(a) f(b) < 0\) é verdadeira, então existe pelo menos uma raiz da função no intervalo \([a, b]\). Em termos simples, o método envolve dividir repetidamente o intervalo ao meio e selecionar o subintervalo onde a raiz deve estar, baseando-se nos sinais de \(f\).
O método da bisseção tem garantia de convergência, desde que a função seja contínua e o intervalo inicial seja escolhido corretamente. No entanto, a convergência pode ser lenta em comparação com outros métodos, especialmente quando a função tem múltiplas raízes próximas. Neste capítulo, apresentaremos uma implementação caseira do método da bisseção para equações não-lineares unidimensionais. O algoritmo é capaz de lidar com as principais funções matemáticas da biblioteca numpy, possui alguns comandos para checagem de validade e usa a estrutura while para o laço do processo iterativo.

5.1. Implementação de alogoritmo#
Para ser executada, a função bissecao requer 5 parâmetros:
a função \(f(x)\) propriamente dita, representada por
f;o intervalo de busca da raiz \([a,b]\), representado pelas estimativas iniciais
aeb;o erro absoluto desejado \(EA_d\), representado por
e;o número máximo de iterações \(N\) para tentativa de solução, representado por
N.
import inspect, re
import numpy as np
from matplotlib.pyplot import plot
from warnings import warn
from prettytable import PrettyTable as pt
def bissecao(f,a,b,tol,N):
"""Algoritmo para determinação de raízes de equações não lineares
unidimensionais pelo método da bisseção.
Parâmetros:
f: string dependendo de uma variável, i.e., a função-alvo
(e.g., 'x**2 - 1', 'x**2*cos(x)', etc.)
a: estimativa inferior
b: estimativa superior
tol: erro desejado (tolerância)
N: número máximo de iterações a repetir
Retorno:
x: aproximação para a raiz da função
"""
# construtor de tabela
table = pt()
# substitui expressões da string pelas chamadas das funções do numpy
f = re.sub('(sin|sinh|cos|cosh|tan|tanh|exp|log|sqrt|log10|arcsin|arccos|arctan|arcsinh|arccosh|arctanh)', r'np.\1', f)
# identifica a variável independente
var = re.search(r'([a-zA-Z][\w]*) ?([\+\-\/*]|$|\))', f).group(1)
# cria função anônima
f = eval('lambda ' + var + ' :' + f)
# checa se a função é de uma variável, senão lança erro
if len(inspect.getfullargspec(f).args) - 1 > 0:
raise ValueError('O código é válido apenas para uma variável.')
# calcula valor da função nos extremos
fa = f(a)
fb = f(b)
# verifica sinal da função para o intervalo passado
if fa*fb >= 0:
raise ValueError('A função deve ter sinais opostos em a e b!')
# flag usada para marcar caso f(xm) = 0
done = False;
# no. iterações mínimo
niter = int(np.ceil(np.log((b-a)/tol)/np.log(2)))
if N < niter:
print(f'São necessárias pelo menos {niter} iterações, mas N = {N}.\n')
# cabeçalho de tabela
table.field_names = ['i','xm','f(xm)','a','b','f(a)','f(b)','EA']
# bisecta o intervalo
xm = (a+b)/2
# contador
i = 1
# loop
while abs(a-b) > tol and (not done and N != 0):
# avalia a função no ponto médio
fxm = f(xm)
# adiciona linha de tabela de resultado
table.add_row([i,np.round(xm,8),np.round(f(xm),8),
np.round(a,4),np.round(b,4),
np.round(f(a),4),np.round(f(b),4),
f'{abs(a-b):e}'])
if fa*fxm < 0: # Raiz esta à esquerda de xm
b = xm
fb = fxm
xm = (a+b)/2
elif fxm*fb < 0: # Raiz esta à direita de xm
a = xm
fa = fxm
xm = (a+b)/2
else: # Achamos a raiz
done = True
N -= 1 # Atualiza passo
i += 1 # Atualiza contador
# impressão de tabela
table.add_row([i,np.round(xm,8),np.round(f(xm),8),
np.round(a,4),np.round(b,4),
np.round(f(a),4),np.round(f(b),4),
f'{abs(a-b):e}'])
table.align = 'c'; print(table)
return xm
Note que o cerne desta função é o trecho abaixo. O resto do código é constituído de algumas especializações e comandos acessórios.
while abs(a-b) > tol and (not done and N != 0):
# avalia a função no ponto médio
fxm = f(xm)
if fa*fxm < 0: # Raiz esta à esquerda de xm
b = xm
fb = fxm
xm = (a+b)/2
elif fxm*fb < 0: # Raiz esta à direita de xm
a = xm
fa = fxm
xm = (a+b)/2
else: # Achamos a raiz
done = True
N -= 1 # Atualiza passo
i += 1 # Atualiza contador
5.2. Exemplos resolvidos#
Exemplo: Resolva o problema \(f(x) = 0\), para \(f(x) = -\text{arccos}(x) + 4\text{sen}(x) + 1.7\), no intervalo \(-0.2 \le x \le 1.0\) e \(\epsilon = 10^{-3}\).
Primeiramente, façamos uma análise gráfica para verificar o comportamento da função.
x = np.linspace(-0.2,1,100)
plot(x,-np.arccos(x) + 4*np.sin(x) + 1.7,'g',x,0*x,'k:');
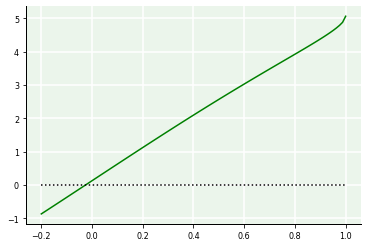
Uma vez que a raiz é única, basta aplicar o método que construímos à função desejada.
xm = bissecao('-arccos(x) + 4*sin(x) + 1.7',-0.2,1.0,1e-3,40)
+----+-------------+-------------+---------+---------+---------+--------+--------------+
| i | xm | f(xm) | a | b | f(a) | f(b) | EA |
+----+-------------+-------------+---------+---------+---------+--------+--------------+
| 1 | 0.4 | 2.09839389 | -0.2 | 1.0 | -0.8668 | 5.0659 | 1.200000e+00 |
| 2 | 0.1 | 0.62870476 | -0.2 | 0.4 | -0.8668 | 2.0984 | 6.000000e-01 |
| 3 | -0.05 | -0.12073386 | -0.2 | 0.1 | -0.8668 | 0.6287 | 3.000000e-01 |
| 4 | 0.025 | 0.25419586 | -0.05 | 0.1 | -0.1207 | 0.6287 | 1.500000e-01 |
| 5 | -0.0125 | 0.06670465 | -0.05 | 0.025 | -0.1207 | 0.2542 | 7.500000e-02 |
| 6 | -0.03125 | -0.02703107 | -0.05 | -0.0125 | -0.1207 | 0.0667 | 3.750000e-02 |
| 7 | -0.021875 | 0.01983391 | -0.0312 | -0.0125 | -0.027 | 0.0667 | 1.875000e-02 |
| 8 | -0.0265625 | -0.00359946 | -0.0312 | -0.0219 | -0.027 | 0.0198 | 9.375000e-03 |
| 9 | -0.02421875 | 0.00811703 | -0.0266 | -0.0219 | -0.0036 | 0.0198 | 4.687500e-03 |
| 10 | -0.02539062 | 0.00225873 | -0.0266 | -0.0242 | -0.0036 | 0.0081 | 2.343750e-03 |
| 11 | -0.02597656 | -0.00067038 | -0.0266 | -0.0254 | -0.0036 | 0.0023 | 1.171875e-03 |
| 12 | -0.02568359 | 0.00079417 | -0.026 | -0.0254 | -0.0007 | 0.0023 | 5.859375e-04 |
+----+-------------+-------------+---------+---------+---------+--------+--------------+
A raiz aproximada \(x^{*}\), tal que para \(f(x^{*}) = 0\) no intervalo-alvo é mostrada na última linha da tabela. Isto é,
# raiz aproximada
xm
-0.02568359375
Exemplo: Resolva o problema \(h(z) = 0\), para \(h(z) = -z(1-2z)^{-1} - \text{tan}(z+1)\), no intervalo \([1,8]\) e \(\epsilon = 10^{-5}\).
Primeiramente, façamos uma análise gráfica para verificar o comportamento da função.
z = np.linspace(1,8.5,100)
plot(z,z/(1 - 2*z) - np.tan(z+1),'g',z,0*z,'k:');
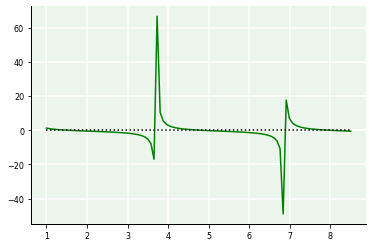
Neste caso, a função apresenta sensibilidades e mais de uma raiz no intervalo dado. Vamos buscar a raiz que está no subintervalo \([4,6]\). Para tanto, vamos deamplificar a plotagem.
z = np.linspace(4,6,100)
plot(z,z/(1 - 2*z) - np.tan(z+1),'g',z,0*z,'k:');
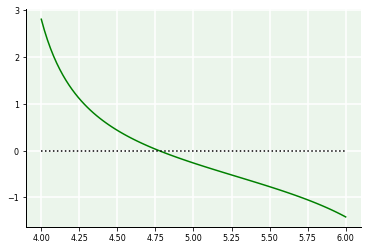
Uma vez que a raiz é única, basta aplicar o método que construímos à função desejada.
zm = bissecao('z/(1 - 2*z) - tan(z+1)',4,6,1e-5,20)
+----+------------+-------------+--------+--------+--------+---------+--------------+
| i | xm | f(xm) | a | b | f(a) | f(b) | EA |
+----+------------+-------------+--------+--------+--------+---------+--------------+
| 1 | 5.0 | -0.26454936 | 4 | 6 | 2.8091 | -1.4169 | 2.000000e+00 |
| 2 | 4.5 | 0.43308405 | 4 | 5.0 | 2.8091 | -0.2645 | 1.000000e+00 |
| 3 | 4.75 | 0.03138032 | 4.5 | 5.0 | 0.4331 | -0.2645 | 5.000000e-01 |
| 4 | 4.875 | -0.12466745 | 4.75 | 5.0 | 0.0314 | -0.2645 | 2.500000e-01 |
| 5 | 4.8125 | -0.04914268 | 4.75 | 4.875 | 0.0314 | -0.1247 | 1.250000e-01 |
| 6 | 4.78125 | -0.00957612 | 4.75 | 4.8125 | 0.0314 | -0.0491 | 6.250000e-02 |
| 7 | 4.765625 | 0.01071879 | 4.75 | 4.7812 | 0.0314 | -0.0096 | 3.125000e-02 |
| 8 | 4.7734375 | 0.00052675 | 4.7656 | 4.7812 | 0.0107 | -0.0096 | 1.562500e-02 |
| 9 | 4.77734375 | -0.00453568 | 4.7734 | 4.7812 | 0.0005 | -0.0096 | 7.812500e-03 |
| 10 | 4.77539062 | -0.00200723 | 4.7734 | 4.7773 | 0.0005 | -0.0045 | 3.906250e-03 |
| 11 | 4.77441406 | -0.00074094 | 4.7734 | 4.7754 | 0.0005 | -0.002 | 1.953125e-03 |
| 12 | 4.77392578 | -0.00010727 | 4.7734 | 4.7744 | 0.0005 | -0.0007 | 9.765625e-04 |
| 13 | 4.77368164 | 0.0002097 | 4.7734 | 4.7739 | 0.0005 | -0.0001 | 4.882812e-04 |
| 14 | 4.77380371 | 5.12e-05 | 4.7737 | 4.7739 | 0.0002 | -0.0001 | 2.441406e-04 |
| 15 | 4.77386475 | -2.803e-05 | 4.7738 | 4.7739 | 0.0001 | -0.0001 | 1.220703e-04 |
| 16 | 4.77383423 | 1.158e-05 | 4.7738 | 4.7739 | 0.0001 | -0.0 | 6.103516e-05 |
| 17 | 4.77384949 | -8.23e-06 | 4.7738 | 4.7739 | 0.0 | -0.0 | 3.051758e-05 |
| 18 | 4.77384186 | 1.68e-06 | 4.7738 | 4.7738 | 0.0 | -0.0 | 1.525879e-05 |
| 19 | 4.77384567 | -3.27e-06 | 4.7738 | 4.7738 | 0.0 | -0.0 | 7.629395e-06 |
+----+------------+-------------+--------+--------+--------+---------+--------------+
A raiz aproximada \(z^{*}\), tal que para \(h(z^{*}) = 0\) é mostrada na última linha da tabela. Isto é,
# raiz aproximada
zm
4.773845672607422
Por fim, vamos aplicar nosso método da bisseção ao problema do paraquedista apresentado no capítulo introdutório para buscar o coeficiente de arrasto adequado para os parâmetros de projeto impostos.
Primeiramente, definiremos uma função para retornar a equação particular.
def eq_paraq(tempo,massa,vel,grav):
""" Define equação particular para cálculo de coeficiente de arrasto
em salto de paraquedista. (Ver introdução.)
Parâmetros:
tempo: duração de salto até velocidade terminal [s]
massa: massa do paraquedista [kg]
vel: velocidade terminal desejada [m/s]
grav: aceleração gravitacional ambiente [m/s**2]
Retorno:
f: expressão numérica para equação particular
do coeficiente de arrasto
"""
# variáveis simbólicas
from sympy import symbols, exp, lambdify
g,m,t,v,c = symbols('g,m,t,v,c')
# expressão geral
f = (g*m/c)*(1 - exp((-c/m)*t)) - v
# expressão particular com valores substituídos convertidos para str
fs = f.subs({'g':grav,'m':massa,'v':vel,'t':tempo})
# expressão simbólica convertida para expessão numérica
fn = lambdify(c,fs,"numpy")
# imprime para
print(f'Equação particular: f(c) = {fs}')
return (fs,fn)
Em seguida, inserimos valores de entrada para teste.
# parâmetros de entrada
tempo, massa, vel, grav = 12, 70, 42, 9.81
# equação particular
fs,fn = eq_paraq(tempo,massa,vel,grav)
Equação particular: f(c) = -42 + 686.7*(1 - exp(-6*c/35))/c
O próximo passo realiza a análise gráfica para localização do intervalo de aproximação da raiz.
c = np.linspace(1,20)
plot(c,fn(c),'g',c,0*c,'k:');
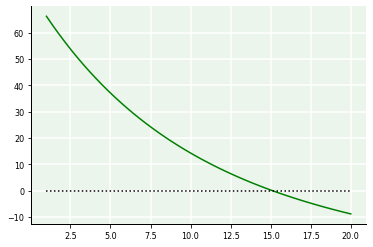
Encerrando, chamamos a função.
cm = bissecao(str(fs),14,17.0,1e-4,20)
+----+-------------+-------------+---------+---------+--------+---------+--------------+
| i | xm | f(xm) | a | b | f(a) | f(b) | EA |
+----+-------------+-------------+---------+---------+--------+---------+--------------+
| 1 | 15.5 | -0.80457281 | 14 | 17.0 | 2.6003 | -3.797 | 3.000000e+00 |
| 2 | 14.75 | 0.84203047 | 14 | 15.5 | 2.6003 | -0.8046 | 1.500000e+00 |
| 3 | 15.125 | 0.00533671 | 14.75 | 15.5 | 0.842 | -0.8046 | 7.500000e-01 |
| 4 | 15.3125 | -0.40289836 | 15.125 | 15.5 | 0.0053 | -0.8046 | 3.750000e-01 |
| 5 | 15.21875 | -0.19960925 | 15.125 | 15.3125 | 0.0053 | -0.4029 | 1.875000e-01 |
| 6 | 15.171875 | -0.09734443 | 15.125 | 15.2188 | 0.0053 | -0.1996 | 9.375000e-02 |
| 7 | 15.1484375 | -0.04605603 | 15.125 | 15.1719 | 0.0053 | -0.0973 | 4.687500e-02 |
| 8 | 15.13671875 | -0.02037272 | 15.125 | 15.1484 | 0.0053 | -0.0461 | 2.343750e-02 |
| 9 | 15.13085938 | -0.00752127 | 15.125 | 15.1367 | 0.0053 | -0.0204 | 1.171875e-02 |
| 10 | 15.12792969 | -0.0010931 | 15.125 | 15.1309 | 0.0053 | -0.0075 | 5.859375e-03 |
| 11 | 15.12646484 | 0.0021216 | 15.125 | 15.1279 | 0.0053 | -0.0011 | 2.929688e-03 |
| 12 | 15.12719727 | 0.0005142 | 15.1265 | 15.1279 | 0.0021 | -0.0011 | 1.464844e-03 |
| 13 | 15.12756348 | -0.00028946 | 15.1272 | 15.1279 | 0.0005 | -0.0011 | 7.324219e-04 |
| 14 | 15.12738037 | 0.00011237 | 15.1272 | 15.1276 | 0.0005 | -0.0003 | 3.662109e-04 |
| 15 | 15.12747192 | -8.855e-05 | 15.1274 | 15.1276 | 0.0001 | -0.0003 | 1.831055e-04 |
| 16 | 15.12742615 | 1.191e-05 | 15.1274 | 15.1275 | 0.0001 | -0.0001 | 9.155273e-05 |
+----+-------------+-------------+---------+---------+--------+---------+--------------+
Como se vê, o coeficiente de arrasto aproximado para este caso é dado por:
cm
15.127426147460938
5.3. Tarefas#
Repita a análise anterior alterando os parâmetros de projeto de salto para paraquedistas de diferentes massas e com duração de salto até a velocidade terminal variáveis. Faça a análise gráfica e busque aproximações.
Programe uma nova função para executar o método da falsa posição ou estenda o código anterior para uma nova função que contemple os dois casos (sugestão: use
if).
5.4. Problema proposto#
Uma reação química reversível \(2A+B \iff C\) pode ser caracterizada pela relação de equilíbrio \(K = \frac{c_c}{c_a^2c_b}\), onde \(c_i\) representa a concentração do constituinte \(i\). Suponha que:
\(x\) é o número de moles de \(C\) que são produzidos
a conservação da massa pode ser usada para reformular a relação de equilíbrio como \(K = \dfrac{(c_{c,0} + x)}{(c_{a,0} - 2x)^2 (c_{b,0} - x)}\), onde o subscrito \(0\) designa a concentração inicial de cada constituinte.
\(K = 0,016\), \(c_{a,0} = 42\), \(c_{b,0} = 28\) e \(c_{c,0} = 4\).
Dispondo dessas informações:
Faça a análise gráfica do modelo matemático do problema.
Defina o(s)intervalo(s) adequados(s) de localização da raiz.
Aplique o método da bisseção para determinar uma aproximação para \(x\) com erro inferior a \(10^{-5}\).

