Code Session 9: Método de Euler
Contents
Code Session 9: Método de Euler#
import numpy as np, matplotlib.pyplot as plt
A integração numérica de uma EDO pode ser realizada em Python utilizando a função solve_ivp do módulo scipy.integrate.
solve_ivp#
Esta função resolve um problema de valor inicial (PVI) para uma EDO ou um sistema de EDOs. Por padrão, o método de resolução é um algoritmo de Runge-Kutta com precisão de 4a. ordem.
Os argumentos de entrada obrigatórios desta função são:
a função
f(t,y)a ser integradao domínio de integração, definido como uma tupla
(t0,tf)a condição inicial
y0
O principal argumento de saída é um objeto sol, em que:
sol.t: retorna os valores do domíniosol.y: retorna os valores da solução numérica
from scipy.integrate import solve_ivp
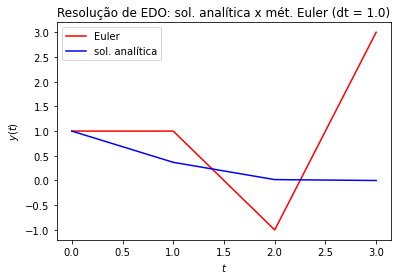
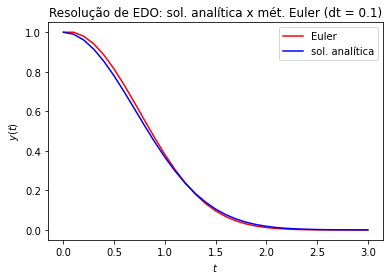
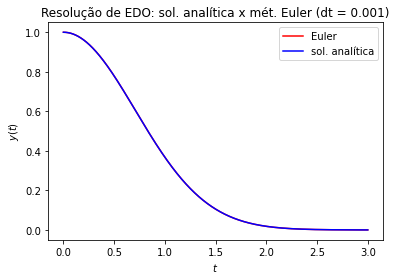
Exemplo: Resolver numericamente o PVI
para \(h=1.0,0.1,0.001\).
Compare a solução numérica com a analítica: \(y_{an}(t) = e^{-t^2}\).
f = lambda t,y: -2*y*t
yan = lambda t: np.exp(-t**2)
y0 = 1
a = 0.0
b = 3.0
T = [1.0,0.1,0.001]
for k in T:
t = np.arange(a, b+k, k)
y = solve_ivp(f, (a,b), [y0])
y2 = t*0
y2[0] = y0
dt = (b-a)/ (len(t)-1)
for i in range(0,len(t)-1):
y2[i+1] = y2[i] + f(t[i],y2[i])*dt
fig = plt.figure()
ax = fig.add_subplot(111)
#plt.plot(t,y,'k',label='odeint')
plt.plot(t,y2,'r',label='Euler')
plt.plot(t,yan(t),'b',label='sol. analítica')
plt.legend()
s = 'Resolução de EDO: sol. analítica x mét. Euler (dt = ' + str(k) + ')'
plt.title(s)
plt.xlabel('$t$')
plt.ylabel('$y(t)$')
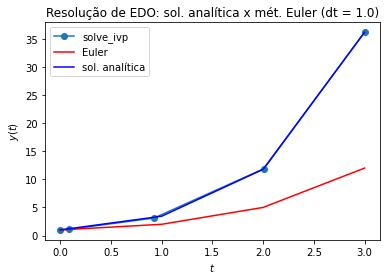
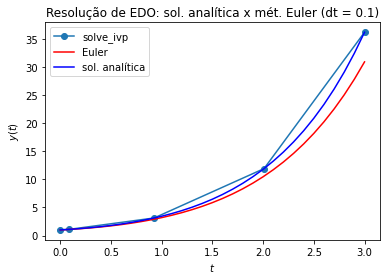
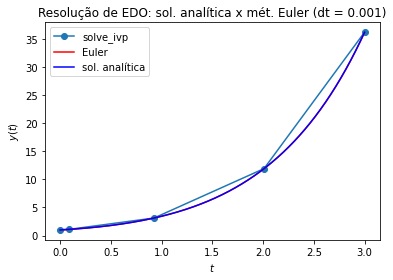
Exemplo: Resolver numericamente o PVI
para \(h=1.0,0.1,0.001\).
Compare a solução numérica com a analítica: \(y_{an}(t) = 2e^{t} - t - 1\).
f = lambda t,y: y + t
yan = lambda t: 2*np.exp(t) - t - 1
y0 = 1
a = 0.0
b = 3.0
T = [1.0,0.1,0.001]
for k in T:
t = np.arange(a, b+k, k)
sol = solve_ivp(f, (a,b), [y0])
y2 = t*0
y2[0] = y0
dt = (b-a)/ (len(t)-1)
for i in range(0,len(t)-1):
y2[i+1] = y2[i] + f(t[i],y2[i])*dt
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(sol.t,sol.y[0],'o-',label='solve_ivp')
plt.plot(t,y2,'r',label='Euler')
plt.plot(t,yan(t),'b',label='sol. analítica')
plt.legend()
s = 'Resolução de EDO: sol. analítica x mét. Euler (dt = ' + str(k) + ')'
plt.title(s)
plt.xlabel('$t$')
plt.ylabel('$y(t)$')