Code Session 2: Newton#

O propósito desta Code Session é resolver problemas de determinação de raízes de equações não lineares polinomiais e transcendentais utilizando a função newton do módulo scipy.optimize. Replicaremos alguns problemas da Code Session 1 e faremos algumas adições.

# Importação de módulos
import numpy as np, matplotlib.pyplot as plt, sympy as sy

Determinação de raízes#

newton#

A função newton localiza a raiz de uma função dentro de um intervalo dado usando o método de Newton, sob especificação da primeira derivada. Os argumentos de entrada obrigatórios desta função são:

  1. a função-alvo f (contínua)

  2. a estimativa inicial x0

Os parâmetros opcionais relevantes são:

  • fprime: a derivada da função, quando disponível. Caso ela não seja especificada, o método da secante é usado.

  • fprime2: a segunda derivada da função, quando disponível. Se ela for especificada, o método de Halley é usado.

  • tol: tolerância (padrão: 1.48e-08)

  • maxiter: número máximo de iterações (padrão: 50)

  • disp: mostra erro se algoritmo não convergir (padrão: True)

O argumento de saída é:

  • x: a estimativa para a raiz de f

# Importação de 'newton'
from scipy.optimize import newton

Problema 1#

Encontre a menor raiz positiva (real) de x3−3.23x2−5.54x+9.84=0 pelo método de Newton.

Resolução#

Definimos a função e sua primeira derivada.

# Função primitiva
def f(x): 
    return x**3 - 3.23*x**2 - 5.54*x + 9.84

# 1a. derivada
def df(x):
    return 3*x**2 - 2*3.23*x - 5.54

Realizamos a análise gráfica.

# Análise gráfica 
x = np.linspace(-4,5)
plt.plot(x,f(x))
plt.plot(x,df(x))
plt.axhline(y=0,color='k',ls='--')
plt.legend(['$f(x)$','$f\'(x)$','$y=0$'],
           loc='lower right');
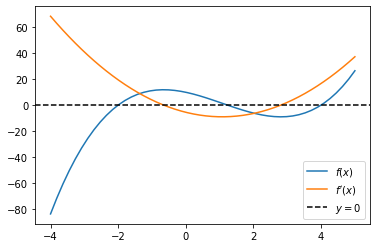
../_images/codeSession-2-newton_11_0.png

Vamos realizar um estudo de diferentes estimativas iniciais e ver o que acontece.

Estimativa inicial: x0=−1#
x0 = -1.
x = newton(f,x0,df) # raiz 
print('Raiz: x = %f' % x)

Raiz: x = -2.000000
Estimativa inicial: x0=0#
x0 = 0.
x = newton(f,x0,df) # raiz 
print('Raiz: x = %f' % x)

Raiz: x = 1.230000
Estimativa inicial: x0=3#
x0 = 3.
x = newton(f,x0,df) # raiz 
print('Raiz: x = %f' % x)

Raiz: x = 4.000000

Problema 2#

Determine a menor raiz não nula positiva de cosh⁡(x)cos⁡(x)−1=0 dentro do intervalo (4,5).

Resolução:#

Primeiramente, vamos escrever a função f(x).

# Função (anônima)
f = lambda x: np.cosh(x)*np.cos(x) - 1

Para computar a primeira derivada, utilizaremos computação simbólica. Veja no início deste notebook que inserimos a instrução a seguir para chamar objetos do módulo sympy.

import sympy as sy

Em primeiro lugar, devemos estabelecer uma variável simbólica xs.

# Variável simbólica
xs = sy.Symbol('x')

Em seguida, devemos utilizar as funções cosh e cos simbólicas para derivar f. Elas serão chamadas de dentro do módulo sympy.

Escrevemos a expressão simbólica para a derivada.

d = sy.diff(sy.cosh(xs)*sy.cos(xs) - 1)
d
−sin⁡(x)cosh⁡(x)+cos⁡(x)sinh⁡(x)

Note que d é um objeto do módulo sympy

type(d)

sympy.core.add.Add

Podemos agora aproveitar a expressão de d para criar nossa derivada. Se imprimirmos d, teremos:

print(d)

-sin(x)*cosh(x) + cos(x)*sinh(x)

Porém, precisamos indicar que as funções serão objetos numpy. Logo, adicionamos np, de modo que:

df = lambda x: - np.sin(x)*np.cosh(x) + np.cos(x)*np.sinh(x)

Agora, realizamos a análise gráfica.

# analise gráfica 
x = np.linspace(4,5)
plt.plot(x,f(x));
plt.plot(x,df(x));
plt.axhline(y=0,color='r',ls='--');
plt.legend(['$f(x)$','$f\'(x)$','$y=0$']);
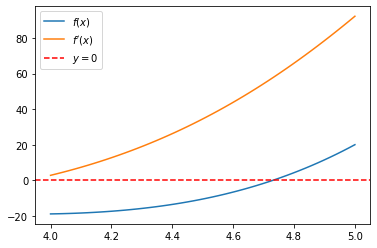
../_images/codeSession-2-newton_34_0.png

Agora, vamos resolver optando pela estimativa inicial x0=4.9.

# resolução com newton 
x0 = 4.9
x = newton(f,x0,df) # raiz 
print('Raiz: x = %f' % x)

Raiz: x = 4.730041

Tarefas#

  1. Reproduza os Problemas de 3 a 8 da Code Session 1 resolvendo com o método newton.

  2. Para os casos possíveis, determine a derivada. Caso contrário, utilize como método da Secante.

  3. Pesquise sobre o método de Halley e aplique-o aos problemas usando a função newton, mas avaliando-a também com a segunda derivada.