Questionário 61 (Q61)¶
Orientações:
Registre suas respostas no questionário de mesmo nome no SIGAA.
O tempo de registro das respostas no questionário será de 10 minutos. Portanto, resolva primeiro as questões e depois registre-as.
Haverá apenas 1 (uma) tentativa de resposta.
Submeta seu arquivo-fonte (utilizado para resolver as questões) em formato .ipynb pelo SIGAA anexando-o à Tarefa denominada “Envio de arquivo” correspondente ao questionário.
Nota: o arquivo-fonte será utilizado apenas como prova de execução da tarefa. Nenhuma avaliação será feita quanto ao estilo de programação.
Questão 1. Observe os gráficos abaixo e julgue os itens a seguir.
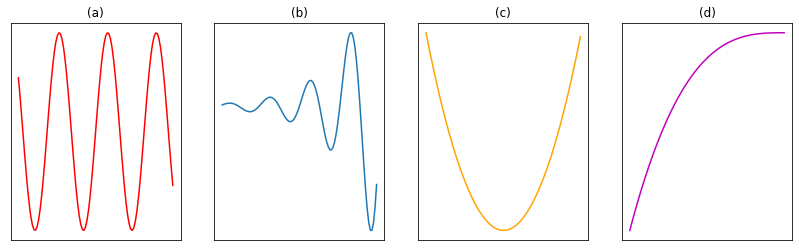
i) existe uma função convexa entre as quatro plotadas.
ii) uma entre as funções plotadas possui convexidade parcial.
iii) duas entre as funções plotadas não são convexas.
Assinale a alternativa correta:
A. São corretos i) e ii), apenas.
B. Apenas i) é correto.
C. São corretos i) e iii), apenas.
D. n.d.a.
Questão 2. A função a seguir simula a curva do potencial de ação de uma membrana:
Use computação simbólica para calcular uma aproximação para \(P'(x=0)\) e assinale a alternativa correta.
A. -67.62
B. 0.25
C. 11.33
D. 0.00
Nota: Use sympy.subs(x,x0).
Questão 3. Considere a função
definida no domínio \([-0.5,-0.1]\). Assinale a alternativa correta:
A. \(f(x)\) não é convexa e \(f'(x) = -\frac{e^{x}}{\text{sen}{\left(6 x \right)}} + \frac{6 e^{- x} \cos{\left(6 x \right)}}{\text{sen}^{2}{\left(6 x \right)}}\)
B. \(f(x)\) é convexa e \(f'(x) = \frac{e^{- x}}{\text{sen}{\left(6 x \right)}} + \frac{6 e^{- x} \cos{\left(6 x \right)}}{\text{sen}^{2}{\left(6 x \right)}}\)
C. \(f(x)\) não é convexa e \(f'(x) = \frac{e^{x}}{\text{sen}{\left(6 x \right)}} + \frac{6 e^{- x} \cos{\left(6 x \right)}}{\text{sen}^{2}{\left(6 x \right)}}\)
D. \(f(x)\) é convexa e \(f'(x) = -\frac{e^{- x}}{\text{sen}{\left(6 x \right)}} + \frac{6 e^{- x} \cos{\left(6 x \right)}}{\text{sen}^{2}{\left(6 x \right)}}\)
