Correlação¶
Correlação é qualquer associação estatística entre um par de variáveis. Quanto mais correlacionadas estão duas variáveis, mais “alinhamento” há entre elas. Isto é, uma análise de correlação fornece um número que resume o grau de relacionamento linear entre duas variáveis. Introduziremos este assunto com alguns conceitos fundamentais.
Associação entre variáveis e causalidade¶
A associação entre duas variáveis pode ocorrer de duas formas:
correlacional: neste caso, não há interferência alguma sobre as variáveis observadas. As variáveis são aleatórias e seus comportamentos ocorrem conforme a “natureza” determina. Por exemplo, o exercício físico e a queima calórica possuem correlação positiva, pois quanto mais intensamente nos exercitamos, mais queimamos caloria.
experimental: neste caso, uma das variáveis é controlada e esta interfere sobre a outra. Isto é, uma variável A é a causa (variável independente) e a outra, B, o efeito (variável independente). Uma sentença lógica do tipo “se A, então B” estabelece a idéia de causalidade. Por exemplo: quando cientistas estudam a administração de fármacos em um organismo, eles analisam os efeitos dessa droga naquele organismo. Logo, a droga é a causa; a resposta orgânica, o efeito.
A causalidade é um assunto muito mais delicado e possui fortes implicações filosóficas, pois, em geral, para se concluir que B é consequência de A, é necessário ter uma prova disso. Porém, nem sempre é possível provar muitas relações de causa/efeito que presenciamos. Para uma discussão no âmbito filosófico, consulte este post.
Correlação e dependência linear¶
Podemos interpretar a correlação também pelo ponto de vista de “dependência linear”. Duas variáveis perfeitamente correlacionadas são similares a dois vetores paralelos, ou seja, linearmente dependentes. Por outro lado, duas variáveis totalmente não correlacionadas são similares a dois vetores perpendiculares, ou seja, linearmente independentes.
Escore padronizado¶
Medir correlações envolve desafios. Um deles surge quando as variáveis que queremos comparar não estão expressas na mesma unidade. Por exemplo, você pode desejar correlacionar alturas medidas em centímetros e pesos medidos em quilogramas. Por outro lado, ainda que as unidades sejam as mesmas, o segundo desafio aparece quando as variáveis provêm de distribuições diferentes.
As duas soluções comuns para lidar com esses problemas são:
Transformar todos os valores para um escore padronizado.
Transformar todos os valores para ranques baseados em percentis.
Como veremos adiante, a primeira solução leva-nos ao coeficiente de correlação de Pearson; a segunda, ao coeficiente de Spearman.
Note
Outros nomes para o escore padronizado são escore Z, teste Z ou Z-score.
Para converter uma série \(X\) de valores \(x_i\) em uma escala padronizada de escores, subtraímos a média dos dados e dividimos esta diferença pelo desvio padrão. Isto é:
onde \(\mu\) é a média e \(\sigma\) o desvio padrão.
Ao dividir os desvios (numerador) pelo desvio padrão, na verdade, estamos normalizando o desvio, de modo que os valores \(z_i\) da nova série \(Z\) são adimensionais (não possuem unidades), possuam média 0 e variância 1. A série \(Z\) herda a “forma” de \(X\).
Primeiro, importemos os módulos que usaremos.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sts
Vejamos exemplos:
# dataframe
dfp = pd.DataFrame({'Idade': np.array([20,19,21,22,20]),
'Peso': np.array([55,80,62,67,73]),
'Altura': np.array([162,178,162,165,171]),
'IMC':np.array([20.96, 25.25, 23.62, 24.61, 24.96])},
index=['Ana','João','Maria','Pedro','Túlio'])
dfp
| Idade | Peso | Altura | IMC | |
|---|---|---|---|---|
| Ana | 20 | 55 | 162 | 20.96 |
| João | 19 | 80 | 178 | 25.25 |
| Maria | 21 | 62 | 162 | 23.62 |
| Pedro | 22 | 67 | 165 | 24.61 |
| Túlio | 20 | 73 | 171 | 24.96 |
Vamos calcular o z-score para todas as Series do DataFrame.
def zScore(df,colname):
s = df[colname]
return (s - s.mean())/s.std(ddof=0) # ddof = 0 para dividir por N
# cria novo dataframe de z-scores
Z = {}
for c in dfp.columns:
Z[c + ':Z-score'] = zScore(dfp,c)
dfpz = pd.DataFrame(Z)
dfpz
| Idade:Z-score | Peso:Z-score | Altura:Z-score | IMC:Z-score | |
|---|---|---|---|---|
| Ana | -0.392232 | -1.435277 | -0.910359 | -1.871626 |
| João | -1.372813 | 1.458427 | 1.690666 | 0.878126 |
| Maria | 0.588348 | -0.625040 | -0.910359 | -0.166652 |
| Pedro | 1.568929 | -0.046299 | -0.422666 | 0.467906 |
| Túlio | -0.392232 | 0.648190 | 0.552718 | 0.692245 |
Comentários:
Os z-score ajudam a entender se uma observação específica é comum ou excepcional:
z-score < 0 representam valores abaixo da média;
z-score > 0 representam valores acima da média;
z-score da média é 0, uma vez que ela é ponto médio;
A soma dos z-score = 0;
z-scores com valores positivos extremamente altos indicam uma distribuição com assimetria à direita (mais sobre isso adiante);
z-scores com valores negativos extremamente altos indicam uma distribuição com assimetria à esquerda (mais sobre isso adiante);
se |z-score| > 2, a distribuição é incomum ou excepcional.
# Z-Score das séries têm soma nula
dfpz.sum(axis=0)
Idade:Z-score 6.772360e-15
Peso:Z-score -3.219647e-15
Altura:Z-score 4.662937e-15
IMC:Z-score -6.994405e-15
dtype: float64
Calculando o z-score por função predefinida.
Z2 = {}
for c in dfp.columns:
Z2[c + ':Z-score'] = sts.zscore(dfp[c])
dfpz2 = pd.DataFrame(Z2,index=dfp.index)
dfpz2
| Idade:Z-score | Peso:Z-score | Altura:Z-score | IMC:Z-score | |
|---|---|---|---|---|
| Ana | -0.392232 | -1.435277 | -0.910359 | -1.871626 |
| João | -1.372813 | 1.458427 | 1.690666 | 0.878126 |
| Maria | 0.588348 | -0.625040 | -0.910359 | -0.166652 |
| Pedro | 1.568929 | -0.046299 | -0.422666 | 0.467906 |
| Túlio | -0.392232 | 0.648190 | 0.552718 | 0.692245 |
# ambos os métodos dão resultados idênticos
(dfpz == dfpz2).all()
Idade:Z-score True
Peso:Z-score True
Altura:Z-score True
IMC:Z-score True
dtype: bool
Plot de z-scores¶
A plotagem dos z-scores pode ser feita diretamente com plot a partir da Series \(Z\) de interesse.
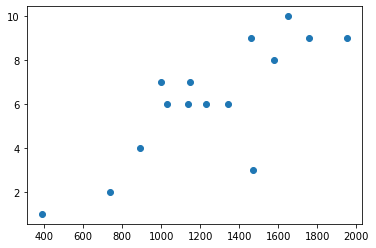
dfpz['Peso:Z-score'].plot(marker='o',ls='');
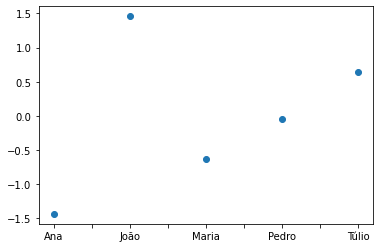
dfpz['IMC:Z-score'].plot(marker='o',ls='',color='g');

Comentários:
A partir desses plots, vemos claramente qual discente está “acima da”, “abaixo da” ou “na” média perante a variável escolhida.
Covariância¶
Já vimos que a variância de um conjunto de dados mede quanto uma variável desvia-se do valor médio, seja em nível de amostra ou de população. Quando queremos compreender como duas variáveis variam juntas, aplicamos o conceito de covariância. Se \(X\) e \(Y\) são duas Series, a covariância entre ambas é dada por
onde \(n\) é o número de elementos na série (igual em ambas) e \(\mu_X\) (\(\mu_Y\)) é a média de \(X\)(\(Y\)).
Notemos que a covariância é uma “média” do produto dos desvios.
Exemplo: vamos criar uma função para o cálculo da variância.
# covariância
def cov(df,colname1,colname2):
s1,s2 = df[colname1],df[colname2]
return np.dot( s1 - s1.mean(), s2 - s2.mean() )/(len(s1)-1)
Testemos a covariância entre as variáveis de nosso DataFrame de estudo.
cov(dfp,'Altura','Peso'), cov(dfp,'Idade','Peso'), cov(dfp,'Idade','Altura')
(62.7, -4.7, -5.300000000000001)
Comentários:
Esses cálculos mostram que variações de altura e peso interferem consideravelmente uma na outra “na mesma direção”.
Porém, não notamos o mesmo comportamento para idade e peso ou para idade e altura.
Podemos checar o cálculo de nossa função com a função var do pandas, sabendo que \(\text{cov}(X,X) = \text{var}(X) = S^2(X), \, \forall X\).
cov(dfp,'Altura','Altura'), dfp['Altura'].var()
(47.3, 47.3)
Outra forma de calcular a covariância é usar o método cov de uma pandas.Series.
dfp['Altura'].cov(dfp['Peso'])
62.7
Matriz de covariâncias¶
Podemos usar a função numpy.cov() para computar a covariância entre duas Series \(X\) e \(Y\). Para tanto, devemos passar a matriz \([X \ \ Y]\) como parâmetro para a função.
A resposta é uma matriz de covariâncias 2x2 cujas entradas são:
X, Y = dfp['Altura'], dfp['Peso']
np.cov(np.array([X,Y]))
array([[47.3, 62.7],
[62.7, 93.3]])
Correlação¶
Uma das dificuldades conhecidas da covariância é a sua interpretação. Uma vez que ela é dada pelo produto das unidades de suas entradas, muito frequentemente será inviável atribuir significado ao número. Por exemplo, se a unidade de \(X\) for quilogramas e \(Y\) for anos, a unidade da covariância seria quilogramas vezes anos. Um meio de solucionar este problema é dividir o produto da covariância pelo desvio padrão de cada série de dados, assim formando o conceito de correlação, dado por:
Em outras palavras, a correlação é a soma do produto de escores padronizados.
Coeficiente de correlação de Pearson¶
Se os desvios forem retirados da somatória, a expressão torna-se:
O número \(\rho\) é chamado de coeficiente de correlação de Pearson, ou simplesmente correlação de Pearson, e vale que \(-1 \leq \rho \leq 1\). A magnitude de \(\rho\) determina a força de correlação entre as variáveis. Em geral, a seguinte interpretação é utilizada:
\(\rho = 1\): as variáveis são perfeitamente correlacionadas.
\(\rho = 0\): as variáveis são correlacionadas de alguma forma, mas não linearmente. Neste sentido, \(\rho\) subestimará a força da dependência linear.
\(\rho = -1\): idem, porém negativamente.
Na finalidade de predizer algo nos dados, correlação máxima negativa, assim como positva, podem ser igualmente boas. No mundo real, correlações perfeitas são raridade, mas estimativas “quase” perfeitas podem ser feitas.
A Fig. 9 mostra datasets que possuem correlação linear e não-linear, acompanhados dos valores de \(\rho\). Como se observa na linha superior, \(\rho = \pm 1\) mostram plotagens de retas com inclinação positiva ou negativa, ao passo que valores intermediários mostram “manchas” que variam de formas elípticas inclinadas à esquerda ou à direita e circular. Na linha inferior, vemos diversos casos em que \(\rho=0\), mas “manchas” com estruturas “não lineares” bem definidas são distinguíveis.
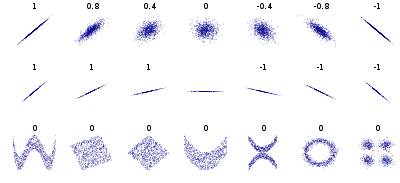
Fig. 9 Datasets com diferentes correlações de Pearson. Fonte: Wikipedia.¶
Exemplo: A tabela a seguir contém dados coletados na administração de um zoológico para alguns dias do mês de abril de 2021. Nesta ordem, a tabela mostra o número de visitantes no zoológico, o número de tickets de estacionamento adquiridos e a temperatura média contabilizados por dia.
Visitantes |
Tickets |
Temperatura |
|---|---|---|
1580 |
8 |
35 |
1230 |
6 |
38 |
1950 |
9 |
32 |
890 |
4 |
26 |
1140 |
6 |
31 |
1760 |
9 |
36 |
1650 |
10 |
38 |
1470 |
3 |
30 |
390 |
1 |
21 |
1460 |
9 |
34 |
1000 |
7 |
36 |
1030 |
6 |
32 |
740 |
2 |
25 |
1340 |
6 |
37 |
1150 |
7 |
34 |
O arquivo com os dados está disponível aqui. Vamos buscar correlações nos dados.
Carregando o arquivo:
zoo = pd.read_csv('../database/visitantes-zoo.csv'); zoo
| Visitantes | Tickets:Parking | Temperatura (C) | |
|---|---|---|---|
| 0 | 1580.0 | 8.0 | 35.0 |
| 1 | 1230.0 | 6.0 | 38.0 |
| 2 | 1950.0 | 9.0 | 32.0 |
| 3 | 890.0 | 4.0 | 26.0 |
| 4 | 1140.0 | 6.0 | 31.0 |
| 5 | 1760.0 | 9.0 | 36.0 |
| 6 | 1650.0 | 10.0 | 38.0 |
| 7 | 1470.0 | 3.0 | 30.0 |
| 8 | 390.0 | 1.0 | 21.0 |
| 9 | 1460.0 | 9.0 | 34.0 |
| 10 | 1000.0 | 7.0 | 36.0 |
| 11 | 1030.0 | 6.0 | 32.0 |
| 12 | 740.0 | 2.0 | 25.0 |
| 13 | 1340.0 | 6.0 | 37.0 |
| 14 | 1150.0 | 7.0 | 34.0 |
Para calcular a correlação de Pearson entre duas séries, podemos usar a função pearsonr() do módulo scipy.stats.
Note
O segundo argumento de pearsonr() é o valor p.
corr1,_ = sts.pearsonr(zoo['Visitantes'],zoo['Tickets:Parking']);
corr2,_ = sts.pearsonr(zoo['Visitantes'],zoo['Temperatura (C)']);
corr1,corr2
(0.8044243219605788, 0.6815723802241447)
Comentários:
O coeficiente de Pearson mostra que há uma “força” de correlação não desprezível entre o número de visitantes e tickets vendidos.
Esta correlação é menor para a faixa de temperaturas médias.
A correlação pode também ser calculada através do método corr de uma Series do pandas.
zoo['Visitantes'].corr(zoo['Tickets:Parking'])
0.8044243219605786
zoo['Visitantes'].corr(zoo['Temperatura (C)'])
0.6815723802241447
Correlações pareadas¶
Usando o método pandas.DataFrame.corrwith() é possível calcular correlações pareadas entre colunas de um DataFrame ou linhas de outra Series ou DataFrame.
No exemplo abaixo, passamos uma Series como argumento. A resposta são os mesmos valores obtidos anteriormente, porém na forma de uma Series. O valor unitário é devido à correlação da variável com ela própria.
zoo.corrwith(zoo['Visitantes'])
Visitantes 1.000000
Tickets:Parking 0.804424
Temperatura (C) 0.681572
dtype: float64
Gráfico de dispersão¶
Antes de calcular cegamente o valor de \(\rho\) para séries de dados, é interessante fazer um gráfico de dispersão (scatter plot) entre as variáveis. Podemos fazer isto com o matplotlib.pyplot.plot() e tipo de marcador o ou com matplotlib.pyplot.scatter().
fig,ax = plt.subplots(1,2,figsize=(10,3))
# plot 1
ax[0].plot(zoo['Visitantes'],zoo['Tickets:Parking'],'o',label=f'corr={round(corr1,2)}')
ax[0].set_xlabel('No. visitantes');
ax[0].set_ylabel('Tickets de estacionamento');
ax[0].legend()
# plot 2
ax[1].plot(zoo['Visitantes'],zoo['Temperatura (C)'],'or',label=f'corr={round(corr2,2)}')
ax[1].set_xlabel('No. visitantes');
ax[1].set_ylabel('Temperatura (C)');
ax[1].legend();
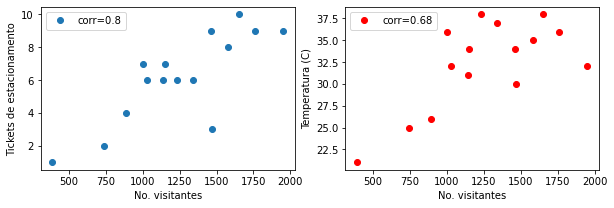
Reproduzindo com plt.scatter:
plt.scatter(zoo['Visitantes'],zoo['Tickets:Parking']);