Análise de redes complexas¶
Rede (network) é uma forma de organizar e representar dados discretos. Elas diferem da forma tabular, em que linhas e colunas são as estruturas fundamentais, e funcionam com base em dois conceitos:
entidades, ou atores, ou ainda nós, e
relacionamentos, ou links, ou arcos, ou ainda, conexões.
Casualmente, o conceito de rede se confunde com o conceito matemático de grafo, para o qual as entidades são chamadas vértices e os relacionamentos arestas. Usa-se a notação \(G(V,E)\) para designar um grafo genérico \(G\) com um conjunto \(V\) de vértices e um conjunto \(E\) de arestas. A Fig. Fig. 12 esboça um grafo genérico.
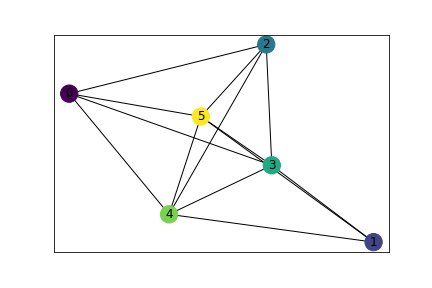
Fig. 12 Grafo genérico contendo 6 vértices e 13 arestas.¶
Aplicações¶
Com o barateamento dos recursos de computação no final do século XX, a análise de redes complexas (do inglês complex network analysis, ou CNA) evoluiu como uma área de pesquisa independente. Desde então, tornou-se possível mapear bancos de dados enormes e extrair conhecimento a partir de um emaranhado complexo de interligações.
No século XXI, percebemos um interesse explosivo em CNA. Algumas aplicações modernas incluem, mas não se limitam a:
transporte, para planejamento de malhas ferroviárias, rodovias e conexões entre cidades;
sociologia, para entender pessoas, seu comportamento, interação em redes sociais, orientações de pensamento e preferências;
energia, para sistematizar linhas de transmissão de energia elétrica;
biologia, para modelar redes de transmissão de doenças infecciosas;
ciência, para encontrar os núcleos de pesquisa mais influentes do mundo em um determinado campo do conhecimento.
O módulo networkx¶
Neste capítulo, introduziremos alguns conceitos relacionados à CNA, tais como componentes conexas, medidades de centralidade e visualização de grafos usando o módulo Python networkx. Este módulo tornou-se popular pela sua versatilidade. Alguns de seus pontos positivos são:
facilidade de instalação;
ampla documentação no site oficial;
extenso conjunto de funções e algoritmos;
versatilidade para lidar com redes de até 100.000 nós.
Note
Algumas ferramentas com potencial similar ao networkx são igraph e graph-tool. Especificamente para visualização, você poderá se interessar pelo Graphviz ou pelo Gephi.
Vamos praticar um pouco com este módulo para entender conceitos fundamentais. Em seguida, faremos uma aplicação. Supondo que você já tenha instalado o networkx, importe-o:
import networkx as nx
Criação de grafos não dirigidos¶
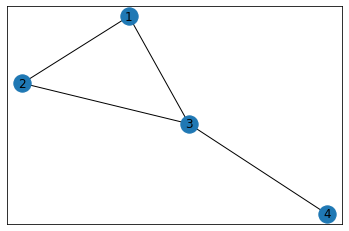
Em seguida vamos criar um grafo \(G\) não dirigido. Isso significa que o sentido da aresta é irrelevante. Contudo, vale comentar que há situações em que o sentido da aresta importa. Neste caso, diz-se que o grafo é dirigido.
# cria grafo não dirigido com 4 vértices
# inicializa
G = nx.Graph()
# adiciona arestas explicitamente
G.add_edge(1,2)
G.add_edge(1,3)
G.add_edge(2,3)
G.add_edge(3,4)
Em seguida, visualizamos o grafo com draw_networkx.
nx.draw_networkx(G)
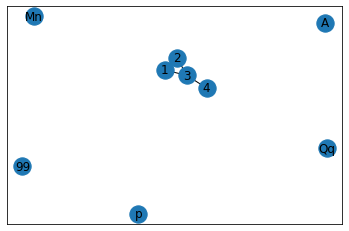
Adição e deleção de nós e arestas¶
Podemos adicionar nós indvidualmente ou por meio de uma lista, bem como usar strings como nome.
G.add_node('A')
G.add_nodes_from(['p',99,'Qq'])
G.add_node('Mn') # nó adicionado por engano
nx.draw_networkx(G)
Podemos fazer o mesmo com arestas sobre nós existentes ou não existentes.
G.add_edge('A','p') # aresta individual
G.add_edges_from([(1,99),(4,'A')]) # aresta por lista (origem, destino)
G.add_edge('Mn','no') # 'no' não existente
nx.draw_networkx(G)
Nós e arestas podem ser removidos de maneira similar.
G.remove_node('no')
G.remove_nodes_from(['Qq',99,'p'])
nx.draw_networkx(G)
G.remove_edge(1,2)
G.remove_edges_from([('A',4),(1,3)])
nx.draw_networkx(G)
Para remover todas os nós e arestas do grafo, mas mantê-lo criado, usamos clear.
G.clear()
Verificamos que não há nós nem arestas:
len(G.nodes()), len(G.edges)
(0, 0)
Para deletá-lo completamente, podemos fazer:
del G
Criação de grafos aleatórios¶
Podemos criar um grafo aleatório de diversas formas. Com random_geometric_graph, o grafo de n nós uniformemente aleatórios fica restrito ao “cubo” unitário de dimensão dim e conecta quaisquer dois nós u e v cuja distância entre eles é no máximo raio.
# 30 nós com raio de conexão 0.2
n = 30
raio = 0.2
G = nx.random_geometric_graph(n,raio,dim=2)
nx.draw_networkx(G)
# 30 nós com raio de conexão 5
n = 30
raio = 5
G = nx.random_geometric_graph(n,raio,dim=2)
nx.draw_networkx(G)
# 12 nós com raio de conexão 1.15
n = 12
raio = 1.15
G = nx.random_geometric_graph(n,raio,dim=2)
nx.draw_networkx(G)
# 12 nós com raio de conexão 0.4
n = 12
raio = 0.4
G = nx.random_geometric_graph(n,raio,dim=2)
nx.draw_networkx(G)
Impressão de listas de nós e de arestas¶
Podemos acessar a lista de nós ou de arestas com:
G.nodes()
NodeView((0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11))
G.edges()
EdgeView([(0, 5), (0, 11), (1, 3), (1, 2), (1, 5), (1, 4), (1, 7), (2, 4), (3, 4), (3, 7), (3, 9), (3, 5), (3, 11), (3, 8), (4, 5), (4, 11), (4, 7), (5, 7), (5, 11), (5, 8), (6, 11), (6, 8), (6, 10), (6, 9), (7, 9), (7, 11), (7, 8), (8, 9), (8, 11), (9, 11), (10, 11)])
Notemos que as arestas são descritas por meio de tuplas (origem,destino).
Se especificarmos data=True, atributos adicionais são impressos. Para os nós, vemos pos como a posição espacial.
print(G.nodes(data=True))
[(0, {'pos': [0.14016708535353195, 0.6030612677990583]}), (1, {'pos': [0.7551166126779706, 0.5753984722722648]}), (2, {'pos': [0.587815560861345, 0.9262306002179045]}), (3, {'pos': [0.6481883004357897, 0.23944971393177616]}), (4, {'pos': [0.5407112650886972, 0.5928863158800595]}), (5, {'pos': [0.36356802456758663, 0.5063407090207792]}), (6, {'pos': [0.13333289318770103, 0.10093555742924487]}), (7, {'pos': [0.5880577194412443, 0.4328559322005747]}), (8, {'pos': [0.4877270706931097, 0.16480065213848483]}), (9, {'pos': [0.4864756110584624, 0.06055043228282264]}), (10, {'pos': [0.06553095561423039, 0.20127799578298156]}), (11, {'pos': [0.2821978870896149, 0.3551844724031613]})]
No caso das arestas, nenhum atributo existe para este grafo. Contudo, em grafos mais complexos, é comum ter capacidade e peso como atributos. Ambas são relevantes em estudos de fluxo, em que se associa a arestas uma “capacidade” de transporte e um “peso” de relevância.
print(G.edges(data=True))
[(0, 5, {}), (0, 11, {}), (1, 3, {}), (1, 2, {}), (1, 5, {}), (1, 4, {}), (1, 7, {}), (2, 4, {}), (3, 4, {}), (3, 7, {}), (3, 9, {}), (3, 5, {}), (3, 11, {}), (3, 8, {}), (4, 5, {}), (4, 11, {}), (4, 7, {}), (5, 7, {}), (5, 11, {}), (5, 8, {}), (6, 11, {}), (6, 8, {}), (6, 10, {}), (6, 9, {}), (7, 9, {}), (7, 11, {}), (7, 8, {}), (8, 9, {}), (8, 11, {}), (9, 11, {}), (10, 11, {})]
Criação de redes a partir de arquivos¶
Um modo conveniente de criar redes é ler diretamente um arquivo contendo informações sobre a conectividade. O dataset que usaremos a partir deste ponto em diante corresponde a uma rede representando a amizade entre usuários reais do Facebook. Cada usuário é representado por um vértice e um vínculo de amizade por uma aresta. Os dados são anônimos.
Carregamos o arquivo .txt com networkx.read_edgelist.
fb = nx.read_edgelist('../database/fb_data.txt')
len(fb.nodes), len(fb.edges)
(4039, 88234)
Vemos que esta rede possui 4039 usuários e 88234 vínculos de amizade. Você pode plotar o grafo para visualizá-lo, porém pode demorar um pouco…
Propriedades relevantes¶
Vejamos algumas propriedades de interesse de redes e grafos.
Grau¶
O grau de um nó é o número de arestas conectadas a ele. Assim, o grau médio da rede do Facebook acima pode ser calculado por:
fb.number_of_edges()/fb.number_of_nodes()
21.84550631344392
ou
fb.size()/fb.order()
21.84550631344392
Ambos os resultados mostram que cada usuário nesta rede tem pelo menos 21 amizades.
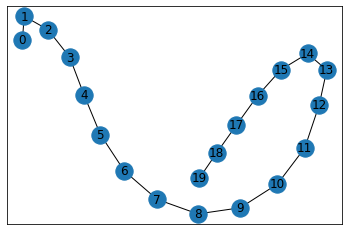
Caminho¶
Caminho é uma sequencia de nós conectados por arestas contiguamente. O caminho mais curto em uma rede é o menor número de arestas a serem visitadas partindo de um nó de origem u até um nó de destino v.
A seguir, plotamos um caminho formado por 20 nós.
Gpath = nx.path_graph(20)
nx.draw_networkx(Gpath)
Componente¶
Um grafo é conexo se para todo par de nós, existe um caminho entre eles. Uma componente conexa, ou simplesmente componente de um grafo é um subconjunto de seus nós tal que cada nó no subconjunto tem um caminho para todos os outros.
Podemos encontrar todas as componentes da rede do Facebook usando connected_componentes. Entretanto, o resultado final é um objeto generator. Para acessarmos as componentes, devemos usar um iterador.
cc = nx.connected_components(fb)
# varre componentes e imprime os primeiros 5 nós
for c in cc:
print(list(c)[0:5])
['572', '3423', '3794', '1409', '1318']
Uma vez que há apenas uma lista impressa, temos que a rede do Facebook, na verdade, é uma componente única. De outra forma,
# há apenas 1 componente conexa, a própria rede
nx.number_connected_components(fb)
1
Subgrafo¶
Subgrafo é um subconjunto dos nós de um grafo e todas as arestas que os conectam. Para selecionarmos um subgrafo da rede Facebook, usamos subgraph. Os argumentos necessários são: o grafo original e uma lista dos nós de interesse. Abaixo, geramos uma lista aleatória de ng nós.
from numpy.random import randint
# número de nós do subgrafo
ng = 40
# identifica nós (nomes são strings)
nodes_to_get = randint(1,fb.number_of_nodes(),ng).astype(str)
# extrai subgrafo
fb_sub = nx.subgraph(fb,nodes_to_get)
# plota
nx.draw_networkx(fb_sub)
Se fizermos alguma alteração no grafo original, pode ser que o número de componentes se altere. Vejamos:
# copia grafo
fb_less = fb.copy()
# remove o nó '0'
fb_less.remove_node('0')
# novas componentes
nx.number_connected_components(fb_less)
19
Neste exemplo, a retirada de apenas um nó do grafo original resultou em 19 componentes, com número variável de elementos.
ncs = []
for c in nx.connected_components(fb_less):
ncs.append(len(c))
# número de componentes em ordem
sorted(ncs,reverse=True)
[4015, 3, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Métricas de centralidade¶
A centralidade de um nó mede a sua importância relativa no grafo. Em outras palavras, nós mais “centrais” tendem a ser considerados os mais influentes, privilegiados ou comunicativos.
Em uma rede social, por exemplo, um usuário com alta centralidade pode ser um influencer, um político, uma celebridade, ou até mesmo um malfeitor. Há diversas métricas de centralidade disponíveis. Aqui veremos as 4 mais corriqueiras:
centralidade de grau (degree centrality): definida pelo número de arestas de um nó;
centralidade de intermediação(betweeness centrality): definida pelo número de vezes em que o nó é visitado ao tomarmos o caminho mais curto entre um par de nós distintos deste. Esta centralidade pode ser imaginada como uma “ponte” ou “pedágio”.
centralidade de proximidade (closeness centrality): definida pelo inverso da soma das distâncias do nó de interesse a todos os outros do grafo. Ela quão “próximo” o nó é de todos os demais. Um nó com alta centralidade é aquele que, grosso modo, “dista por igual” dos demais.
centralidade de autovetor (eigenvector centrality): definida pelo escore relativo para um nó tomando por base suas conexões. Conexões com nós de alta centralidade aumentam seu escore, ao passo que conexões com nós de baixa centralidade reduzem seu escore. De certa forma, ela mede como um nó está conectado a nós influentes.
Em particular, um nó com alta centralidade de proximidade e alta centralidade de intermediação é chamado de hub.
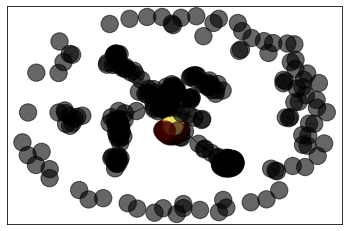
Vamos calcular as centralidades de um subgrafo da rede do Facebook. Primeiro, extraímos um subgrafo menor.
# número de nós do subgrafo
ng = 400
# identifica nós (nomes são strings)
nodes_to_get = randint(1,fb.number_of_nodes(),ng).astype(str)
# extrai subgrafo
fb_sub_c = nx.subgraph(fb,nodes_to_get)
import matplotlib.pyplot as plt
# centralidade de grau
deg = nx.degree_centrality(fb_sub_c)
nx.draw_networkx(fb_sub_c,
with_labels=False,
node_color=list(deg.values()),
alpha=0.6,
cmap=plt.cm.afmhot)

# centralidade de intermediação
bet = nx.betweenness_centrality(fb_sub_c)
nx.draw_networkx(fb_sub_c,
with_labels=False,
node_color=list(bet.values()),
alpha=0.6,
cmap=plt.cm.afmhot)

# centralidade de proximidade
cln = nx.closeness_centrality(fb_sub_c)
nx.draw_networkx(fb_sub_c,
with_labels=False,
node_color=list(cln.values()),
alpha=0.6,
cmap=plt.cm.afmhot)

# centralidade de autovetor
eig = nx.eigenvector_centrality(fb_sub_c)
nx.draw_networkx(fb_sub_c,
with_labels=False,
node_color=list(eig.values()),
alpha=0.6,
cmap=plt.cm.afmhot)
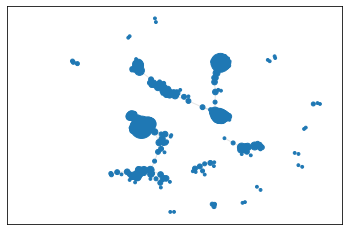
Layouts de visualização¶
Podemos melhorar a visualização das redes alterando os layouts. O exemplo a seguir dispõe o grafo em um layout melhor, chamado de spring. Este layout acomoda a posição dos nós iterativamente por meio de um algoritmo especial. Além disso, a centralidade de grau está normalizada no intervalo [0,1] e escalonada.
Com o novo plot, é possível distinguir “comunidades”, sendo os maiores nós os mais centrais.
from numpy import array
pos_fb = nx.spring_layout(fb_sub_c,iterations = 50)
nsize = array([v for v in deg.values()])
nsize = 500*(nsize - min(nsize))/(max(nsize) - min(nsize))
nodes = nx.draw_networkx_nodes(fb_sub_c, pos = pos_fb, node_size = nsize)
edges = nx.draw_networkx_edges(fb_sub_c, pos = pos_fb, alpha = .1)
Um layout aleatório pode ser plotado da seguinte forma:
pos_fb = nx.random_layout(fb_sub_c)
nx.draw_networkx(fb_sub_c,pos_fb,with_labels=False,alpha=0.5)