Análise de regressão¶
Como vimos no capítulo anterior, a correlação investiga se existe ou não interferência entre duas variáveis. Em particular, ela procura se ambas possuem algum grau de dependência linear. Indo um pouco além, a análise de regressão, ou simplesmente regressão, busca saber de que maneira uma variável pode predizer o comportamento da outra. Assim, no mundo real, algumas perguntas que se quer responder são:
Como o volume de vendas de canetas esferográficas muda se o preço da unidade subir?
De que maneira a taxa de inflação deste ano pode predizer o aumento do aluguel para os próximos dois meses?
A que horas seria melhor sair da universidade para evitar ficar preso pelo tráfego intenso na via?
Perguntas como essas tem uma característica comum. Elas exigem uma resposta que pode ser expressa como uma combinação de uma ou mais variáveis independentes, que são também chamadas de preditores ou covariantes. Assim, o objetivo de uma análise de regressão é construir modelos preditivos a partir dos dados.
Note
A origem do nome regressão deve-se ao estatístico inglês do século XIX Sir Francis Galton. Galton usou o termo para interpretar resultados de um experimento sobre hereditariedade, para o qual coletou alturas de pais e filhos para realizar predições sobre alturas das próximas gerações. Percebendo que a altura de um filho “regredia” (era menor do que) em relação à altura de seus pais por um fator de 2/3, publicou um artigo intitulado Regression towards Mediocrity in Hereditary Stature que, ironicamente, deu surgimento ao nome que usamos para o método estatístico que estamos aprendendo. Galton não aplicou o método dos mínimos quadrados (que é a base teórica para a regressão linear), já conhecido há 80 anos antes de sua época por Gauss e Legendre. Ele simplesmente “traçou uma reta”. Para Galton, a “regressão” representava apenas uma tendência de os dados “reverterem” a tendência média. Isto é, a origem do método regressão é uma “ironia do destino”. Para saber a história completa, veja este post.
Regressão linear¶
O modelo mais básico de regressão é o linear. A regressão linear tenta ajustar um modelo matemático aos dados disponíveis cuja resposta \({\bf y}\) depende linearmente de até \(d\) preditores. Em termos vetoriais, o modelo pode ser descrito como:
em que os \(a_i \in \mathbb{R}, \, i = 1,\ldots d\), são os parâmetros ou coeficientes do modelo e os \({\bf x}_i\) as variáveis.
Se levarmos em conta \(n\) observações de cada variável, cada um dos \({\bf x}_i\) e \({\bf y}\) são todos identificados como vetores do espaço \(\mathbb{R}^n\), de maneira que a equação anterior, reescrita como um sistema matricial, assume a forma \({\bf y} = {\bf X}{\bf a}\), onde
Regressão linear simples¶
A regressão linear simples contém apenas um regressor e o modelo é a equação analítica de uma reta. Escrevemos
onde \(a_0\) é o termo constante, também chamado de offset ou intercept, e \(a_1\) é a inclinação. Logo, dados \(n\) pares de valores \((x_i, y_i)\), para preditor e resposta, respectivamente, determinamos \(a_0\) e \(a_1\) e, enfim, podemos explicar como ambas as variáveis se relacionam.
Entretanto, uma pergunta a se fazer é a seguinte: quais seriam os valores de \(a_0\) e \(a_1\) que produziriam a melhor reta para os dados? Em outras palavras, existe uma reta que explica como \({\bf y}\) depende linearmente de \({\bf x}\) da melhor forma possível? A resposta é sim. Tal reta será aquela que produz os menores erros locais no sentido do método conhecido como mínimos quadrados (least squares).
Mínimos quadrados¶
O método dos mínimos quadrados sugere que a distância Euclidiana entre os valores preditos (modelados) e os valores disponíveis (conhecidos) deve ser minimizada. Na linguagem matemática, devemos encontrar \(a_0\) e \(a_1\) de modo que a norma do resíduo (ou erro) \({\bf r}\) seja o menor possível, isto é, que
seja minimizada. Este problema recai em um problema de otimização e equivale a buscar o ponto de mínimo global \((a_0,a_1)\) de uma função quadrática \(F(x,y)\). Grosso modo, achar \((a_0,a_1)\), tal que.
Você estudará isto futuramente.
Estudo de caso: o gelo marinho e as mudanças climáticas¶
Vamos entender a análise de regressão por meio de um estudo de caso. A pergunta que queremos responder é:
A queda na área coberta por gelo no mar é causada pela alteração do clima?
Vamos trabalhar com o dataset G02135 - Sea Ice Index, Version 3, do NSIDC.
import pandas as pd
import numpy as np
import seaborn as sb
import scipy.stats as sts
import matplotlib.pyplot as plt
sii = pd.read_csv('../database/Sea_Ice_Index_Monthly_Baffin-Area-km^2.csv')
month = 'jan'
s = sb.lmplot(x='year',y=month,data=sii,fit_reg=True);
s.set(title='Ice coverage area in Baffin Area [km2]');
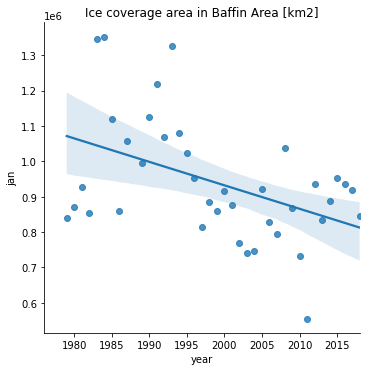
Comentários:
A função
lmplot()realiza a análise de regressão simples com o modelo linear (reta) a partir dos dados passados.O dataset em questão mostra que a área de cobertura do gelo na área de Baffin está sob uma tendência de declínio desde 1980.
A reta da regressão pode ser retirada do gráfico usando
fit_reg=False.
A seguir, “desdobramos” o DataFrame original para realizar uma análise de regressão durante os anos de 1997 a 2017 levando em conta valores mensais.
# intervalo de 20 anos
siif = sii.set_index('year').loc[1997:2017]
# desdobra o DataFrame
siif2 = pd.DataFrame(columns=['year','month','area'])
for i in siif.index:
# astype('float') necessário aqui, pois como 'Int64' temos erro de SVD em lmplot
c1 = pd.Series(np.full(12,i)).astype('float')
c2 = pd.Series(range(1,13)).astype('float')
c3 = siif.loc[i]
d = pd.DataFrame({'year':c1,'month':c2,'area':c3.values})
siif2 = pd.concat([siif2,d],axis=0)
sb.lmplot(x='month',y='area',data=siif2).set(title='Ice coverage in Baffin Area: 1997-2017 [km2]');
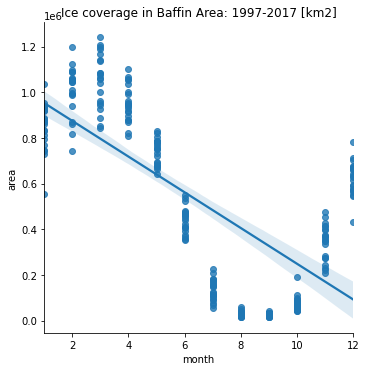
Comentários:
Pode se ver que ao longo do ano, a cobertura de gelo segue um padrão periódico. Todavia, a análise de regressão mostra que há uma tendência de declínio da cobertura.
A flutuação periódica é coerente com as estações do ano.
O declínio se verifica pela queda da amplitude do ciclo periódico.
Normalização dos dados¶
Para evitar a flutuação, normalizaremos a área usando desvios em relação às médias mensais e o percentual relativo à média para o período de anos estudado. A expressão matemática é dada por
onde \(\tilde{\bf a}_i\) é a série contendo valores das áreas normalizadas, \({\bf a}_i\) a série contendo valores das áreas originais, \(\mu_i\) as médias, para o \(i\)-ésimo mês, e \(\mu\) é a média das áreas para todo o período de 20 anos (todos os meses).
import warnings; warnings.simplefilter('ignore')
siif2['arean'] = siif2['area']
for i in np.linspace(1,12,12):
siif2.arean[siif2.month == i] = 100*(siif2.arean[siif2.month == i] - \
siif2.arean[siif2.month == i].mean()) \
/siif2.area.mean()
Plotando os dados normalizados, vemos o seguinte gráfico.
sb.lmplot(x='month',y='arean',data=siif2).set(title='Normalized data');
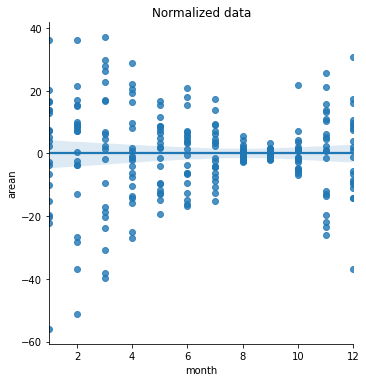
Regressão sobre dados normalizados¶
Realizando uma nova análise de regressão para todo o período de 20 anos, com 95% de índice de confiança, visualizamos uma permanente tendência negativa.
# eixo x como 'float' devido
# à incompatibilidade de lmplot com type 'Int64'
sb.lmplot(x='year',y='arean',data=siif2).set(title='Ice coverage decay: 1997-2017 [km2]');
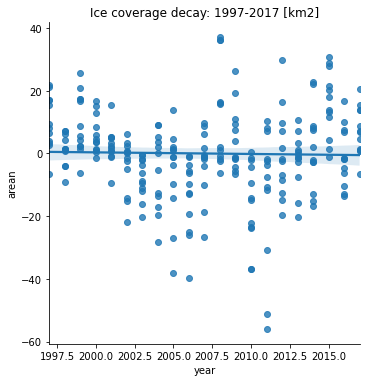
A conclusão do estudo é: embora haja variações de ano a ano, nota-se uma tendência de queda na corbertura da área de gelo na área estudada. Esta diminuição da área de cobertura do gelo leva-nos a crer que o aquecimento global é a causa direta deste fenômeno.
Análise quantitativa¶
No caso anterior, fizemos uma análise qualitativa (visual) de como a área de cobertura de gelo (resposta) diminuiu ao longo do ano (preditor). Entretanto, ainda não temos uma ideia quantitativa deste modelo. Para saber a equação da análise de regressão, podemos utilizar alguns métodos.
scipy.stats.linregress¶
A primeira forma que temos para encontrar a equação do modelo linear é usar scipy.stats.linregress.
res = sts.linregress(siif2['year'],siif2['arean'])
# inclinação, intercept, coef. de correlação
m,b,rho = res.slope,res.intercept,res.rvalue
(m,b,rho)
(-0.051080057519927086, 102.51767544249365, -0.02247112769096617)
plt.scatter(x=siif2['year'],y=siif2['arean'])
# eq. da reta
xx = np.unique(siif2['year'])
yy = m*xx + b
plt.plot(xx,yy,'r-',label=f'y={round(m,2)}x + {round(b,2)}')
plt.legend(loc=3);
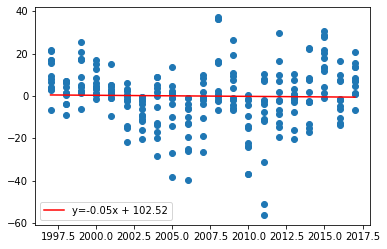
sklearn.linear_model.LinearRegression¶
Outra forma é usar sklearn.linear_model.LinearRegression.
from sklearn.linear_model import LinearRegression
# modelo de ajuste
lr = LinearRegression(fit_intercept=True)
# resolvendo (input deve ser array 2D)
res2 = lr.fit(siif2[['year']],siif2[['arean']])
# slope, intercept
m2,b2 = res2.coef_[0][0], res2.intercept_[0]
m2,b2
(-0.051080057519926975, 102.51767544249344)
Comentários:
Verificamos que os valores de slope (coeficiente angular) e intercept (coeficiente linear) obtidos tanto por
sklearn.linear_model.LinearRegressionquanto porscipy.stats.linregresssão equivalentes.
Preditores e estimadores¶
Estimadores geram predições a partir da análise de regressão. Usando o módulo sklearn (scikit learn), podemos avaliar quão bem o modelo construído se ajusta aos dados conhecidos através de duas métricas bastante populares:
erro quadrático médio (ou MSE, do inglês mean squared error), que fornece uma “média” do quadrado dos \(n\) erros existentes pontualmente entre a série de dados conhecidos \(\{y_i\}\) e a série de dados estimados \(\{\hat{y}_i\}\). O MSE pode ser definido em termos de um preditor ou de um estimador. Ambos os conceitos são levemente distintos. Por conveniência de entendimento, vamos utilizar a definição do primeiro caso, que é:
Observe que, em notação vetorial, o MSE provém de um produto interno, isto é, \(\text{MSE} = \frac{1}{n}({\bf e} \cdot {\bf e})\), com \({\bf e} = {\bf y} - \hat{\bf y}\).
coeficiente de determinação, que mede a “qualidade” do ajuste. Este coeficiente é simplesmente o quadrado do coeficiente de correlação. Comumente, ele é denotado por \(R^2\). Mais comumente, adota-se que \( 0 \leq R^2 \leq 1\). Todavia, dependendo de como ele for definido, valores negativos serão possíveis. Em suma, sua interpretação é a seguinte: se \(R^2 = 0\), o ajuste é o pior possível; se \(R^2 = 1\), o melhor possível.
Vamos calcular essas métricas para um conjunto de dados do sklearn sobre diabetes.
from sklearn import metrics, datasets
# dataset "diabetes"
diabetes_x, diabetes_y = datasets.load_diabetes(return_X_y=True)
# usa apenas uma feature
diabetes_x = diabetes_x[:,np.newaxis,2]
# separação dos dados entre "treinamento" e "teste"
# a predição ocorrerá para o conjunto de "teste"
# preditor
diabetes_x_treino = diabetes_x[:-20] # 422 valores
diabetes_x_teste = diabetes_x[-20:] # 20 valores
# resposta
diabetes_y_treino = diabetes_y[:-20] # 422 valores
diabetes_y_teste = diabetes_y[-20:] # 20 valores
# modelo de RL
linregr = LinearRegression(fit_intercept=True)
# treinamento do modelo
linregr.fit(diabetes_x_treino,diabetes_y_treino)
# predição
diabetes_y_predicao = linregr.predict(diabetes_x_teste)
Agora, verificamos a qualidade do ajuste dos dados pela regressão linear.
# MSE
metrics.mean_squared_error(diabetes_y_teste,diabetes_y_predicao)
2548.0723987259703
# R2
metrics.r2_score(diabetes_y_teste, diabetes_y_predicao)
0.47257544798227136
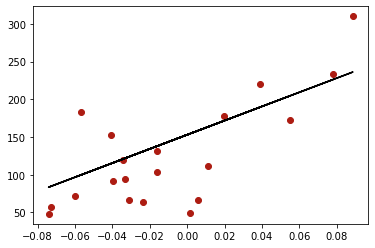
Uma plotagem gráfica simples nos dá a melhor reta de ajuste para os dados segundo o método de mínimos quadrados.
plt.scatter(diabetes_x_teste,diabetes_y_teste,color='#ad1c12')
plt.plot(diabetes_x_teste,diabetes_y_predicao,'-k');
Uma vez que temos à disposição os coeficientes do ajuste, podemos predizer valores em locais desconhecidos.
# slope, intercept
m3,b3 = linregr.coef_[0],linregr.intercept_
print((m3,b3))
# plot
plt.scatter(diabetes_x_teste,diabetes_y_teste,color='#ad1c12')
plt.plot(diabetes_x_teste,diabetes_y_predicao,'-k');
# estimativas
x_est1, x_est2, x_est3 = 0.03, 0.10, 0.3
p = lambda x: m3*x + b3
plt.plot(x_est1,p(x_est1),'sg',ms=10)
plt.plot(x_est2,p(x_est2),'*b',ms=10)
plt.plot(x_est3,p(x_est3),'vm',ms=10);
(938.2378612512633, 152.91886182616167)
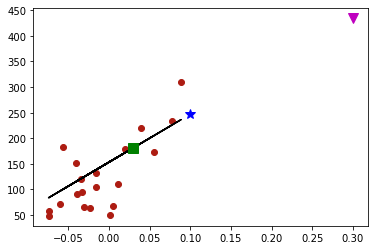
Comentários:
Os 3 pontos são colineares. Ou seja, pertencem à reta.
O triângulo rosa seria considerado uma extrapolação, já que é uma estimativa feita muito “além do conhecido”. Ele segue a tendência linear, mas pode ser uma previsão bastante errônea.
Regressão múltipla¶
Estenderemos a discussão sobre regressão apresentando um exemplo simples de regressão mútlipla. Na regressão múltipla, há mais do que um preditor (covariante) envolvido. Neste caso, em vez de uma reta, o modelo matemático é um hiperplano.
Note
Hiperplano é um conceito generalizado de plano em um espaço vetorial de \(d\) dimensões.
O dataset Advertising.csv, disponibilizado no Kaggle, contém informação sobre orçamentos destinados para anúncios em TV, rádio e jornal, bem como sobre o número de vendas em unidades não declaradas. O objetivo da análise de regressão é saber como esses orçamentos influenciam a venda de produtos.
Para estudar este caso, usaremos o módulo statsmodels.
# importa statsmodels
import statsmodels.api as sm
# carrega dataset
ad = pd.read_csv('../database/Advertising.csv',index_col=0)
ad.head()
| TV | Radio | Newspaper | Sales | |
|---|---|---|---|---|
| 1 | 230.1 | 37.8 | 69.2 | 22.1 |
| 2 | 44.5 | 39.3 | 45.1 | 10.4 |
| 3 | 17.2 | 45.9 | 69.3 | 9.3 |
| 4 | 151.5 | 41.3 | 58.5 | 18.5 |
| 5 | 180.8 | 10.8 | 58.4 | 12.9 |
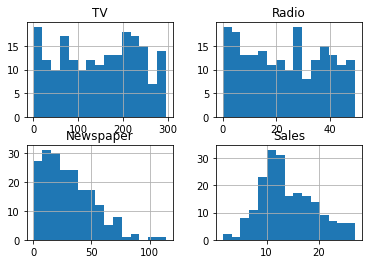
Uma visão geral sobre a distribuição dos dados é obtida com a plotagem múltipla dos histogramas.
# histogramas
ad.hist(bins=15);
Realizamos a análise de regressão linear para verificar se poderíamos usar a variável TV para predizer as vendas.
y_ad = ad['Sales']
X_ad = ad['TV']
X_ad = sm.add_constant(X_ad)
lr = sm.OLS(y_ad,X_ad).fit()
lr.summary()
| Dep. Variable: | Sales | R-squared: | 0.612 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.610 |
| Method: | Least Squares | F-statistic: | 312.1 |
| Date: | Tue, 12 Oct 2021 | Prob (F-statistic): | 1.47e-42 |
| Time: | 15:14:47 | Log-Likelihood: | -519.05 |
| No. Observations: | 200 | AIC: | 1042. |
| Df Residuals: | 198 | BIC: | 1049. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 7.0326 | 0.458 | 15.360 | 0.000 | 6.130 | 7.935 |
| TV | 0.0475 | 0.003 | 17.668 | 0.000 | 0.042 | 0.053 |
| Omnibus: | 0.531 | Durbin-Watson: | 1.935 |
|---|---|---|---|
| Prob(Omnibus): | 0.767 | Jarque-Bera (JB): | 0.669 |
| Skew: | -0.089 | Prob(JB): | 0.716 |
| Kurtosis: | 2.779 | Cond. No. | 338. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# R^2
lr.rsquared
0.611875050850071
Comentário:
\(R^2 \approx 0.61\) indica que cerca de 61% da variância na relação TV-vendas pode ser explicada pelo modelo
lr.
plt.scatter(ad['TV'],ad['Sales']);
plt.xlabel('TV')
plt.ylabel('Vendas');
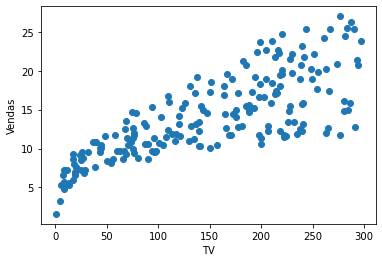
Embora o valor de \(R^2\) seja razoável, vamos repetir a análise, mas agora com a variável Radio.
y_ad2 = ad['Sales']
X_ad2 = ad['Radio']
X_ad2 = sm.add_constant(X_ad2)
lr2 = sm.OLS(y_ad2,X_ad2).fit()
lr2.summary()
| Dep. Variable: | Sales | R-squared: | 0.332 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.329 |
| Method: | Least Squares | F-statistic: | 98.42 |
| Date: | Tue, 12 Oct 2021 | Prob (F-statistic): | 4.35e-19 |
| Time: | 15:14:47 | Log-Likelihood: | -573.34 |
| No. Observations: | 200 | AIC: | 1151. |
| Df Residuals: | 198 | BIC: | 1157. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 9.3116 | 0.563 | 16.542 | 0.000 | 8.202 | 10.422 |
| Radio | 0.2025 | 0.020 | 9.921 | 0.000 | 0.162 | 0.243 |
| Omnibus: | 19.358 | Durbin-Watson: | 1.946 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 21.910 |
| Skew: | -0.764 | Prob(JB): | 1.75e-05 |
| Kurtosis: | 3.544 | Cond. No. | 51.4 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Igualmente, podemos fazer um plot de dispersão.
plt.scatter(ad['Radio'],ad['Sales']);
plt.xlabel('Rádio')
plt.ylabel('Vendas');
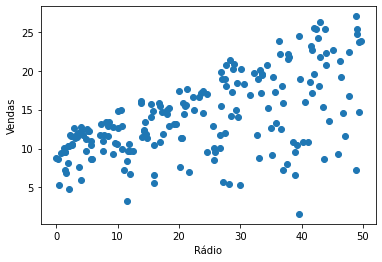
lr2.rsquared
0.33203245544529525
Neste caso, o modelo retorna um valor de \(R^2\) pior do que o anterior. Este valor seria considerado “ruim”. Mas, e se ambos os preditores forem postos juntos no modelo?
Vejamos o que ocorre.
y_ad3 = ad['Sales']
X_ad3 = ad[['TV','Radio']]
X_ad3 = sm.add_constant(X_ad3)
lr3 = sm.OLS(y_ad3,X_ad3).fit()
lr3.summary()
| Dep. Variable: | Sales | R-squared: | 0.897 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.896 |
| Method: | Least Squares | F-statistic: | 859.6 |
| Date: | Tue, 12 Oct 2021 | Prob (F-statistic): | 4.83e-98 |
| Time: | 15:14:47 | Log-Likelihood: | -386.20 |
| No. Observations: | 200 | AIC: | 778.4 |
| Df Residuals: | 197 | BIC: | 788.3 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 2.9211 | 0.294 | 9.919 | 0.000 | 2.340 | 3.502 |
| TV | 0.0458 | 0.001 | 32.909 | 0.000 | 0.043 | 0.048 |
| Radio | 0.1880 | 0.008 | 23.382 | 0.000 | 0.172 | 0.204 |
| Omnibus: | 60.022 | Durbin-Watson: | 2.081 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 148.679 |
| Skew: | -1.323 | Prob(JB): | 5.19e-33 |
| Kurtosis: | 6.292 | Cond. No. | 425. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
lr3.rsquared
0.8971942610828956
Com ambos os preditores, o valor de \(R^2\) saltou para quase 90%, um número melhor! Assim, percebemos que a regressão múltipla resulta em um modelo mais acurado do que os modelos para regressão simples individuais.
Para ver o plano da regressão múltipla, devemos fazer uma plotagem tridimensional.
from mpl_toolkits.mplot3d import Axes3D
# X e Y usando tamanhos de TV and Radio
X_axis, Y_axis = np.meshgrid(np.linspace(ad['TV'].min(), ad['TV']. max(), 100),
np.linspace(ad['Radio'].min(), ad['Radio'].max(), 100))
# equação do hiperplano calculando o eixo Z correspondente (Sales)
# z = a0 + a1x + a2y
Z_axis = lr3.params[0] + lr3.params[1] * X_axis + lr3.params[2] * Y_axis
# cria eixo 3D
fig = plt.figure(figsize=(12, 8)) # figsize refers to width and height of the figure
ax = Axes3D(fig, azim=-50)
# plota o hiperplano
ax.plot_surface(X_axis, Y_axis, Z_axis, cmap=plt.cm.coolwarm, alpha=0.5, linewidth=0)
# plota dispersão
ax.scatter(ad['TV'], ad['Radio'],ad['Sales'])
# labels
ax.set_xlabel('TV'); ax.set_ylabel('Rádio'); ax.set_zlabel('Vendas');
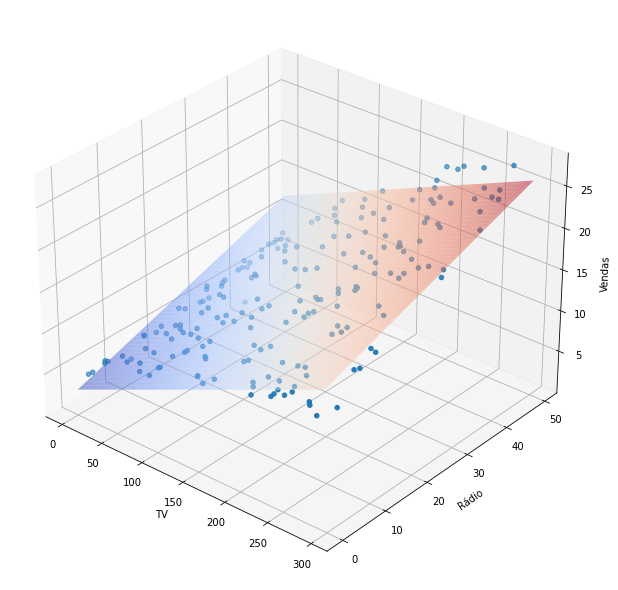
A conclusão da última análise é que as vendas são, de fato, impulsionadas, se houver cada vez mais investimento em propaganda via rádio e televisão.
Estimando valores¶
Digamos que, como um analista de mercado, você tem interesse em prever quanto atingiria em vendas investindo \(t\) e \(r\) unidades monetárias (p.ex. milhares de reais) em anúncios na TV e rádio, respectivamente.
Como fizemos na regressão simples, basta substituir valores na equação do plano e verificar a resposta.
venda_pred = lambda t,r: lr3.params[0] + lr3.params[1]*t + lr3.params[2]*r
venda_pred(102,31)
13.415912077944483
venda_pred(253,44)
22.768814104270994
venda_pred(619,101)
50.23074734862246
Conforme a própria inclinação do plano mostra, à medida que aumentamos o investimento em ambos os canais de divulgação, as vendas aumentam.
Inspeção de multicolinearidade¶
É possível inspecionar a relação entre variáveis (preditores) através de um scatter matrix plot. Por meio dele, gráficos de dispersão são plotados em um formato dois-a-dois. As figuras da diagonal principal mostram apenas histogramas, visto que seria o mesmo que plotar uma variável contra si mesma.
Com a matriz dos gráficos de dispersão, verificamos a multicolinearidade, isto é se pares de variáveis se correlacionam de modo linear. ou não. Para este tipo de plotagem, temos algumas alternativas.
pandas.plotting.scatter_matrix¶
Plota dispersões entre séries de um DataFrame.
pd.plotting.scatter_matrix(ad,figsize=(12,12),grid=True,marker='o', c= ad['Sales']);
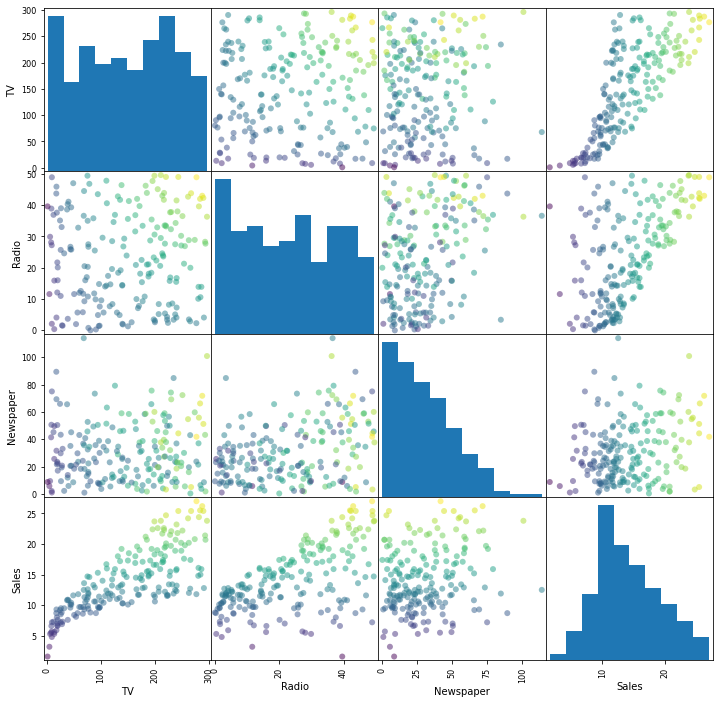
seaborn.pairplot¶
Faz o mesmo que a função anterior. Entretanto, há uma série de opções adicionais.
sb.pairplot(ad);
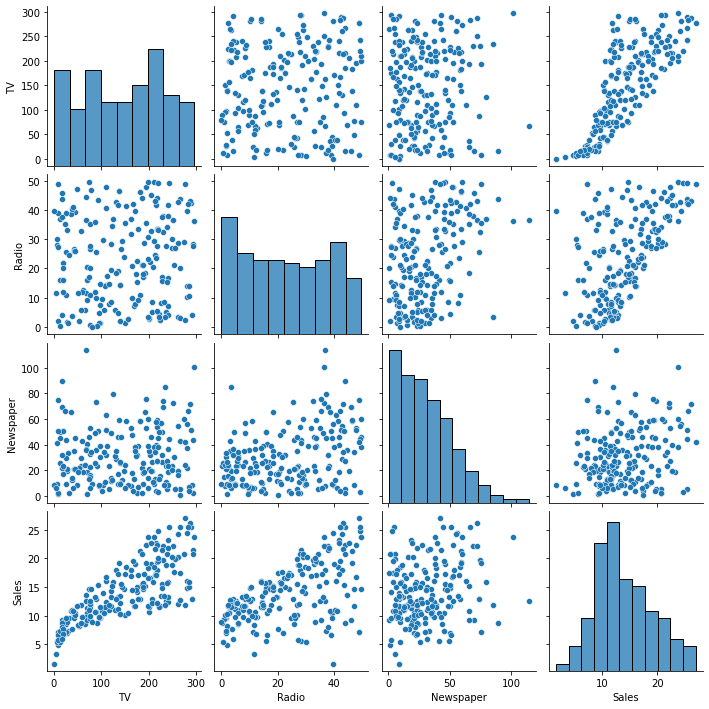
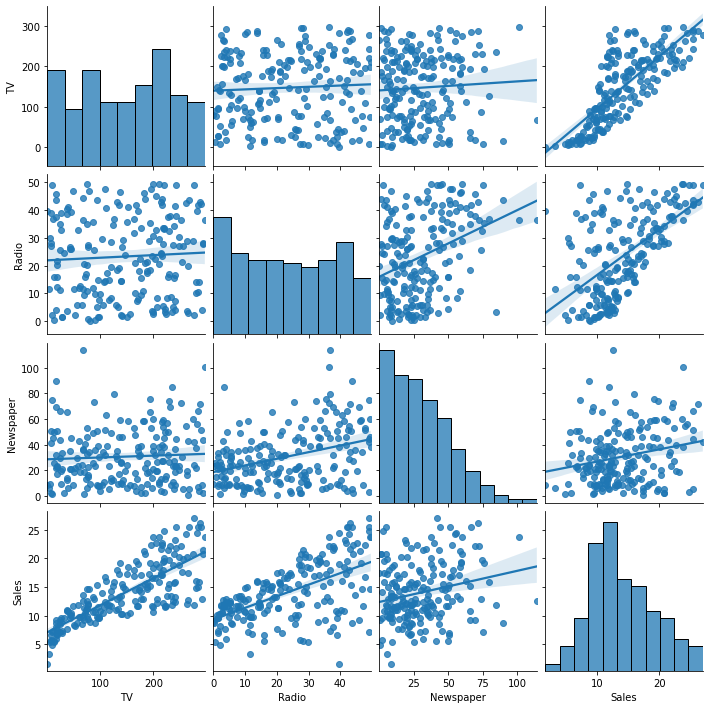
Para incluir as retas de regressão, adicione kind='reg'.
sb.pairplot(ad,kind='reg');
seaborn.heatmap¶
O heat map (mapa de calor) é uma matriz de cores útil para mostrar visualmente coeficientes de correlação entre duas variáveis. As cores quentes representam alta correlação; as frias, baixa correlação.
Podemos criar um mapa de calor para o DataFrame dos anúncios com a ajuda da função pandas.corr().
sb.heatmap(ad.corr(),vmin=0,vmax=1,cmap='RdBu');

Comentários:
vminevmaxsão limitantes para a escala de cores.cmapcontrola o mapa de cores. Para saber as opções possíveis, verifiquehelp(plt.colormaps)
Exercício aplicado¶
Use a série
Newspaperpara criar um modelo de regressão múltipla com os três covariantes do dataset Advertising.csv e faça predições. Note que o seu hiperplano tem imagem real, mas pertence ao \(\mathbb{R}^3\).
