Otimização¶
Introdução¶
Problemas de otimização (POs) são encontrados em diversas situações da Engenharia, em particular na Engenharia de Produção. Em uma linha de produção, por exemplo, a otimização de custos com logística, recursos humanos, matéria-prima são exemplos de onde podemos empregar métodos computacionais para obter soluções ótimas. Entretanto, princípios de otimização são a base de muitos algoritmos e aplicações de inteligência artificial, em particular, no aprendizado de máquina. Máquinas de vetor de suporte (support vector machines) são um exemplo de onde se usa otimização, já que podem ser formuladas como problemas convexos quadráticos.
Problemas de otimização são comumente tratados como problemas de minimização, onde se busca o mínimo global de uma função objetivo (FO) escalar \(f(x)\), visto que maximizar \(f(x)\) é equivalente a minimizar \(-f(x)\).
Entretanto, esses problemas são acompanhados de restrições, que podem ser representadas por uma igualdade ou por uma desigualdade. Quando uma restrição é escrita na forma \(g(x) = 0\), dizemos que \(g(x)\) é uma restrição de igualdade; quando escrita na forma \(h(x) \leq 0\), dizemos que \(h(x)\) é uma restrição de desigualdade.
Neste capítulo, faremos uma breve explanação sobre otimização tomando o cálculo de derivadas e pontos críticos como elementos fundamentais. Utilizaremos recursos de computação simbólica para resolver um problema unidimensional e revisitaremos conceitos aprendidos nas disciplinas de Cálculo.
Classificação de problemas de otimização¶
Problemas de otimização (PO) são classificados com base nas propriedades das funções \(f(x)\), \(g(x)\) e \(h(x)\). Em linhas gerais, um PO pode ser:
univariado (ou unidimensional), se \(x\) é escalar, i.e. \(x \in \mathbb{R}\);
multivariado (ou multidimensional), se \(x\) é um vetor, i.e. \(x \in \mathbb{R}^n\).
linear: se a FO e as restrições são funções lineares. Neste caso, por razões históricas, diz-se que o problema é de programação linear.
não-linear: se a FO e as restrições são funções não-lineares. Neste caso, diz-se que o problema é de programação não-linear.
Com respeito às restrições, um PO pode ainda ser:
irrestrito: quando não se assumem limites para os valores de \(x\).
restrito: quando limites para os valores de \(x\) são impostos.
Aqui trataremos apenas de casos em que \(x \in \mathbb{R}\).
Problemas convexos¶
Sabe-se que problemas não-lineares são muito mais difíceis de resolver do que problemas lineares porque eles podem admitir uma ampla variedade de comportamentos. Um PO não-linear pode ter tanto mínimos locais quanto mínimos globais. Logo, encontrar o mínimo global de uma função \(f(x)\) não-linear exige técnicas aperfeiçoadas.
Neste sentido, uma subclasse de problemas não-lineares que pode ser resolvida eficientemente são os chamados convexos. Em problemas convexos, a função \(f(x)\) é convexa. Mas o que é uma função convexa?
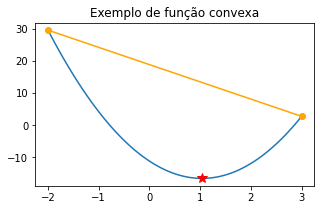
Uma função convexa definida em um intervalo \([a,b]\) é aquela em que todos os seus valores estão abaixo da reta secante que passa pelos pontos \((a,f(a))\) e \((b,f(b)\). Isto, por sua vez, garante que ela contenha somente um mínimo global.
Importaremos os seguintes módulos:
import numpy as np
import matplotlib.pyplot as plt
import sympy as sy
sy.init_printing()
Exemplo: a função \(f(x) = 3x^2 - 0.36x - 11.2\) é convexa em \([-2,3]\).
# domínio
a,b = -2,3
x = np.linspace(a,b,100)
# função e valores nos extremos
f = lambda x: 5*x**2 - 10.36*x - 11.2
fa,fb = f(a),f(b)
# reta secante
s = fa + (fb - fa)/(b - a)*(x - a)
# ponto de mínimo: -b/(2a)
xmin = 10.36/10
# plotagem de funções
plt.figure(figsize=(5,3))
plt.plot(x,f(x))
plt.plot(x,s,color='#ffa500')
# pontos da secante
plt.plot(a,f(a),'o',color='#ffa500')
plt.plot(b,f(b),'o',color='#ffa500')
# ponto de mínimo
plt.plot(xmin,f(xmin),'*r',ms=10);
plt.title('Exemplo de função convexa');
Exemplo: a função \(p(x) = 10x^2\textrm{sen}(6x) - 10.36\exp(x/8) - 11.2\) não é convexa em \([-2,3]\).
# função
p = lambda x: 10*x**2*np.sin(6*x) - 10.36*x*np.exp(x/8) - 11.2
# extremos
pa,pb = p(a),p(b)
# secante
t = pa + (pb - pa)/(b - a)*(x - a)
# plotagem de funções
plt.figure(figsize=(5,3))
plt.plot(x,p(x))
plt.plot(x,t,color='#ffa500')
# pontos da secante
plt.plot(a,p(a),'o',color='#ffa500')
plt.plot(b,p(b),'o',color='#ffa500')
# mínimos locais
xloc = [-1.33868618,0.88811853,1.87451904]
for xl in xloc:
plt.plot(xl,p(xl),'or');
# mínimo global
xmin2 = 2.90547127
plt.plot(xmin2,p(xmin2),'*r',ms=10);
plt.title('Exemplo de função não convexa');
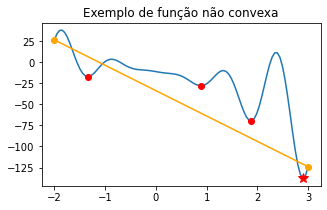
Como vemos acima, a função \(p(x)\) admite 3 mínimos locais e um mínimo global. Pense um pouco sobre que estratégia computacional você utilizaria para encontrar os mínimos locais. Mais adiante mostraremos como localizar o mínimo global para funções univariadas contínuas (quando possível).
Pontos de sela¶
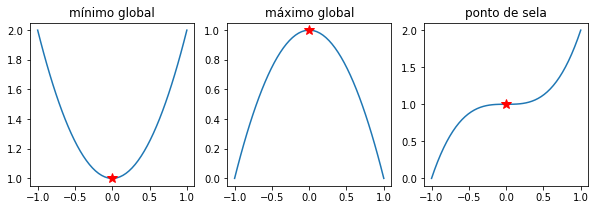
Como vimos acima, a convexidade de uma função é uma propriedade muito importante para que um mínimo global seja localizado. Como sabemos do Cálculo, pontos de máximo ou mínimo identificam-se como pontos críticos de uma função nos quais a primeira derivada da função se anula.
Casos particulares onde a derivada de uma FO anula-se mas o ponto não pode ser definido como de mínimo ou máximo podem ocorrer. Tais situações implicam a existência dos chamados pontos de sela. Uma função com um único ponto de sela, por exemplo, não admitirá mínimo global nem mínimo local. Para testarmos se um ponto crítico é um ponto de sela, devemos verificar o sinal da segunda derivada da função. Uma das seguintes situações deve ser obtida em um ponto crítico \(x^*\):
ponto de mínimo: \(f''(x^*) > 0\)
ponto de máximo: \(f''(x^*) < 0\)
ponto de sela: \(f''(x^*) = 0\)
Exemplo: qualquer função quadrática admite ou um ponto de mínimo ou de máximo. A função \(f(x) = x^3\) possui um ponto de sela em \(x^* = 0\).
x = np.linspace(-1,1)
plt.figure(figsize=(10,3))
plt.subplot(131)
plt.plot(x,x**2 + 1)
plt.plot(0,1,'r*',ms=10)
plt.title('mínimo global')
plt.subplot(132)
plt.plot(x,-x**2 + 1)
plt.plot(0,1,'r*',ms=10)
plt.title('máximo global')
plt.subplot(133)
plt.plot(x,x**3 + 1)
plt.plot(0,1,'r*',ms=10)
plt.title('ponto de sela');
Otimização univariada¶
Como dissemos anteriormente, a otimização univariada visa resolver um problema de minimização tomando uma FO que depende apenas de uma variável. Matematicamente, podemos descrever este problema da seguinte forma:
Em geral, \(x\) é uma variável de decisão, isto é, uma quantidade que pode ser ajustada livremente (ex. comprimentos, áreas, ângulos etc.).
As técnicas utilizadas para a resolução de um problema desse tipo são baseadas em métodos analíticos (busca pelos zeros das derivadas) ou em métodos computacionais (determinação de raízes por processos iterativos). Métodos chamados de root finding são estudados em um curso introdutório de Métodos Numéricos.
Para exemplificar, usaremos uma abordagem analítica por meio de computação simbólica (módulo sympy) para resolver um problema que pode ser exibido como de otimização univariada.
Problema resolvido¶
Consideremos o seguinte problema: maximizar a área do retângulo inscrito em uma elipse.
Resolução¶
Em primeiro lugar, escreveremos este problema em linguagem matemática. Sabemos que a área de um retângulo com vértice esquerdo inferior na origem da elipse e com vértice direito superior no ponto \((x,y)\) da elipse que está no primeiro quadrante é dada por \(A_r = xy\). Logo, a área do retângulo inscrito na elipse será \(A = 4xy\).
A área \(A\) pode ser escrita em termos de \(y\). Uma vez que a equação da elipse (centrada na origem) é dada por
podemos resolver a equação da elipse para \(x\) (ou \(y\)) e substituir esta solução na expressão da área para ter uma função \(A(x)\) (ou \(A(y)\)). Se escolhermos \(x\), o problema de otimização pode ser escrito como:
Notemos que maximizar \(A(x)\) equivale a minimizar \(-A(x)\).
Na busca do ponto de mínimo \(x^{*}\), usaremos computação simbólica.
Primeiramente, criamos variáveis simbólicas que representem as variáveis de interesse do problema e a expressão da área total.
# cria variáveis simbólicas
x,y,a,b = sy.symbols('x,y,a,b')
# área do retângulo no 1o. quadrante é xy
# logo, área total é 4xy
A = -4*x*y
A
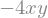
Em seguida, resolvemos a equação da elipse para a variável \(y\) utilizando a função sympy.solve.
# resolve equação da elipse para y
sol = sy.solve(x**2/a**2 + y**2/b**2 - 1,y)
sol[0],sol[1]

Duas soluções são possíveis para \(y\). Porém, como o nosso ponto de referência sobre a elipse está no primeiro quadrante, tomamos a expressão para \(y > 0\) e a substituímos na expressão da área de forma a obter uma expressão univariada \(A(x)\).
# substitui expressão de y positivo em A para ter -A(x)
A = A.subs({'y':sol[1]})
A
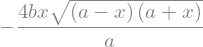
Localizaremos o ponto crítico da função a partir da derivada \(A'(x)\). Derivando \(A\) em relação a \(x\), obtemos:
# deriva -A(x) com a,b constantes
dAdx = A.diff(x)
dAdx
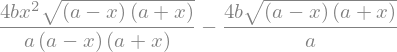
Em seguida, buscamos \(x^{*}\) tal que \(A'(x^{*}) = \frac{dA}{dx}(x^{*}) = 0\).
# resolve A'(x*) = 0
sol_x = sy.solve(dAdx,x)
sol_x
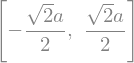
Duas soluções, são possíveis, porém, podemos verificar qual ponto de crítico, de fato, é o que minimizará \(-A(x)\) através da análise da concavidade. Então, calculamos \(A''(x)\), para cada ponto crítico.
# testa A''(x) para os dois pontos
dAdx2 = dAdx.diff(x)
dAdx2.subs(x,sol_x[0]).simplify(),dAdx2.subs(x,sol_x[1]).simplify()
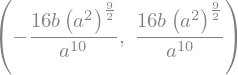
Uma vez que a segunda solução verifica a concavidade positiva, temos que o ponto crítico \(x^{*}\) é:
# concavidade para cima => ponto de mínimo
xs = sol_x[1]
xs
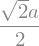
Usando este valor na equação da elipse, obtemos a ordenada correspondente:
# resolve para y > 0
ys = sy.solve(xs**2/a**2 + y**2/b**2 - 1,y)[1]
ys
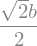
Por fim, substituindo \(x^{*}\) na expressão da área, temos que \(A_{max}\) é:
# área máxima
A_max = A.subs(x,xs)
A_max
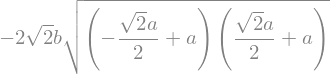
ou, de forma, simplificada,
# simplificando
A_max.simplify()

Conclusão¶
A área do retângulo inscrito na elipse será máxima quando \(x = \frac{\sqrt{2}}{2}a\) e \(y = \frac{\sqrt{2}}{2}b\). Portanto, \(A_{max} = 2ab\), para comprimentos \(a\) e \(b\) de semi-eixo maior e menor.
Estudo paramétrico de geometria¶
No gráfico abaixo, plotamos a variação das áreas de retângulos inscritos em uma elipse arbitrária com semi-eixos \(a\) e \(b\) em função do comprimento \(x\) da meia-base do retângulo até o limite da meia-base do retângulo de área máxima. Adicionalmente, plotamos a variação do comprimento da diagonal do retângulo. A constante \(A_{elip}\) é a área da elipse.
Você pode alterar os parâmetros de construção de elipse, o número de valores para \(x\) e realizar uma nova análise dos parâmetros.
# semi-eixos da elipse
a,b = 10,2
# no. de retângulos inscritos
nx = 40
# base variável do retângulo
X = np.linspace(0,np.sqrt(2)/2*a,nx)
# área da elipse
e = np.pi*a*b
# áreas dos retângulos
R = []
H = []
for x in X:
y = b*np.sqrt(1 - x**2/a**2)
r = 4*x*y
h = np.hypot(2*x,2*y) # diagonal do retângulo
R.append(r)
H.append(h)
# plotagem
fig,ax1 = plt.subplots(figsize=(6,4))
ax1.plot(X,R,'sb',mec='w',alpha=0.8,label='$A_{ret}(x)$')
ax1.plot(X,np.full(X.shape,2*a*b),'--r',alpha=0.8,label='$A_{max}$')
ax1.plot(X,np.full(X.shape,e),'-',alpha=0.8,label='$A_{elip}$')
ax1.legend(fontsize=10)
# labels
plt.xlabel('$x$ [compr. base ret. inscrito]')
plt.ylabel('$A$ [áreas]');
ax2 = ax1.twinx()
ax2.plot(X,H,'og',mec='w',alpha=0.8,label='$h_{ret}(x)$')
ax2.legend(loc=5,ncol=1,fontsize=10)
plt.ylabel('$h$ [compr. diag ret.]');
plt.suptitle('Variação de áreas e diagonais: elipse x retângulo inscrito\n');
plt.title(f'Elipse: $x^2/({a:.1f})^2 + y^2/({b:.1f})^2 = 1$',fontsize=10);

