Distribuições¶

A estatística descritiva é limitada para resumir dados, visto que dados com características completamente distintas podem ter os mesmos valores para média, mediana e variância, por exemplo.

Uma forma aprofundada de reconhecer as características dos dados é inspecionar a sua distribuição. Neste capítulo, discutiremos algumas distribuições e outras técnicas de exploração de dados.

import pandas as pd
import numpy as np
import scipy as sp
import seaborn as sb
import matplotlib.pyplot as plt

import warnings
warnings.filterwarnings('ignore')

Função massa de probabilidade¶

A função massa de probabilidade (FMP) associa uma probabilidade à ocorrência de um certo valor dentro de um espaço de resultados. Podemos entender a FMP como um histograma normalizado. Isto é, todas as frequências são divididas pelo número de amostras.

Para estudar a FMP e os demais conceitos neste capítulo, usaremos um banco de dados que contém dados sobre adultos americanos, tais como idade, nível de escolaridade, ocupação, estado civil, entre outros.

Primeiramente, carregamos o dataset.

adults = pd.read_csv('../database/adults.csv',skiprows=1)
adults.head()

	age	type-employer	fnlwgt	education	education_num	marital	occupation	relationship	race	sex	capital_gain	hr_per_week	country	income
0	39	State-gov	77516	Bachelors	13	Never-married	Adm-clerical	Not-in-family	White	Male	2174	40	United-States	<=50K
1	50	Self-emp-not-inc	83311	Bachelors	13	Married-civ-spouse	Exec-managerial	Husband	White	Male	0	13	United-States	<=50K
2	38	Private	215646	HS-grad	9	Divorced	Handlers-cleaners	Not-in-family	White	Male	0	40	United-States	<=50K
3	53	Private	234721	11th	7	Married-civ-spouse	Handlers-cleaners	Husband	Black	Male	0	40	United-States	<=50K
4	28	Private	338409	Bachelors	13	Married-civ-spouse	Prof-specialty	Wife	Black	Female	0	40	Cuba	<=50K

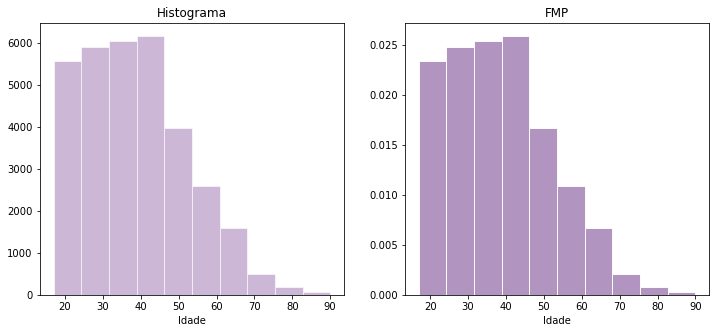
Comparemos a distribuição da variável idade por histograma e pela PMF.

plt.figure(figsize=(12,5))

# histograma
plt.subplot(121)
idade = adults['age']
idade.hist(alpha=.6,bins=10,
           color='#aa88bb',edgecolor='w',
           grid=False);
plt.xlabel('Idade')
plt.title('Histograma')

# FMP
plt.subplot(122)
idade = adults['age']
idade.hist(alpha=.9,bins=10,density=True,
           color='#aa88bb',edgecolor='w',
           grid=False);

plt.xlabel('Idade')
plt.title('FMP');

Função distribuição cumulativa¶

A função distribuição cumulativa (CDF) calcula a probabilidade de uma variável com uma dada distribuição de probabilidade ter um valor menor ou igual a \(x\). Em outras palavras, para calcularmos \(CDF(x)\) para um valor particular \(x\), devemos computar a fração dos valores na amostra que são menores ou iguais a \(x\). A CDF é similar ao conceito de percentil, mas a resposta é um valor no intervalo [0,1], em vez de um ranque na faixa 0-100.

Considerando um array de amostras t e o dado valor \(x\), que não necessariamente está em t, podemos implementar uma função CDF da seguinte forma:

# implementação da CDF
def CDF(t,x):
    c = 0 # contagem
    for ti in t: # cada valor na amostra
        if ti <= x:
            c += 1
    prob = c / len(t) # probabilidade
    return prob

Vejamos um exemplo simples.

# amostra
t = [1,2,3,3,5,7]

CDF(t,2), CDF(t,3), CDF(t,5)

(0.3333333333333333, 0.6666666666666666, 0.8333333333333334)

Comentários:

A probabilidade de se encontrar um valor menor ou igual a 2 em t é de 33,3%.
A probabilidade de se encontrar um valor menor ou igual a 3 em t é de 66,6%.
A probabilidade de se encontrar um valor menor ou igual a 5 em t é de 83,3%.

Para valores fora da amostra:

CDF(t,3.45), CDF(t,1.11)

(0.6666666666666666, 0.16666666666666666)

Se \(x\) for menor do que o menor valor de t, CDF(x) = 0; se \(x\) for maior do que o maior valor de t, CDF(x) = 1.

CDF(t,-4), CDF(t,0.8), CDF(t,7.5), CDF(t,12)

(0.0, 0.0, 1.0, 1.0)

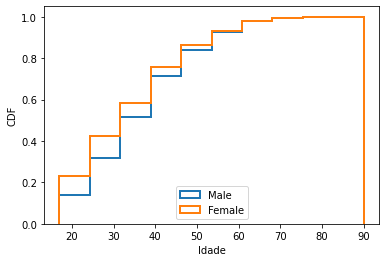
A CDF é uma função step:

sex = adults['sex']
im = idade[sex == ' Male']
fm = idade[sex == ' Female']

im.hist(density=True,cumulative=True,
        histtype='step',grid=False,linewidth=2,
        label='Male')
fm.hist(density=True,cumulative=True,
        histtype='step',grid=False,linewidth=2,
        label='Female')

plt.xlabel('Idade')
plt.ylabel('CDF')
plt.legend(loc=8);

Medição de assimetria¶

A assimetria das distribuições pode ser medida pelo coeficiente de Pearson, dado por:

\[p = 3(\mu - \theta)\sigma,\]

onde \(\mu\) é a média, \(\theta\) é a mediana e \(\sigma\) é o desvio padrão.

Podemos defini-lo como:

# coeficiente de pearson
def p(x):
    return 3*( x.mean() - x.median() )*x.std()

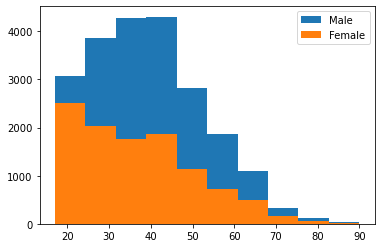
A seguir calculamos o coeficiente de Pearson para a série de idades para homens e mulheres.

p(im), p(fm)

(57.50230041174153, 78.12203531109172)

Comparemos com os histogramas.

im.hist(grid=False,label='Male')
fm.hist(grid=False,label='Female')
plt.legend();

A interpretação da assimetria é a seguinte:

Na assimetria à direita (ou positiva), a moda e a mediana localizam-se à esquerda da média. Isto significa que o histograma é mais denso à esquerda.
Na assimetria à esquerda (ou negativa), a moda e a mediana localizam-se à direita da média. Isto significa que o histograma é mais denso à direita.
Coeficientes de assimetria positivos explicam assimetria à direita.
Coeficientes de assimetria negativos explicam assimetria à esquerda.
Coeficientes de assimetria nulos explicam simetria (distribuição normal).

Comentários:

No exemplo anterior, o coeficiente de Pearson maior para a distribuição de idades entre mulheres mostra que ela é mais assimétrica do que a distribuição de idades para mulheres.

Distribuições contínuas¶

Distribuições baseadas em observações de amostras finitas são chamadas de distribuições empíricas, a exemplo da FMP anterior. Em muitas situações, necessitamos de distribuições contínuas. No caso de funções contínuas, a FMP é generalizada para a função densidade de probabilidade (PDF). A PDF é definida por meio de integração.

Distribuição exponencial¶

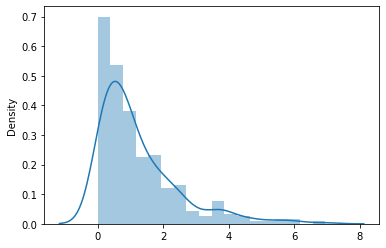
A distribuição exponencial (DE) serve para medir tempos entre eventos, que são chamados de “tempos de chegadas” (inter-arrival times). Se os eventos têm a mesma probabilidade de ocorrer a qualquer momento, a distribuição dos tempos de chegadas tende a se parecer com uma distribuição exponencial.

DEs são úteis para descrever: o tempo de realização de uma prova, o tempo de vida de aparelhos, o tempo de espera em restaurantes, o tempo para realizar uma prova.

A CDF e a PDF de uma distribuição exponencial são definidas por:

\[CDF(x) = 1 - e^{-\lambda x}, \ \ \ PDF(x) = \lambda e^{-\lambda x},\]

onde \(\lambda\) é um parâmetro que define o formato da distribuição.

Uma DE tem:

média = \(1/\lambda\)
variância = \(1/\lambda^2\)
mediana = \(\ln(2)/\lambda.\)

Para plotar uma DE aleatoriamente, podemos utilizar o numpy

# usando numpy
lamb = 1.3
n = 300
de = np.random.exponential(scale=lamb,size=n)
sb.distplot(de);

ou o scipy

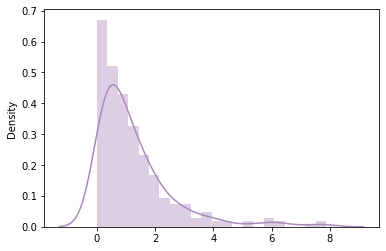
# usando scipy
des = sp.random.exponential(scale=lamb,size=n);
sb.distplot(des,color='#aa88bb');

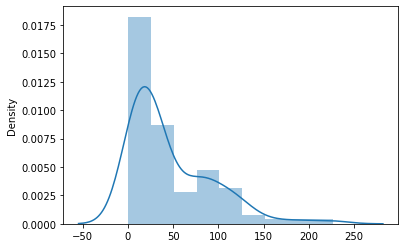
No próximo exemplo, usamos um valor bem maior de \(\lambda\):

lamb = 50.3
n = 100
de = np.random.exponential(scale=lamb,size=n)
sb.distplot(de);

Distribuição normal¶

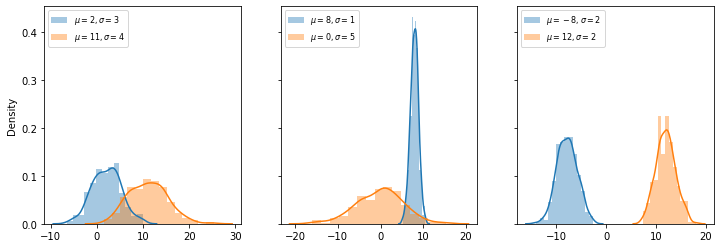
A distribuição normal, ou distribuição Gaussiana, possui um formato particularmente simétrico. Ela é a distribuição mais comumente empregada para representar fenômenos econômicos, naturais, sociais, entre outros. Enquanto a CDF para a distribuição normal dependa de integrais que não podem ser expressas em termos de funções elementares, a sua função densidade de probabilidade é dada por

\[PDF(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}}e^{- \frac{(x-\mu)^2}{2\sigma^2}},\]

onde \(\mu\) é a média e \(\sigma\) o desvio padrão de uma série de dados.

À medida que os valores de \(\mu\) e \(\sigma\) são alterados, a forma de “sino” da distribuição “alarga”, “afina”, “estica” ou se “contrai”.

Vejamos como gerar DNs através do scipy.

n = 300
mu, sigma = 2, 3

fig, ax = plt.subplots(1,3,sharey=True,figsize=(12,4))
lab = lambda mu,sigma: f'$\mu={mu},\sigma={sigma}$'

dn = sp.random.normal(mu,sigma,n) 
sb.distplot(dn,ax=ax[0],label=lab(mu,sigma));
dn = sp.random.normal(mu+9,sigma+1,n) 
sb.distplot(dn,ax=ax[0],label=lab(mu+9,sigma+1));
ax[0].legend(loc=2,fontsize=8)

dn = sp.random.normal(mu+6,sigma-2,n) 
sb.distplot(dn,ax=ax[1],label=lab(mu+6,sigma-2));
dn = sp.random.normal(mu-2,sigma+2,n) 
sb.distplot(dn,ax=ax[1],label=lab(mu-2,sigma+2));
ax[1].legend(loc=2,fontsize=8)

dn = sp.random.normal(mu-10,sigma-1,n) 
sb.distplot(dn,ax=ax[2],label=lab(mu-10,sigma-1));
dn = sp.random.normal(mu+10,sigma-1,n) 
sb.distplot(dn,ax=ax[2],label=lab(mu+10,sigma-1));
ax[2].legend(loc=2,fontsize=8);

A CDF para essas distribuições pode ser plotada adicionado kde_kws={'cumulative':True} na função distplot do seaborn. Para remover o histograma, basta configurar hist=False.

fig, ax = plt.subplots(1,3,sharey=True,figsize=(12,4))

dn = sp.random.normal(mu,sigma,n) 
sb.distplot(dn,ax=ax[0],hist=False,kde_kws={'cumulative':True},
            label=lab(mu,sigma));
dn = sp.random.normal(mu+9,sigma+1,n) 
sb.distplot(dn,ax=ax[0],hist=False,kde_kws={'cumulative':True},
            label=lab(mu+9,sigma+1));
ax[0].legend(loc='best',fontsize=8)

dn = sp.random.normal(mu+6,sigma-2,n) 
sb.distplot(dn,ax=ax[1],hist=False,kde_kws={'cumulative':True},
            label=lab(mu+6,sigma-2));
dn = sp.random.normal(mu-2,sigma+2,n) 
sb.distplot(dn,ax=ax[1],hist=False,kde_kws={'cumulative':True},
            label=lab(mu-2,sigma+2));
ax[1].legend(loc='best',fontsize=8)

dn = sp.random.normal(mu-10,sigma-1,n) 
sb.distplot(dn,ax=ax[2],hist=False,kde_kws={'cumulative':True},
            label=lab(mu-10,sigma-1));
dn = sp.random.normal(mu+10,sigma-1,n) 
sb.distplot(dn,ax=ax[2],hist=False,kde_kws={'cumulative':True},
            label=lab(mu+10,sigma-1));
ax[2].legend(loc='best',fontsize=8);

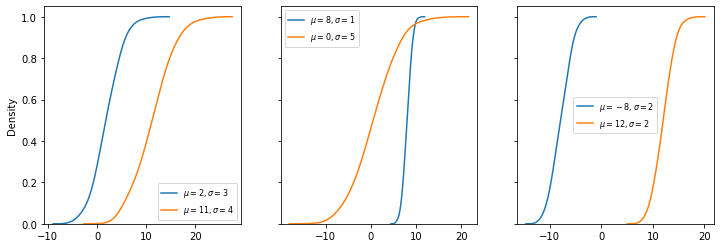
Distribuição logística¶

A distribuição logística (DL) é interessante para fundamentar aplicações de aprendizagem de máquina, principalmente em problemas envolvendo regressão logística e redes neurais. A DL é utilizada para descrever fenômenos associados a crescimento ou queda. Modelos biológicos são um exemplo. A função de distribuição geral de uma DL é:

\[PDF(x) = \frac{e^{-\frac{(x-\mu)}{s}}}{s(1 + e^{-\frac{(x-\mu)}{s}})^2},\]

para uma a média \(\mu\) e o parâmetro \(s\).

Com o scipy, podemos gerar DLs da mesma forma que as distribuições anteriores.

mu, s = 2, 3

fig, ax = plt.subplots(1,3,sharey=True,figsize=(12,4))
lab = lambda mu,s: f'$\mu={mu},s={s}$'

dn = sp.random.logistic(mu,s,n) 
sb.distplot(dn,ax=ax[0],label=lab(mu,s));
dn = sp.random.logistic(mu+9,s+1,n) 
sb.distplot(dn,ax=ax[0],label=lab(mu+9,s+1));
ax[0].legend(loc=2,fontsize=8)

dn = sp.random.logistic(mu+6,s-2,n) 
sb.distplot(dn,ax=ax[1],label=lab(mu+6,s-2));
dn = sp.random.logistic(mu-2,s+2,n) 
sb.distplot(dn,ax=ax[1],label=lab(mu-2,s+2));
ax[1].legend(loc=2,fontsize=8)

dn = sp.random.logistic(mu-10,s-1,n) 
sb.distplot(dn,ax=ax[2],label=lab(mu-10,s-1));
dn = sp.random.logistic(mu+10,sigma-1,n) 
sb.distplot(dn,ax=ax[2],label=lab(mu+10,s-1));
ax[2].legend(loc=2,fontsize=8);

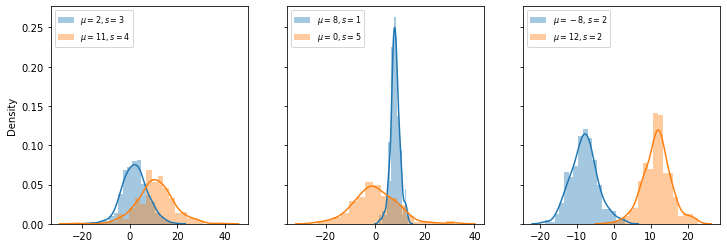
fig, ax = plt.subplots(1,3,sharey=True,figsize=(12,4))

dn = sp.random.logistic(mu,sigma,n) 
sb.distplot(dn,ax=ax[0],hist=False,kde_kws={'cumulative':True},
            label=lab(mu,sigma));
dn = sp.random.logistic(mu+9,sigma+1,n) 
sb.distplot(dn,ax=ax[0],hist=False,kde_kws={'cumulative':True},
            label=lab(mu+9,sigma+1));
ax[0].legend(loc='best',fontsize=8)

dn = sp.random.logistic(mu+6,sigma-2,n) 
sb.distplot(dn,ax=ax[1],hist=False,kde_kws={'cumulative':True},
            label=lab(mu+6,sigma-2));
dn = sp.random.logistic(mu-2,sigma+2,n) 
sb.distplot(dn,ax=ax[1],hist=False,kde_kws={'cumulative':True},
            label=lab(mu-2,sigma+2));
ax[1].legend(loc='best',fontsize=8)

dn = sp.random.logistic(mu-10,sigma-1,n) 
sb.distplot(dn,ax=ax[2],hist=False,kde_kws={'cumulative':True},
            label=lab(mu-10,sigma-1));
dn = sp.random.logistic(mu+10,sigma-1,n) 
sb.distplot(dn,ax=ax[2],hist=False,kde_kws={'cumulative':True},
            label=lab(mu+10,sigma-1));
ax[2].legend(loc='best',fontsize=8);

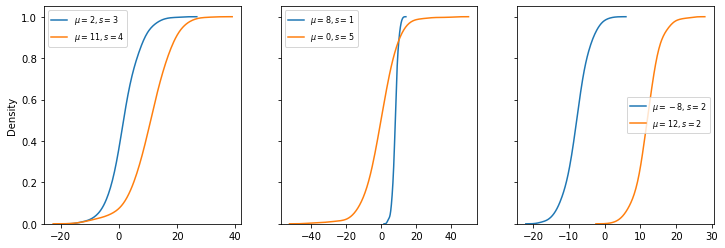
Estimadores de densidade de kernel¶

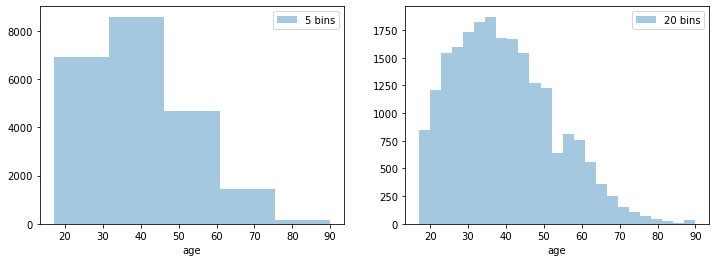
Histogramas possuem o ponto de fraco de definir intervalos de classe (binning). Dependendo dos dados com que trabalhamos, métodos diferentes de binning podem levar a interpretações diferentes, visto que a plotagem visual pode ser diferente.

Um kernel especifica o formato da distribuição em cada ponto e a largura de banda controla o tamanho do kernel. O propósito de um kernel density estimator (KDE) é buscar uma distribuição contínua do conjunto de dados, quando nosso interesse é apenas fazer uma inspeção geral nos dados.

Há diversos tipos de kernel e rotinas implementados em Python. Entretanto, vamos utilizar os KDEs do módulo scikit-learn.

Antes disso, vejamos o efeito do binning sobre os dados.

fig, ax = plt.subplots(1,2,sharey=False,figsize=(12,4))
sb.distplot(im,ax=ax[0],bins=5,kde=False,label='5 bins')
ax[0].legend()
sb.distplot(im,ax=ax[1],bins=25,kde=False,label='20 bins')
ax[1].legend();

Os kernels disponíveis no scikit-learn são obtidos a partir da classe KernelDensity.

from sklearn.neighbors import KernelDensity

X_plot = np.linspace(-6, 6, 200)[:, None]
X_src = np.zeros((1, 1))

fig, ax = plt.subplots(2, 3, sharex=True, sharey=True,figsize=(8,5))
fig.subplots_adjust(left=0.05, right=0.95, hspace=0.2, wspace=0.2)


def ff(x, loc):
     if x == 0:
        return "0"
     elif x == 1:
        return "h"
     elif x == -1:
        return "-h"
     else:
        return f"%ih" % x


for i, kernel in enumerate(
    ["gaussian", "tophat", "epanechnikov", "exponential", "linear", "cosine"]
):
    axi = ax.ravel()[i]
    log_dens = KernelDensity(kernel=kernel).fit(X_src).score_samples(X_plot)
    axi.fill(X_plot[:, 0], np.exp(log_dens), "-k", fc='#aa88bb')
    axi.set_title(kernel)
    
    axi.xaxis.set_major_formatter(plt.FuncFormatter(ff))
    axi.xaxis.set_major_locator(plt.MultipleLocator(1))
    axi.yaxis.set_major_locator(plt.NullLocator())
    
    axi.set_xlim(-2.9, 2.9)

plt.suptitle("Kernels disponíveis :: scikit-learn");

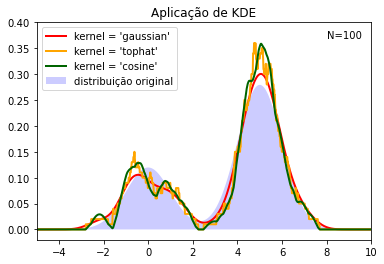
from scipy.stats import norm

N = 100 # amostras
band = 0.5 # largura de banda
kernels = ["gaussian", "tophat", "cosine"]

np.random.seed(1)
X = np.concatenate(
    (np.random.normal(0, 1, int(0.3 * N)),
     np.random.normal(5, 1, int(0.7 * N))))[:, np.newaxis]

Xp = np.linspace(-5, 10, 1000)[:, np.newaxis]

true_dens = 0.3 * norm(0,1).pdf(Xp[:, 0]) + 0.7 * norm(5, 1).pdf(Xp[:, 0])

fig, ax = plt.subplots()
ax.fill(Xp[:, 0], true_dens, fc="blue", alpha=0.2, label="distribuição original")
colors = ["red", "orange", "darkgreen"]

lw = 2

for color, kernel in zip(colors, kernels):
    kde = KernelDensity(kernel=kernel, bandwidth=band).fit(X)
    log_dens = kde.score_samples(Xp)
    ax.plot(
        Xp[:, 0],
        np.exp(log_dens),
        color=color,
        lw=lw,
        linestyle="-",
        label="kernel = '{0}'".format(kernel),
    )

ax.text(8, 0.37, "N={0}".format(N))

ax.legend(loc="upper left")

ax.set_xlim(-5, 10)
ax.set_ylim(-0.02, 0.4)
plt.title('Aplicação de KDE');

Análise de regressão Aprendizado de máquina - I

Introdução à Ciência de Dados