Estatística Descritiva¶
Estatística é um domínio do conhecimento que se preocupar em compreender dados. Ela se ampara solidamente em métodos matemáticos e pode ser dividida em dois ramos: i) estatística inferencial, que se preocupa em tirar conclusões dos dados analisados, e ii) estatística descritiva, que procura apenas descrever dados quantitativamente valendo-se de conceitos como “amostra” e “população” e apresentado os dados de modo gerenciável.
População e amostra¶
Uma população é uma coleção de objetos, ou unidades, sobre a qual a informação é procurada. Uma amostra é uma parte da população observada.
Análise de dados exploratória¶
Dados extraídos a partir de medições realizadas em amostras representativas constituem o que chamamos de observações. Medições e categorias representam uma distribuição amostral de uma certa variável, as quais podem ser usadas para representar aproximadamente a distribuição populacional dessa variável. O papel da análise de dados exploratória é dar subsídios para visualizar e resumir distribuições amostrais de modo que possamos levantar hipóteses sobre a população envolvida.
Descrição de dados¶
Neste capítulo, apresentaremos vários métodos desenvolvidos para Series e DataFrames relacionados à Estatística Descritiva. Começaremos importando as bibliotecas pandas e numpy.
import numpy as np
import pandas as pd
Distribuição de frequência¶
Uma distribuição de frequência é uma tabela que contém um resumo das observações. A distribuição é organizada em uma tabela que contém intervalos de classe (grupos) e frequências correspondentes.
Note
Intervalos de classe são formados por um limite inferior L e um superior S. Eles costumam ser expressos por um “T” horizontal, em que \(L \vdash S\) indica o intervalo \([L,S)\).
Abaixo vemos um exemplo simplificado de tabela de distribuição de frequência (número de alunos) e intervalos de classe de alturas para uma amostra de alunos.
Altura (m) |
No. de alunos |
|---|---|
1,50 \(\vdash\) 1,60 |
5 |
1,60 \(\vdash\) 1,70 |
15 |
1,70 \(\vdash\) 1,80 |
17 |
1,80 \(\vdash\) 1,90 |
3 |
Total |
40 |
Construção de uma distribuição de frequência¶
Para ilustrar como se constrói uma distribuição de frequência, vamos considerar um exemplo específico. Suponha que uma pesquisa foi feita e o seguinte conjunto de dados foi obtido:
Dados Brutos: 24-23-22-28-35-21-23-33-34-24-21-25-36-26-22-30-32-25-26-33-34-21-31-25-31-26-25-35-33-31.
dados = [24,23,22,28,35,21,23,33,34,24,21,25,36,26,22,30,32,25,26,33,34,21,31,25,31,26,25,35,33,31]
Rol de dados¶
A primeira coisa a fazer é ordenar os dados do menor para o maior, formando o rol de dados:
Rol de dados: 21-21-21-22-22-23-23-24-25-25-25-25-26-26-26-28-30-31-31-31-32-33-33-33-34-34-34-35-35-36.
np.sort(dados)
array([21, 21, 21, 22, 22, 23, 23, 24, 24, 25, 25, 25, 25, 26, 26, 26, 28,
30, 31, 31, 31, 32, 33, 33, 33, 34, 34, 35, 35, 36])
Amplitude total¶
Em seguida, calculamos a amplitude total \(R\) pela diferença entre o maior \(M\) e menor \(m\) valores obtidos na amostra.
Para o caso acima, \(R = 36-21 = 15\).
R = np.max(dados) - np.min(dados); R
15
Tamanho Amostral¶
Vamos calcular agora o tamanho amostral, ou seja, o número de observações obtidas na amostra.
n = len(dados); n
30
Para Series e DataFrames, podemos usar o método count() para retornar o tamanho amostral.
n = pd.Series(dados).count(); n
30
Distribuições e histogramas¶
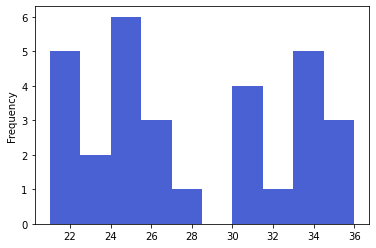
Para ter uma visão ampla sobre a distribuição de frequências para o nosso conjunto de dados, podemos plotar o histograma com plot.hist diretamente a partir da Series de dados.
d = pd.Series(dados);
d.plot.hist(color='#1b3ac9',alpha=0.8);
Número de classes e binning¶
A divisão das amostras em intervalos de classe pode ser chamada de binning. Bin é o termo utilizado para uma barra vertical no histograma. Por padrão, plot.hist usa 10 bins.
Há mais de uma forma de definir o número de (intervalos) de classe \(K\). A seguir, temos duas regras práticas de decisão:
Regra 1: \(K=5\), para \(n\leq 25\) e \(K \approx \sqrt{n}\), para \(n>25\).
Regra 2 (Fórmula de Sturges): \(K\approx 1 + 3,22\log n\).
Vamos aplicá-las aos nossos dados:
# binning usando np.ceil
def binning(d,rule='standard'):
if isinstance(d,list): d = np.array(d)
n = len(d)
if rule == 'standard':
if n <= 25: K = 5
else: K = int(np.ceil(np.sqrt(n)))
if rule == 'sturges':
K = int(np.ceil(1 + 3.22*np.log10(n)))
return K
K1,K2 = binning(dados,rule='standard'), binning(dados,rule='sturges');
K1,K2
(6, 6)
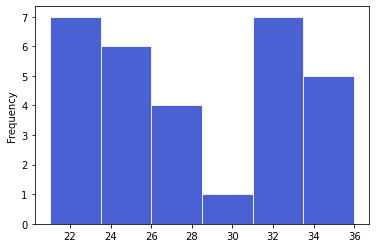
Uma vez que ambos os valores são iguais, podemos tomar \(K = K_1 = K_2 = 6\) e plotar o histograma especificando bins.
K = K1
d.plot.hist(bins=K,color='#1b3ac9',alpha=0.8,edgecolor='w');
Amplitude das classes¶
Para determinar o comprimento de cada intervalo, ou seja, a amplitude de cada classe \(h\), podemos adotar uma divisão uniforme, de modo que:
h = np.ceil(R/K); h
3.0
Limites das classes¶
Os limites das classes são estabelecidos da seguinte forma. Começando a partir do menor valor obtido da amostra, ou equivalentemente, o primeiro valor do rol de dados, somamos a amplitude de maneira progressiva. Dessa maneira, as seguintes classes serão obtidas.
Classes |
|---|
21 \(\vdash\) 24 |
24 \(\vdash\) 27 |
27 \(\vdash\) 30 |
30 \(\vdash\) 33 |
33 \(\vdash\) 36 |
36 \(\vdash\) 39 |
bin_ = [np.min(dados) + i*h.astype('int') for i in range(K+1)];
bin_
[21, 24, 27, 30, 33, 36, 39]
Frequência dos dados¶
Ao calcular a frequência de cada intervalo, a chamada frequência absoluta, montamos a seguinte tabela de distribuição de frequências será obtida.
Classes |
Frequência |
|---|---|
21 \(\vdash\) 24 |
7 |
24 \(\vdash\) 27 |
9 |
27 \(\vdash\) 30 |
1 |
30 \(\vdash\) 33 |
5 |
33 \(\vdash\) 36 |
7 |
36 \(\vdash\) 39 |
1 |
No pandas, a função cut cria classes a partir dos dados e o método value_counts() cria uma tabela de frequências.
T = pd.cut(dados, bins=bin_, right=False)
T
[[24, 27), [21, 24), [21, 24), [27, 30), [33, 36), ..., [24, 27), [24, 27), [33, 36), [33, 36), [30, 33)]
Length: 30
Categories (6, interval[int64]): [[21, 24) < [24, 27) < [27, 30) < [30, 33) < [33, 36) < [36, 39)]
# labels
T.codes
array([1, 0, 0, 2, 4, 0, 0, 4, 4, 1, 0, 1, 5, 1, 0, 3, 3, 1, 1, 4, 4, 0,
3, 1, 3, 1, 1, 4, 4, 3], dtype=int8)
# categorias
T.categories
IntervalIndex([[21, 24), [24, 27), [27, 30), [30, 33), [33, 36), [36, 39)],
closed='left',
dtype='interval[int64]')
# tabela de frequências
T.value_counts()
[21, 24) 7
[24, 27) 9
[27, 30) 1
[30, 33) 5
[33, 36) 7
[36, 39) 1
dtype: int64
Aplicações a testes aleatórios¶
# função genérica
def random_test(ns, dist='rand',binMethod='standard'):
if isinstance(ns,int): vals = '(' + str(ns) + ')'
elif isinstance(ns,tuple): vals = str(ns)
z = eval('np.random.' + dist + vals)
T = pd.cut(z,bins=binning(z,binMethod), right=False)
return pd.Series(z), T.value_counts()
Números randômicos
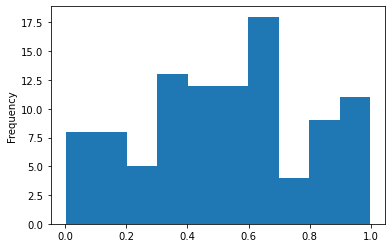
z1,T1 = random_test(100, dist='rand',binMethod='standard')
z1.plot.hist(); T1
[0.00228, 0.102) 8
[0.102, 0.201) 8
[0.201, 0.301) 5
[0.301, 0.4) 13
[0.4, 0.5) 12
[0.5, 0.599) 12
[0.599, 0.699) 18
[0.699, 0.798) 4
[0.798, 0.898) 9
[0.898, 0.998) 11
dtype: int64
z2,T2 = random_test(100, dist='rand',binMethod='sturges')
z2.plot.hist(); T2
[0.00262, 0.127) 19
[0.127, 0.251) 10
[0.251, 0.375) 13
[0.375, 0.499) 12
[0.499, 0.622) 10
[0.622, 0.746) 9
[0.746, 0.87) 14
[0.87, 0.995) 13
dtype: int64

Distribuição normal
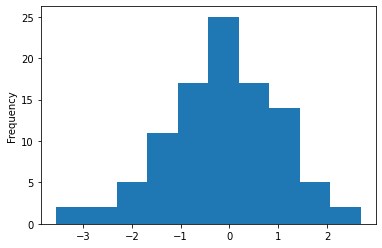
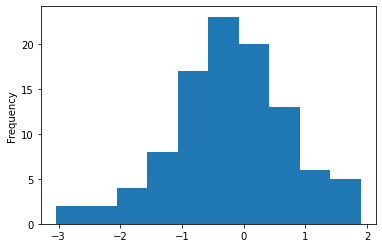
z3,T3 = random_test((0,1,100), dist='normal',binMethod='standard')
z3.plot.hist(); T3
[-3.549, -2.925) 2
[-2.925, -2.302) 2
[-2.302, -1.678) 5
[-1.678, -1.055) 11
[-1.055, -0.431) 17
[-0.431, 0.192) 25
[0.192, 0.816) 17
[0.816, 1.44) 14
[1.44, 2.063) 5
[2.063, 2.693) 2
dtype: int64
z4,T4 = random_test((0,1,100), dist='normal',binMethod='sturges')
z4.plot.hist(); T4
[-3.041, -2.424) 2
[-2.424, -1.808) 2
[-1.808, -1.191) 8
[-1.191, -0.574) 21
[-0.574, 0.0424) 30
[0.0424, 0.659) 20
[0.659, 1.276) 12
[1.276, 1.897) 5
dtype: int64
Medidas de Tendência Central¶
As medidas de tendência central (ou de centralidade) são as mais importantes de uma classe maior chamada de medidas de posição. Elas representam a tendência de concentração dos dados observados. A seguir, exploraremos algumas medidas de tendência central.
Média¶
Quantidade que tem por característica dar um “resumo” para o conjunto de dados. A média \(\overline{X}\) é obtida a partir de todos os elementos da distribuição e do tamanho da amostra.
Calculamos a média aritmética pela fórmula:
Para Series e DataFrames o método mean() retorna a média dos valores.
pd.Series(dados).mean()
27.833333333333332
Moda¶
Definimos a moda \(Mo\) de um conjunto de dados como o valor mais frequente deste conjunto.
Exemplos:
\(\{1, 2, 4, 5, 8\}\). Não há moda (amodal).
\(\{2, 2, 3, 7, 8\}\). Para esta amostra, \(Mo\) = 2 (unimodal).
\(\{1, 1, 10, 5, 5, 8, 7, 2\}\). Para esta amostra, \(Mo\) = 1 e \(Mo=\)5 (bimodal).
Para Series e DataFrames, o método mode() retorna a moda dos valores.
pd.Series(dados).mode()
0 25
dtype: int64
pd.Series([1,2,2,2,3,4,4,4,5]).mode()
0 2
1 4
dtype: int64
z4.mode()
0 -3.040819
1 -2.581601
2 -2.317073
3 -2.109276
4 -1.776528
...
95 1.489576
96 1.554068
97 1.774070
98 1.850478
99 1.892383
Length: 100, dtype: float64
Mediana¶
A mediana \(Md\) é o valor que divide o rol de dados em duas partes com a mesma quantidade de dados. O elemento mediano, \(E_{Md}\), é a posição no rol de dados onde a mediana está localizada.
Se o tamanho amostral \(n\) é ímpar, temos que \(E_{Md} = \frac{(n+1)}{2}\); se par, dois valores são possíveis, \(\frac{n}{2}\) e \(\frac{n}{2}+1\). No último caso, a mediana será a média dos valores assumidos nestas posições.
Exemplos:
\(\{1, 2, 4, 5, 8\}\). Como \(n\) é ímpar, \(E_{Md} = 3\), e \(Md = 4\).
\(\{2, 2, 4, 7, 8, 10\}\). Aqui, \(n\) é par. Assim, \(E_{Md,1} = \frac{6}{2} = 3\) e \(E_{Md,2} = \frac{6}{2}+1 = 4\). Daí \({Md} = \frac{4+7}{2} = 5,5\).
Para Series e DataFrames o método
median()retorna a mediana dos valores.
pd.Series(dados).median()
26.0
z2.median()
0.46822199470596426
Quantis e percentis¶
Quantis e percentis são utilizados para compreender os dados sob a perspectiva de “partes”. Por exemplo, dado o rol de dados \( d = \{x_i\}\) com \(n\) valores, procuramos pelo valor \(x_p\) que divide o rol em partes regulares. O valor \(x_p\) é o \(p\)-ésimo quantil, ou o \(100 \times p\)-ésimo percentil. Em particular, \(x_p = d[I_p]\), onde \(I_p\) é o índice (número inteiro) para o quantil no rol de dados.
Os seguintes nomes são usados na prática:
Percentis variam no intervalo 0 a 100.
Quartis variam no intervalo 0 a 4.
Quantis variam de qualquer valor para outro.
Entretanto, outras definições existem: os 3-quantis são chamados de tercis, os 5-quantis são chamados de quintis, os 12-quantis são chamados de duo-deciles, e assim por diante.
Uma tabela de correspondência útil para compreensão é a seguinte:
0-percentil = 0-quartil = menor valor do rol de dados
25-percentil = 1-quartil
50-percentil = 2-quartil = mediana
75-percentil = 3-quartil
100-percentil = 4-quartil = máximo valor do rol de dados
Como se vê, a mediana é o 50-percentil. Isto significa que ela representa o valor que está abaixo de 50% dos valores no rol de dados. Quantis, por sua vez, são uma generalização da mediana.
O código abaixo retorna o \(p\)-percentil de um rol de dados.
# 0 < p < 1
def quantil(d,p):
I_p = int(p*len(d))
return sorted(d)[I_p]
Por exemplo, para o nosso conjunto:
print(sorted(d),sep=',')
[21, 21, 21, 22, 22, 23, 23, 24, 24, 25, 25, 25, 25, 26, 26, 26, 28, 30, 31, 31, 31, 32, 33, 33, 33, 34, 34, 35, 35, 36]
quantil(d,0.0),quantil(d,0.25),quantil(d,0.5),quantil(d,0.75),quantil(d,0.9)
(21, 24, 26, 33, 35)
Comentário:
A mediana é o valor \(x_{1/2} = 26\). Ou seja, \(p= 1/2 = 0.5\). Isto equivale a dizer que a mediana é o \(1/2\)-quantil ou \(100 \times 1/2 = 50\)-percentil.
Para \(p=1/4\), temos o \(1/4\)-quantil ou \(100 \times 1/4 = 25\)-percentil. Este valor equivale a \(x_{1/4} = 24\).
24 é o primeiro quartil do rol, ou seja, 25% dos valores do rol são menores do que 24.
33 é o terceiro quartil do rol, ou seja, 75% dos valores do rol são menores do que 33.
Note
Para saber mais sobre a terminologia estatística “x-is”, veja a tabela do Apêndice A deste artigo de [Nicholas J. Cox].
O pandas possui a função quantile para calcular os quantis que desejarmos.
z1.quantile(0.22)
0.3232710053234671
# 1-, 2-, e 3-quartis
z4.quantile([0.25,0.5,0.75])
0.25 -0.881373
0.50 -0.237251
0.75 0.361105
dtype: float64
# 1-, 2- tercis
z2.quantile([0.33,0.66])
0.33 0.291451
0.66 0.633654
dtype: float64
Medidas de Dispersão¶
As medidas de dispersão medem o grau de variabilidade dos elementos de uma distribuição. O valor zero indica ausência de dispersão. As principais medidas de dispersão incluem: amplitude, desvio médio, variância e desvio padrão.
Como uma motivação para estudar as medidas de dispersão, consideremos a seguinte distribuição de notas é médias em uma classe.
Discente |
Notas |
Média |
||||
|---|---|---|---|---|---|---|
Antônio |
5 |
5 |
5 |
5 |
5 |
5 |
João |
6 |
4 |
5 |
4 |
6 |
5 |
José |
10 |
5 |
5 |
5 |
0 |
5 |
Pedro |
10 |
10 |
5 |
0 |
0 |
5 |
Observa-se que:
as notas de Antônio não variaram;
as notas de João variaram menos do que as notas de José;
as notas de Pedro variaram mais do que as notas dos demais;
Amplitude¶
A amplitude \(R\) fornece a maior variação possível dos dados. Ela é dada pela fórmula:
onde \(X_{max}\) é o valor máximo \(X_{min}\) o mínimo entre os dados.
Para Series e DataFrames os métodos max() e min() retornam respectivamente o máximo e o mínimo.
R = pd.Series(dados).max()-pd.Series(dados).min(); R
15
Desvio Médio¶
Para medir a dispersão dos dados em relação à média, é interessante analisar os desvios em torno da média, isto é, fazer a análise dos desvios:
Porém, a soma de todos os desvios é igual a zero, como podemos verificar com
Logo, será preciso encontrar uma maneira de se trabalhar com os desvios sem que a soma dê zero. Dessa forma, define-se o desvio médio \(DM\) pela fórmula:
Para Series e DataFrames o método mad() retorna a desvio médio dos valores.
pd.Series(dados).mad()
4.422222222222222
pd.Series(z3).mad()
0.8852462343234384
Observações:
A amplitude não mede bem a dispersão dos dados porque usam-se apenas os valores extremos em vez de todos os elementos da distribuição.
O desvio médio é mais vantajoso do que a amplitude, visto que leva em consideração todos os valores da distribuição e é menos sensível a outliers.
No entanto, o desvio médio não é tão frequentemente empregado no ajuste de modelos, pois não apresenta propriedades matemáticas interessantes. Porém é bastante utilizado na validação e comparação de modelos.
Note
“Um outlier é uma observação que se diferencia tanto das demais observações que levanta suspeitas de que aquela observação foi gerada por um mecanismo distinto” (Wikipedia, apud: Hawkins, 1980). Outlier é um dado que se distancia demasiadamente de todos os outros. Literalmente, o “ponto fora da curva”.
Variância¶
A variância \(\sigma^2\) é a medida de dispersão mais utilizada. Ela é dada pelo quociente entre a soma dos quadrados dos desvios e o número de elementos, cuja fórmula é dada por:
onde \(\sigma^2\) indica a variância populacional (lê-se “sigma ao quadrado” ou “sigma dois”). Neste caso, \(\overline{X}\) e \(N\) na formúla representam a média populacional e o tamanho populacional, respectivamente.
Variância Amostral¶
Temos a seguinte definição de variância amostral:
Para Series e DataFrames o método var() retorna a variância amostral dos valores.
pd.Series(dados).var()
24.281609195402304
pd.Series(z3).var()
1.3151695546082973
Desvio Padrão¶
Temos também outra medida de dispersão, que é a raiz quadrada da variância, chamada de desvio padrão. Assim,
é o desvio desvio padrão populacional, e
é o desvio desvio padrão amostral.
Para o cálculo do desvio padrão, deve-se, primeiramente, determinar o valor da variância e, em seguida, extrair a raiz quadrada desse resultado.
Para Series e DataFrames o método std() retorna o desvio padrão dos valores.
pd.Series(dados).std()
4.9276372832628725
np.sqrt(pd.Series(dados).var())
4.9276372832628725
pd.Series(z3).std()
1.146808421057457
np.sqrt(pd.Series(z3).var())
1.146808421057457
Resumo Estatístico de uma Series ou DataFrame¶
Para obtermos um resumo estatístico de uma Series ou DataFrame do pandas, utilizamos o método describe. O método describe exclui observações ausentes por padrão.
Exemplos:
pd.Series(dados).describe()
count 30.000000
mean 27.833333
std 4.927637
min 21.000000
25% 24.000000
50% 26.000000
75% 32.750000
max 36.000000
dtype: float64
pd.DataFrame(z2).describe()
| 0 | |
|---|---|
| count | 100.000000 |
| mean | 0.472693 |
| std | 0.307344 |
| min | 0.002618 |
| 25% | 0.200659 |
| 50% | 0.468222 |
| 75% | 0.755517 |
| max | 0.994382 |
Observações
Se as entradas da Series não forem numéricas, o método
describeretornará uma tabela contendo as quantidades de valores únicos, o valor mais frequente e a quantidade de elementos do valor mais frequente.No caso de um DataFrame que contenha colunas numéricas e colunas não-numéricas, o método
describeirá considerar apenas as colunas numéricas.
Exemplos:
serie_ex1 = pd.Series(['a','b','c','d','e','f','g','h','i','j'])
serie_ex2 = pd.Series(range(10))
serie_ex1.describe()
count 10
unique 10
top j
freq 1
dtype: object
serie_ex2.describe()
count 10.00000
mean 4.50000
std 3.02765
min 0.00000
25% 2.25000
50% 4.50000
75% 6.75000
max 9.00000
dtype: float64
Exemplo:
df_exemplo = pd.concat([serie_ex1, serie_ex2], axis=1)
df_exemplo
| 0 | 1 | |
|---|---|---|
| 0 | a | 0 |
| 1 | b | 1 |
| 2 | c | 2 |
| 3 | d | 3 |
| 4 | e | 4 |
| 5 | f | 5 |
| 6 | g | 6 |
| 7 | h | 7 |
| 8 | i | 8 |
| 9 | j | 9 |
Exemplo:
df_exemplo.describe()
| 1 | |
|---|---|
| count | 10.00000 |
| mean | 4.50000 |
| std | 3.02765 |
| min | 0.00000 |
| 25% | 2.25000 |
| 50% | 4.50000 |
| 75% | 6.75000 |
| max | 9.00000 |
Hint
É possível controlar o que será considerado em describe utilizando os argumentos include ou exclude. No caso, devemos passar uma lista contendo os parâmetros a serem incluídos ou excluídos como argumento. Para uma lista dos parâmetros disponíveis, consulte a documentação da função select_dtypes().
Exemplos:
df_exemplo.describe(exclude='number')
| 0 | |
|---|---|
| count | 10 |
| unique | 10 |
| top | j |
| freq | 1 |
df_exemplo.describe(include='object')
| 0 | |
|---|---|
| count | 10 |
| unique | 10 |
| top | j |
| freq | 1 |
Exemplo:
df_exemplo.describe(include='all')
| 0 | 1 | |
|---|---|---|
| count | 10 | 10.00000 |
| unique | 10 | NaN |
| top | j | NaN |
| freq | 1 | NaN |
| mean | NaN | 4.50000 |
| std | NaN | 3.02765 |
| min | NaN | 0.00000 |
| 25% | NaN | 2.25000 |
| 50% | NaN | 4.50000 |
| 75% | NaN | 6.75000 |
| max | NaN | 9.00000 |
