.ipynb .pdf

Binder Colab Live Code

Contents

Aprendizado de máquina - II

No capítulo anterior, aprendemos a resolver um problema de classificação, que recai na classe de aprendizado de máquina supervisionado. Neste capítulo, estudaremos o aprendizado de máquina não supervisionado resolvendo um problema de clusterização.

Como já sabemos, no aprendizado não supervisionado, procuramos por “estruturas escondidas” em um banco de dados não rotulado. Enquanto no aprendizado supervisionado é possível medir erros entre os valores esperados e os previstos, no aprendizado não supervisionado os algoritmos devem apelar para as exclusivamente para as features do banco de dados e categorizá-las aplicando algum critério estatístico ou geométrico.

Breves comentários sobre aprendizagem

A aprendizagem é um conceito que pode ser quantificado por meio de erros. Durante o treinamento de um algoritmo de machine learning, dois erros são estimados.

O primeiro é o erro de treinamento, que mede a discrepância entre as amostras observadas e as amostras apenas do conjunto de treinamento. No problema de classificação por exemplo, o erro de treinamento \(e_i = e(x_i,y_i)\) para cada observação \(x_i\) e resposta \(y_i\) poderia ser calculado usando uma função indicadora que contaria todas as amostras corretamente calculadas. Ou seja,

\[\begin{split}e_i = e(x_i,y_i) = \begin{cases} 1, \ \ \text{se} \ \ h(x_i) = y_i \\ 0, \ \ \text{caso contrário} \end{cases}\end{split}\]

O erro de treinamento seria então definido por

\[E_{tr} = \frac{ \sum_{i=1}^n e_i }{n},\]

para \(n\) amostras do conjunto de treinamento.

O segundo erro é o erro de teste ou erro de generalização, que é um erro médio calculado sobre os dados não vistos. Este erro é chamado de \(E_gen\).

Em geral, \(E_{gen} \geq E_{tr}\) e a aprendizagem é atingida quando \(E_{gen}\) é o menor possível. Para tanto, intuitivamente, ou \(E_{tr}\) deve tender a zero, ou \(E_{gen}\) deve ser aproximar de \(E_{tr}\).

Assim, a aprendizagem é o resultado de \(E_{tr} \to 0\), ou \(E_{gen} \approx E_{tr}\). Isto é, um excelente treinamento deve conduzir a um modelo de aprendizagem robusto.

A aprendizagem é medida por meio de curvas de aprendizagem, que possuem aparência assintótica. Modelos com alto desempenho durante a etapa de treinamento que generalizam mal tendem a sofrer um superajustamento (overfitting). Modelos com baixo desempenho já durante a etapa de treinamento tendem a sofrer um subajustamento (underfitting). Ambos os comportamentos são percebidos nas curvas de aprendizagem. A correção de overfitting ou underfitting pode ser feita com várias técnicas. Uma delas é a regularização.

Treinamento, validação e generalização

Vale fazer um breve adendo sobre esses três conceitos:

• treinamento: etapa em que se verifica o desempenho de um modelo a partir de uma classe de modelos.

• validação: etapa em que se selecionam os melhores hiperparâmetros do modelo tendo por base estimativas do erro de generalização.

• generalização (ou teste): etapa exclusiva em que se avalia o desempenho final do modelo sobre um conjunto de dados que nunca deve ser usado nas etapas de treinamento ou validação.

O ajustamento dos melhores parâmetros duranta a etapa de validação pode ser realizado por várias técnicas. Uma das mais conhecidas é a validação cruzada (cross validation).

Estudo de caso: clusterização de dados aleatórios

Estudaremos um problema de clusterização como exemplo de aplicação do aprendizado de máquina não supervisionado. Relembre que nesta classe de aprendizado, não há como mensurar erros no cálculo de desempenho do modelo, visto que os dados fornecidos não são rotulados. Então, a única maneira de explicar os dados dá-se por critérios estatísticos, geométricos ou de similaridade.

O que é clusterização?

A clusterização é baseada no particionamento dos dados não rotulados em subconjuntos disjuntos chamados clusters, de forma que os elementos de um cluster sejam altamente similares (alta similaridade intra-classe) e os elementos de clusters distintos possuam baixa similaridade com os os demais clusters (baixa similaridade inter-classe ).

Devido à arbitrariedade com que os dados podem ser agrupados em clusters, a clusterização tende a ser subjetiva e a qualidade dependente da aplicação e da avaliação do analista.

Similaridade e distância

Estabelecer “similaridade” entre instâncias pode ser um pouco difícil. Em problemas de clusterização, uma forma de aproximar essa ideia é usar distâncias. Uma fórmula generalizada é a distância de Minkowski, dada por

\[d({\bf x},{\bf y}) = \left( \sum_{i=1}^d | x_i - y_i |^p \right)^{1/p},\]

com \({\bf x}\) e \({\bf y}\) vetores do espaço \(\mathbb{R}^n\) e \(p \in \mathbb{R}\) é um parâmetro. Dependendo do valor de \(p\), a fórmula se reduz a outras distâncias conhecidas:

• Se \(p = 2\), temos a distância Euclidiana;

• Se \(p = 1\), temos a distância de Manhattan (ou distância do taxista);

• Se \(p = \infty\), temos a distância de Chebyshev (ou distância do máximo), definida por \(\max \{ | x_i - y_i | \}\), isto é, a componente com o maior módulo.

Hint

Para saber mais sobre outras definições de distância, veja a documentação da função scipy.spatial.distance do módulo Scipy.

O algoritmo k-means

k-means é um algoritmo classificado como de partição rígida que atribui cada elemento no espaço de features a um único cluster. Os passos do algoritmo são:

1. Inicialize o valor k de clusters desejados;

2. Inicialize os centroides dos k clusters;

3. Atribua cada uma das n amostras de dados ao cluster cujo centroide está mais próximo da amostra;

4. Redefina os k centroides iterativamente assumindo que estejam corretos;

5. Se nenhuma amostra migrar de um cluster para outro na última iteração, pare. Caso contrário, retorne ao passo 3.

Vejamos um exemplo sobre um conjunto de dados aleatórios.

import numpy as np
import matplotlib.pylab as plt

# cria dados aleatórios
N = 40

X1 = 1.25*np.random.randn(N,2)
X2 = 5 + 1.5*np.random.randn(N,2)
X3 = [8,3] + 1.2*np.random.randn(N,2)

X = np.concatenate([X1,X2,X3])

X.shape

(120, 2)

Vamos criar rótulos para os 3 grupos e mostrar a clusterização segundo o que nós pré-determinamos e o que, de fato, é passado como entrada para o algoritmo.

# cria labels
c = np.concatenate([np.full(N,1), np.full(N,2), np.full(N,3)])

plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.scatter(X1[:,0],X1[:,1],color='r')
plt.scatter(X2[:,0],X2[:,1],color='g')
plt.scatter(X3[:,0],X3[:,1],color='b')
plt.title('Dados rotulados')

plt.subplot(1,2,2)
plt.scatter(X[:,0],X[:,1],color='k')
plt.title('Dados "vistos" pelo algoritmo');

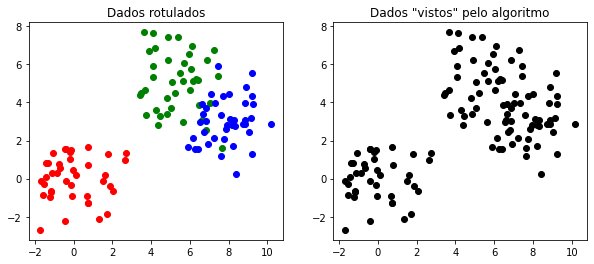
Usa k-means com inicialização de 3 clusters.

from sklearn import cluster

# no. de clusters
k = 3

# ajusta parâmetros de aprendizagem
cfit = cluster.KMeans(init='random',n_clusters=k)
cfit.fit(X)

KMeans(init='random', n_clusters=3)

# labels do ajuste
print(cfit.labels_)

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 1 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1
 1 1 2 1 2 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2]

# plota comparativo de labels (original x ajuste)
cl = cfit.labels_ + 1

plt.scatter(X[cl==1,0], X[cl==1,1],color='r')
plt.scatter(X1[:,0],X1[:,1],color='gray',edgecolor='k',alpha=0.4)

plt.scatter(X[cl==2,0], X[cl==2,1],color='g')
plt.scatter(X2[:,0],X2[:,1],color='gray',edgecolor='c',alpha=0.4)

plt.scatter(X[cl==3,0], X[cl==3,1],color='r')
plt.scatter(X3[:,0],X3[:,1],color='gray',edgecolor='m',alpha=0.4);

plt.title('Rótulos originais x rótulos do ajuste');

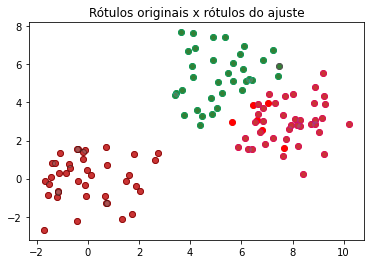
Criando pontos novos no espaço que cobre os dados originais.

# gera "grade" 2D de pontos 
# em [-5,15] x [-5,15]
x = np.linspace(-5,15,200)
XX,YY = np.meshgrid(x,x)
sz = XX.shape

# concatena
data = np.c_[XX.flatten(), YY.flatten()]

# predição
Z = cfit.predict(data)

Verificando partição do espaço determinado pelo algoritmo x dados originais.

# partições do espaço
plt.imshow(Z.reshape(sz), interpolation='bilinear', 
           origin='lower', extent=(-5,15,-5,15), 
           alpha=0.3,vmin=0,vmax=k-1)


plt.scatter(X[c==1,0], X[c==1,1],color='r')
plt.scatter(X[c==2,0], X[c==2,1],color='g')
plt.scatter(X[c==3,0], X[c==3,1],color='b')
plt.title('Partições do espaço');

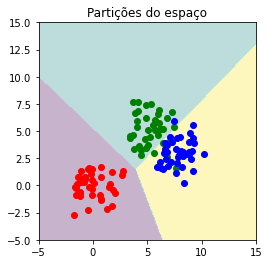
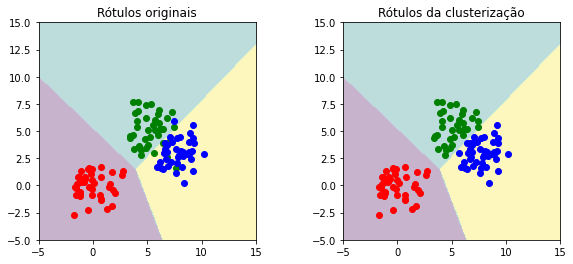
Então, comparamos o resultado da clusterização em comparação com os dados originais.

plt.figure(figsize=(10,4))

plt.subplot(1,2,1)

# overlay
plt.imshow(Z.reshape(sz), interpolation='bilinear', 
           origin='lower', extent=(-5,15,-5,15), 
           alpha=0.3,vmin=0,vmax=k-1)

# original
plt.title('Rótulos originais')
plt.scatter(X[c==1,0], X[c==1,1],color='r')
plt.scatter(X[c==2,0], X[c==2,1],color='g')
plt.scatter(X[c==3,0], X[c==3,1],color='b')

plt.subplot(1,2,2)

# overlay
plt.imshow(Z.reshape(sz), interpolation='bilinear', 
           origin='lower', extent=(-5,15,-5,15), 
           alpha=0.3,vmin=0,vmax=k-1)

# clusterização
plt.title('Rótulos da clusterização')
plt.scatter(X[cl==1,0], X[cl==1,1],color='r')
plt.scatter(X[cl==2,0], X[cl==2,1],color='g')
plt.scatter(X[cl==3,0], X[cl==3,1],color='b');

Métricas de qualidade para clusterização

Vejamos brevemente uma métrica conhecida para comparar resultados de clusterização.

Coeficiente de Silhueta

O coeficiente de silhueta \(s\) é um valor atribuído a cada ponto de um cluster para medir a “silhueta” de seu cluster. Em linhas gerais, este coeficiente é usado para definir se houve uma “boa” clusterização do dataset. Matematicamente,

\[s(i) = \frac{b(i) - a(i)}{\max \{a(i),b(i)\}},\]

onde

• \(a(i)\) é a distância média intra-cluster da amostra \(i\), isto é, a distância média da amostra \(i\) a todos as suas “irmãs”, percententes ao seu mesmo cluster. Este valor mede a dissimilaridade de \(i\) em relação às suas amostras “irmãs”.

• \(b(i)\) é a distância média inter-cluster da amostra \(i\), considerando o cluster A ao qual ela pertence e o cluster B mais próximo de A. Este valor mede a dissimilaridade de \(i\) em relação a todas as amostras em B.

O valor de \(s\) varia no intervalo [-1,1] e a interpretação é a seguinte. Quando \(s=-1\), a clusterização é considerada incorreta; quando \(s=1\), a clusterização está muito densa. Quando \(s \approx 0\), há clusters que sobrepõem.

Vamos calcular \(s\) para o nosso exemplo.

from sklearn import metrics

ss = metrics.silhouette_samples(X,cl,metric='euclidean')

ssm = metrics.silhouette_score(X,cl,metric='euclidean')

plt.title('Coeficiente de silhueta por amostra')
plt.plot(ss,'+');
plt.plot(np.arange(len(ss)),np.full(np.shape(ss),ssm),':',label='s médio');
plt.legend();

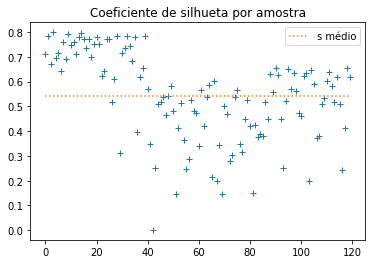
Análise de silhueta

O plot de silhueta permite que busquemos o número adequado de clusters a partir de uma análise gráfica dos valores de \(s\). Em outras palavras, a análise de silhueta é usada para escolher um valor ótimo para o número de clusters a serem determinados.

import matplotlib.cm as cm

fig, (ax1,ax2) = plt.subplots(1,2)
fig.set_size_inches(8, 4)

ax1.set_xlim([-0.2,1])
ax1.set_ylim([0, len(X) + (k + 1) * 10])


y_lower = 10
for i in range(1,k+1):
    ssi = ss[cl == i] # i-th cluster s
    ssi.sort()
    sizei = ssi.shape[0]
    y_upper = y_lower + sizei
    
    color = cm.nipy_spectral(float(i) / k)
    ax1.fill_betweenx(np.arange(y_lower, y_upper),0,
                      ssi,facecolor=color, edgecolor=color,
                      alpha=0.7)
    ax1.text(-0.05, y_lower + 0.5 * sizei, str(i))
    y_lower = y_upper + 10
    
ax1.set_title(f'Plot de silhueta: {k} clusters')
ax1.set_xlabel("s")
ax1.set_ylabel("Rótulos dos clusters")    
    
ax1.axvline(x=ssm, color="red", linestyle="--")
    
colors = cm.nipy_spectral(cl.astype(float)/k)
ax2.scatter(X[:, 0],X[:, 1],marker='o', s=30, lw=0, alpha=1.0,
            c=colors, edgecolor='k')    
centroides = cfit.cluster_centers_
ax2.scatter(centroides[:, 0], centroides[:, 1], marker='o',
            c="white", alpha=1, s=200, edgecolor='k')

for i, c in enumerate(centroides):
    
    ax2.scatter(c[0], c[1], marker=f'$%d$' % (i+1), alpha=1,
                s=50, edgecolor='k')
    
ax2.set_title("Clusters") 
ax2.set_xlabel("Feature #1")
ax2.set_ylabel("Feature #2")
plt.suptitle(("Análise de silhueta por k-means: %d clusters" % k),
                 fontsize=12, fontweight='bold');

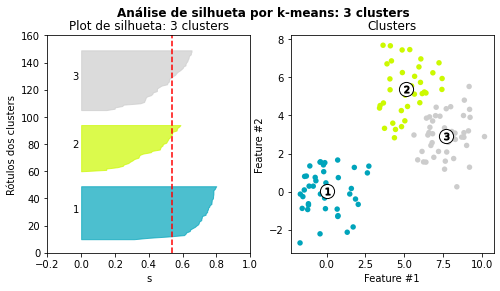
A análise de silhueta mostra que 3 clusters é um número adequado porque em todos eles há amostras com valor de \(s\) acima da média. A espessura das silhuetas também ajuda a ter uma ideia do “tamanho” dos clusters.

Aprendizado de máquina - I Otimização