Questionário 25 (Q25)

Orientações:

  • Registre suas respostas no questionário de mesmo nome no SIGAA.

  • O tempo de registro das respostas no questionário será de 10 minutos. Portanto, resolva primeiro as questões e depois registre-as.

  • Haverá apenas 1 (uma) tentativa de resposta.

  • Submeta seu arquivo-fonte (utilizado para resolver as questões) em formato .ipynb pelo SIGAA anexando-o à Tarefa denominada “Envio de arquivo” correspondente ao questionário.

Nota: o arquivo-fonte será utilizado apenas como prova de execução da tarefa. Nenhuma avaliação será feita quanto ao estilo de programação.

Em sua forma completa, o fragmento de código abaixo produz a seguinte plotagem para uma família de funções \(g(x;k)\) a um parâmetro \(k\) através do módulo matplotlib. Reconstitua as partes ausentes do código para reproduzir o mesmo gráfico e responda às questões 1 e 2 a seguir.

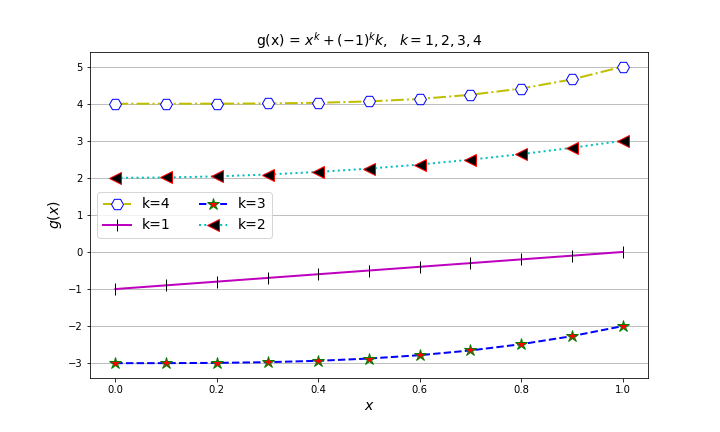
../_images/g-plots.png

Fig. 14 Família de funções g(x;k).

import matplotlib.pyplot as plt
from numpy import linspace

M = (A, '-', '|', E, 'k', 1, 12, 2)
N = ('c', ':', H, 'k', C, 1, 12, 2)
O = (G, '--', B, 'r', 'g', 1, 12, 2)
P = ('y', D,  'H', 'w', F, 1, 12, 2)        

d = dict(zip([4,1,3,2],(P,M,O,N)))

def p(a,b,n,k,opt):      
    keys = ('c','ls','marker','mfc','mec','mew','ms','lw')
    d = dict(zip(keys,opt))
    x = linspace(a,b,n)
    g = lambda x,k: x**k + (-1)**k*k
    plt.plot(x, g(x,k), label=f'k={k}',**d)
             
plt.figure(figsize=(10,6))        
for k,opt in d.items():
    p(K,I,J,k,opt)
    
plt.legend(loc='center left', ncol=2,fontsize=14)
plt.xlabel('$x$',fontsize=14); plt.ylabel('$g(x)$',fontsize=14)
plt.title('g(x) = $x^k + (-1)^kk, \ \ k = 1,2,3,4$',fontsize=14);
plt.grid(axis='y')

Questão 1: Marque a alternativa que contém os valores corretos para as variáveis A, B, C, … , H, nesta ordem.

A. '*', 's', '-.', 'k', '+', 'b', 'a', '<'

B. '#fefefe', '*', 'r', ':', 'b', 'k', 'g', '<'

C. 'g, 's', 'y', '-.', 'k', '(', 'c', 'v'

D. 'm', '*', 'r', '-.', 'y', 'b', 'b', '<'

Questão 2: Marque a alternativa correta:

A. I, J, K = 1., 10, 0.

B. I, J, K = 0., 10.0, 11.

C. I, J, K = 1., 11, 0.

D. I, J, K = -1., 1, 10

Questão 3: A energia cinética \(K\) de uma partícula de massa \(m\) que se move com velocidade dada por um vetor \(\vec{v}\) pode ser calculada como:

\[K = m\dfrac{\langle \vec{v}, \vec{v}\rangle}{2}.\]

Determine a variação de energia cinética \(\Delta K = K_B - K_A\) de uma partícula de pó químico que se moveu do ponto A para o ponto B sabendo que sua massa é de 0.004 kg e que a sua velocidade em A e em B, eram, respectivamente, dadas pelos vetores:

\[\begin{split}\vec{v}_A = 10\vec{i} - 2.5\vec{j} + 0.5\vec{k} \\ \vec{v}_B = 2.5\vec{i} -1.1\vec{j} + 0\vec{k}\end{split}\]

Calcule a norma Euclidiana aproximada \(V_B\) de \(\vec{v}_B\) e assinale a alternativa correta:

A. \(V_B \approx 2.731\), \(\Delta K < 0\)

B. \(V_B \approx 3.123\), \(\Delta K < 0\)

C. \(V_B \approx 3.123\), \(\Delta K > 0\)

D. \(V_B \approx -1.210\), \(\Delta K > 0\)

Questionário 24 (Q24) Questionário 31 (Q31)