Laboratório 5

Resolva todos os problemas por computação.

Problema 1: Considere os seguintes vetores:

\[\begin{split}\vec{u} = 4\vec{i} + 3\vec{j} + 2\vec{k} \\ \vec{v} = 1\vec{i} + 3\vec{j} + 1\vec{k} \\ \vec{w} = 2\vec{i} + 1\vec{j} + 3\vec{k}\end{split}\]

Calcule as seguintes operações de álgebra linear:

a) \(\vec{u} + \vec{v}\)

b) \(\vec{u} + \vec{v} - \vec{w}\)

c) \(\alpha\vec{u} + \beta\vec{v}\), para \(\alpha = 0.5,\sqrt{3},1.5\) e \(\beta = e,2,-5\)

d) \(\langle \vec{u}, \vec{v} \rangle\) (produto interno)

e) \(\langle \vec{u} - \vec{v}, \vec{v} + \vec{w} \rangle\)

f) \(\theta(5\vec{v},-2\vec{w})\) (ângulo entre dois vetores)

Problema 2: Matrizes podem ser criadas a partir da organização de vetores alinhados em forma de colunas. Por exemplo, se \(\vec{x} = \vec{i} + 2\vec{j}\) e \(\vec{y} = -\vec{i}-2\vec{j}\), então a matriz \(A = [\vec{x} \ \ \vec{y}]\) é dada por

\[\begin{split}A = \begin{bmatrix} 1 & -1 \\ 2 & 2 \end{bmatrix}\end{split}\]

A partir dos vetores definidos no Problema 1, definamos as seguintes matrizes:

\[\begin{split}B = [\vec{u} \ \ \vec{v}] \\ C = [\vec{v} \ \ \vec{w}] \\ D = [\vec{u} \ \ \vec{v} \ \ \vec{w}] \\ E = [\vec{z} \ \ \vec{t}], \ \ \vec{z} = \vec{u} + \vec{v}, \vec{t} = 2\vec{w} \\ F = [-\vec{z} \ \ -\vec{t} \ \ \vec{w}]^T, \ \ \vec{z} = \vec{u} - \vec{v}, \vec{t} = 1/2\vec{v}, \end{split}\]

onde \(^{T}\) é o símbolo para de transposição.

Calcule:

a) \(B + C\)

b) \(2B - C\)

c) \(B^T - C^T\)

d) \(BC^T\) (produto de matrizes)

e) \((B + C)^2\), (note que para uma matriz \(A\), \(A^2 = AA\))

f) \(B^T\vec{v}\) (produto matriz vetor)

g) \(D - EE^T\)

h) \(D + 2EE^T - F\)

i) \(D\vec{u} - F\vec{w}\)

Problema 3: A energia cinética \(K\) de uma partícula de massa \(m\) que se move com velocidade dada por um vetor \(\vec{v}\) pode ser calculada como:

\[K = m\dfrac{\langle \vec{v}, \vec{v}\rangle}{2}.\]

Determine a variação de energia cinética \(\Delta K = K_B - K_A\) de uma partícula de pó químico que se moveu do ponto A para o ponto B sabendo que sua massa é de 0.004 kg e que a sua velocidade em A e em B, eram, respectivamente, dadas pelos vetores:

\[\begin{split}\vec{v}_A = 10\vec{i} - 2.5\vec{j} + 0.5\vec{k} \\ \vec{v}_B = 2.5\vec{i} -1.1\vec{j} + 0\vec{k}\end{split}\]

Verifique se \(\Delta K \ge 0\) ou \(\Delta K < 0\).

Problema 4: Considere a função chapeu (hat), definida por

\[\begin{split} H(x) = \begin{cases} 0,& x < 0\\ x,& 0 \le x < 1\\ 2-x,& 1 \le x \le 2\\ 0,& x \ge 2 \end{cases}.\end{split}\]

no domínio \([-1,3]\).

Tarefas:

  • plote o gráfico da função \(H(x)\) (gráfico 1);

  • plote o gráfico da função \(1 - H(x)\) na mesma figura (gráfico 2);

Para o gráfico 1, use a seguinte formatação:

  • 50 valores para domínio e imagem;

  • tipo de linha: espessa;

  • cor de linha: vermelha;

  • espessura de linha: 2pt

  • texto de legenda: “H(x)”

Para o gráfico 2, use a seguinte formatação:

  • 80 valores para domínio e imagem;

  • tipo de linha: nenhum;

  • tipo de marcador: circular;

  • cor de face do marcador: branca;

  • cor de aresta do marcador: preta;

  • texto de legenda: “1 - H(x)”

Para ambos

  • adicione gradeado apenas horizontal

  • posição de legenda: central à direita;

  • texto do eixo x: “domínio”

  • texto do eixo y: “imagem”

  • título: “função chapeu / invertida”

Você deve gerar um gráfico como o da figura abaixo.

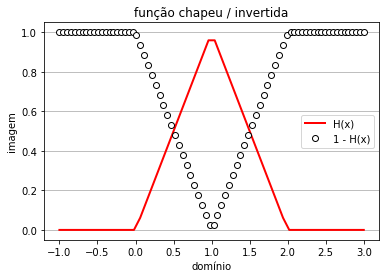
_images/hat.png

Fig. 3 Gráficos das funções chapeu e chapeu invertida no domínio [-1,3].

Observação: para uma solução completamente vetorizada, as funções where e logical_and do numpy podem ser úteis.

Laboratório 4 Lista de exercícios 1