Laboratório 1

Resolva todos os problemas por computação.

Problema 1: Calcule a hipotenusa \(c\) para um triângulo retângulo com catetos medindo \(a = \frac{e^{1.2}}{\pi}\sqrt{111.4}\) e \(b = 4!\textrm{sen}(65\pi/51 + 210)\).

Problema 2: A fórmula de Heron para calcular a área de um triângulo qualquer com lados medindo \(x_1\), \(x_2\) e \(x_3\) é dada por \(A = \sqrt{p(p - x_1)(p - x_2)(p - x_3)}\), onde \(p\) é o semiperímetro do triângulo. Assumindo que \(x_1=a\), \(x_2=b\) e \(x_3=c\), para \(a\), \(b\) e \(c\) encontrados pelo Problema 1, calcule \(A\).

Problema 3: Suponha que \(b\) seja a altura do triângulo retângulo do Problema 1. Calcule a área \(A_2\) do triângulo retângulo pela fórmula tradicional. Qual é o valor de \(|A - A_2|\), sendo \(A\) o valor obtido no Problema 2.

Problema 4: A tampa superior do farol do automóvel Mercedes-Benz 203 series C-Class Sports Coupés pode ser modelada aproximadamente pela união de duas elipses \(E_1\) e \(E_2\), centradas em \(C_1\) e \(C_2\), respectivamente, excluindo-se uma vez a área hachurada que se obtém pela intersecção (superposição) das duas elipses (vide figura abaixo). O arco entre os pontos \(P\) e \(Q\) da elipse \(E_1\) (cor vermelha) possui comprimento \(d_1 = 9.45 \, cm\), enquanto que o segundo arco (cor azul) entre os mesmos pontos, pertencente à elipse \(E_2\), possui comprimento \(d_2 = 10.25 \, cm\).

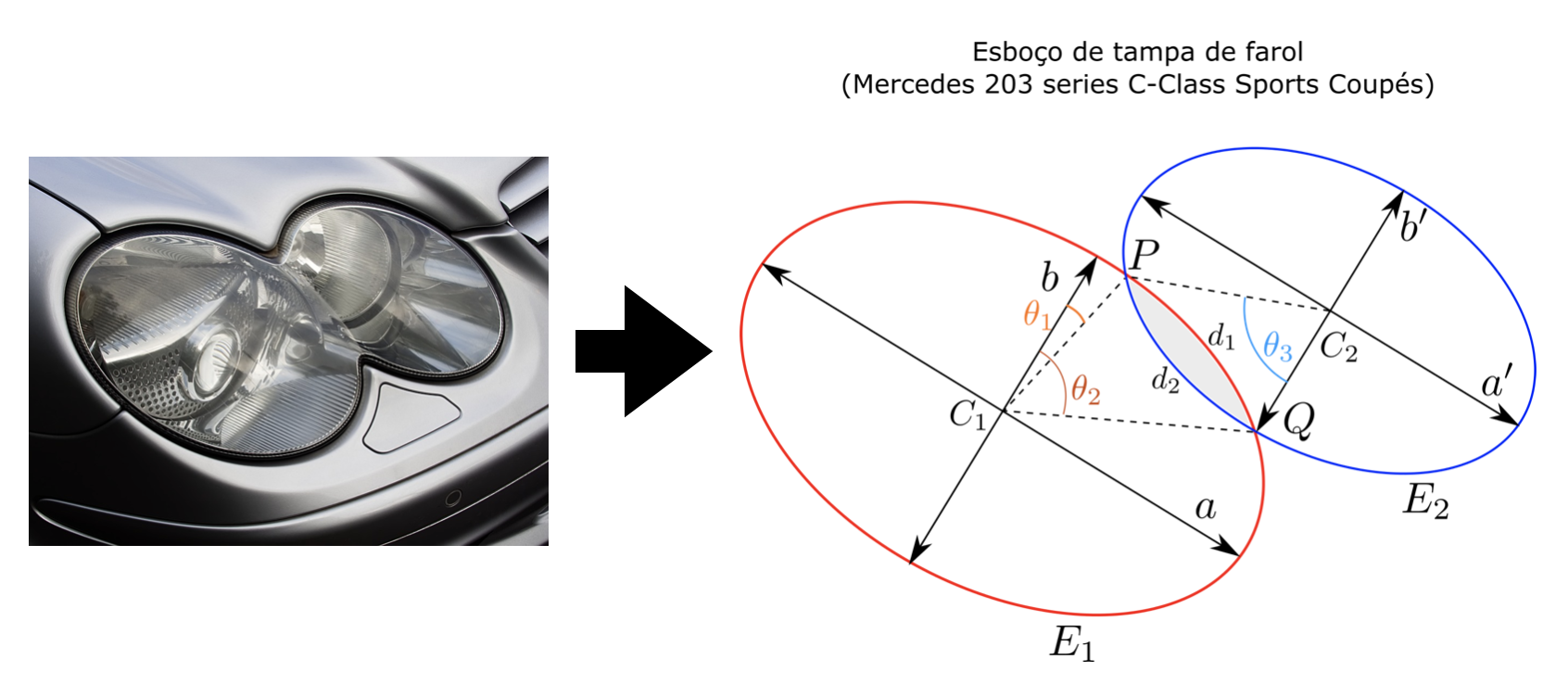
_images/farol-mercedes.png

Fig. 1 Modelo de farol do Mercedes-Benz 203 series C-Class.

Na época em que este carro foi desenvolvido, a Engenharia de Produtos da Mercedes-Benz precisou estimar o custo com vedação das tampas dos faróis para previsão orçamentária. Suponha que o comprimento da borracha de vedação de cada tampa de farol foi calculado como a soma dos perímetros de \(E_1\) e \(E_2\) subtraindo-se disso a soma \(d_1 + d_2\). Com o custo da borracha a 0,75 centavos de dólar por centímetro, calcule o valor aproximado, em reais, que a Mercedes despendeu apenas com borrachas de vedação para os faróis desse modelo para produzir 2000 automóveis. Use a taxa de câmbio 1 dólar : 2.35 reais.

Dados:

  • Segunda aproximação de Ramanujan para calcular o perímetro de uma elipse com semi-eixos maior \(a\) e menor \(b\):

\[p_e = \pi(a + b)\Bigg(1 + \frac{3h}{10 + (4 - 3h)^{1/2}}\Bigg), \ \ h = \frac{(a - b)^2}{(a + b)^2}\]

  • a = 12.5 cm (comprimento do semi-eixo maior de \(E_1\))

  • b = 0.39a (comprimento do semi-eixo menor de \(E_1\))

  • a' = 0.79a (comprimento do semi-eixo maior de \(E_2\))

  • b' = 0.31a (comprimento do semi-eixo menor de \(E_2\))

8. Leitura e Escrita de Arquivos de Planilha Laboratório 2