Laboratório 4

Resolva todos os problemas por computação.

Problema 1: O Índice de Massa Corpórea (IMC) é usado para saber se um indivíduo está no peso ideal. Ele é definido pela fórmula

\[IMC = \dfrac{M}{A^2},\]

onde \(M\) é a massa (considere quilogramas) do indivíduo e \(A\) é a sua altura (considere metros). Um indíviduo tem peso normal se seu IMC estiver no intervalo faixa \(18.5 \leq IMC < 25.0\).

A seleção brasileira masculina de futebol profissional convocada para a Copa do Mundo 2018 era composta de 23 jogadores, a saber: Alisson, Casemiro, Cássio, Danilo, Douglas Costa, Ederson, Fagner, Fernandinho, Filipe Luis, Firmino, Fred, Gabriel Jesus, Geromel, Marcelo, Marquinhos, Miranda, Neymar, Paulinho, Philippe Coutinho, Renato Augusto, Taison, Thiago Silva e Willian.

O arquivo copa2018.npy, disponibilizado juntamente com este arquivo, contém uma tabela de peso, altura e idade de cada um desses atletas.

O gráfico abaixo plota o valor do IMC para cada um desses jogadores. Todos os jogadores possuem peso ideal, mas a linha tracejada divide-os em dois grupos:

  • Grupo 1: aqueles na faixa ideal cujo IMC é menor do que 21.7.

  • Grupo 2: aqueles na faixa ideal cujo IMC é maior do que 21.7.

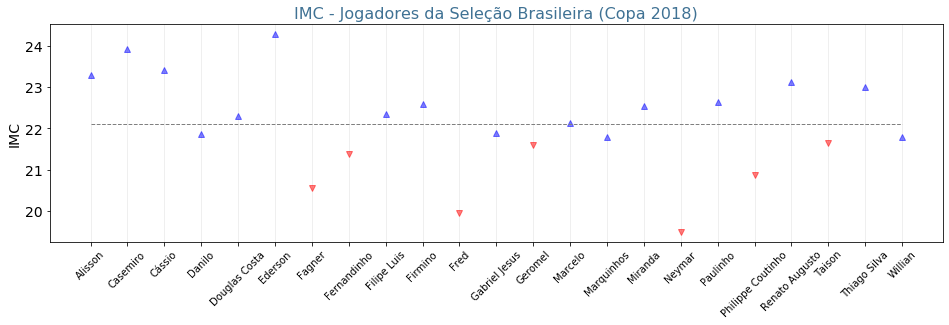
_images/imc.png

Fig. 2 IMC dos jogadores da seleção brasileira da Copa de 2018. [Fonte: ESPN]

Carregue as informações do arquivo e reproduza o gráfico da figura anterior ou crie um similar estilizando-o do seu modo que contenha:

  • a linha tracejada intermediária;

  • marcadores coloridos de modo distinto;

  • eixo com os nomes dos jogadores;

  • linhas de grade;

Obs.: Use a função do numpy load('...'), com a opção allow_pickle=True.

Problema 2: A Taxa Metabólica Basal (TMB) é a quantidade mínima de energia que o ser humano, em repouso, precisa para sobreviver. A Equação de Mifflin - St. Jeor para calcular a TMB em kcal/dia (quilocalorias por dia) de pessoas do sexo masculino é dada por:

\[TMB = 10M + 6.25A - 5I + 5,\]

onde \(M\) é a massa do indivíduo, \(A\) sua altura e \(I\) sua idade.

[Fonte: Wiikipedia]

Usando a equação de Mifflin - St. Jeor:

  • calcule a energia necessária total para a manutenção vital de todos os jogadores da seleção de 2018 durante um ano inteiro, isto é, a TMB anual. Considere 1 ano = 365 dias.

  • calcule a TMB anual do time inteiro para o quinquenio 2020 - 2024. Assuma o início do período em 1 de janeiro de 2020 e que nenhuma alteração na escalação do time ocorrerá no período.

  • plote um gráfico em que o eixo x deve corresponder ao quinquênio e o eixo y ao total da TMB para todos os jogadores em cada ano. Use marcadores do tipo 'o'.

  • qual é o valor total em kcal no final de 2024?

Obs: Note que a idade dos jogadores se altera com o tempo. Isto é, após o quinquênio estarão 5 anos mais velhos e a TMB para cada um será diferente a cada ano.

Problema 3: O movimento executado por uma bola de futebol ao ser chutada a partir do campo por um jogador é similar ao movimento parabólico de um projétil. A velocidade da bola \(V_b\) pode ser calculada pela expressão:

\[V_b = V_p\left( \dfrac{M_p}{M_p + M_b} \right)(1 + e),\]

onde \(V_p\) é a velocidade da perna do chutador, \(M_p\) é a massa da perna do chutador, \(M_b\) é a massa da bola e \(e\) é o coeficiente de restituição da bola.

O alcance \(a\) é a medida horizontal máxima que a bola atinge a partir do ponto de lançamento de acordo com um certo ângulo em que é lançada. Como conhecemos da Física Básica, a fórmula para o alcance é dada por:

\[a = \dfrac{V_b^2\textrm{sen}(2\alpha)}{g}\]

Diante disso, considere os seguintes dados:

  • A massa da bola de futebol profissional é de 400 gramas e seu coeficiente de restituição é 0.7.

  • A massa da perna de um jogador equivale a 10% de sua massa.

  • A velocidade da perna de um jogador é de 20 m/s.

  • A constante gravitacional equivale a 9.8 m/s2.

Assuma que um campo de futebol profissional “padrão FIFA” possui área de 100 x 68 2. Além disso, defina um Whole-Field Kicker (WFK) o jogador que, chutando uma bola a um ângulo de 45 graus, consegue transportá-la de gol a gol, ou seja de uma linha de fundo a outra, e como Not Whole-Field Kicker (not WFK) aquele que não consegue realizar esta proeza.

Usando os dados disponíveis na tabela dos jogadores da seleção de 2018:

  • determine os jogadores que são “WFK” e os “not WFK”, bem como a quantidade de jogadores em cada classe.

  • determine quem é o WFK do time que chuta mais longe.

  • determine qual é o menor alcance entre os chutes.

  • plote um gráfico do tipo jogador x alcance, colorindo os “not WFK” com marcadores com borda vermelha e cor de face branca.

[Fonte: Physics of Kicking a Soccer Ball]

Problema 4: Em 1835, o astrônomo James Inman desenvolveu a fórmula de Haversine. A fórmula de haversine (ou de haverseno) é uma equação usada em navegação para fornecer distâncias entre dois pontos de uma esfera a partir de suas latitudes e longitudes. É um caso especial de uma fórmula mais geral de trigonometria esférica, a lei dos haversines, que relaciona os lados e ângulos de um triângulo contido em uma superfície esférica.

A distância mais curta \(d\) entre dois pontos sobre uma esfera de raio \(R\) cujas latitudes são \((\phi_1,\phi_2)\) e longitudes \((\theta_1,\theta_2)\) é dada por:

\[d = 2R \, \textrm{arcsen}\big(\sqrt{ \textrm{hav}(\phi_2 - \phi_1) + \cos(\phi_1)\cos(\phi_2)\textrm{hav}(\theta_2 - \theta_1) } \big),\]

onde \(\textrm{hav}(\alpha) = \textrm{sen}^2\big(\frac{\alpha}{2}\big)\) é a função haverseno de um ângulo \(\alpha\).

A tabela abaixo lista os 5 aeroportos mais movimentados do mundo em 2014, com latitudes e longitudes dadas em graus.

IATA

Aeroporto

\(\phi\)

\(\theta\)

FRA

Frankfurt

50.026

8.543

DEN

Denver International

39.862

-104.673

BKK

Suvarnabhumi

13.681

100.747

SYD

Sydney Kingsford-Smith

-33.946

151.177

GRU

Guarulhos

-23.432

-46.47

Tarefas:

  • Escreva uma função para calcular a distância mais curta em quilômetros entre dois pontos quaisquer sobre a superfície da Terra (considere \(R = 6378.1\) km) dadas as suas latitudes e longitudes.

  • Use esta função para calcular as distâncias dois-a-dois para todos os aeroportos da tabela acima dadas não só as latitudes e longitudes, mas também os seus códigos IATA.

  • Construa uma matriz numérica \(M\) de correlação de distâncias estritamente triangular inferior com base na ordem alfabética do código IATA. Note que uma matriz estritamente triangular inferior é possui zeros em todas as posições \(M_{ij}\), exceto quando \(i > j\). Logo, não é necessário computar duas vezes um mesmo trajeto, por exemplo, a distância de FRA a DEN será a mesma de DEN a FRA. (Vide exemplo de uma matriz de distâncias aqui)

  • Determine \(i\) e \(j\) tais que \(M_{ij}\) é máxima, bem como o valor de \(M_{ij}\).

Laboratório 3 Laboratório 5