Projeto Final¶
Métodos Computacionais
Nota: use 3 dígitos de precisão para arredondar as respostas (round(x,3)).
Motivação¶
A Fig. 4 mostra perfis laterais do automóvel Tesla Model 3 em sua forma original e aproximada.

Fig. 4 Perfis do modelo Tesla 3: original e aproximado.¶
Considere que o perfil aproximado da carcaça do Tesla Model 3 corresponde ao plano de corte médio (\(x\)-\(z\)) perpendicular ao vetor diretor que determina o eixo normal ao papel \(y\) (largura do veículo). A Fig. 5 mostra esboços do perfil aproximado, em destaque, bem como uma visão tridimensional que o replica ao longo da terceira dimensão (largura).
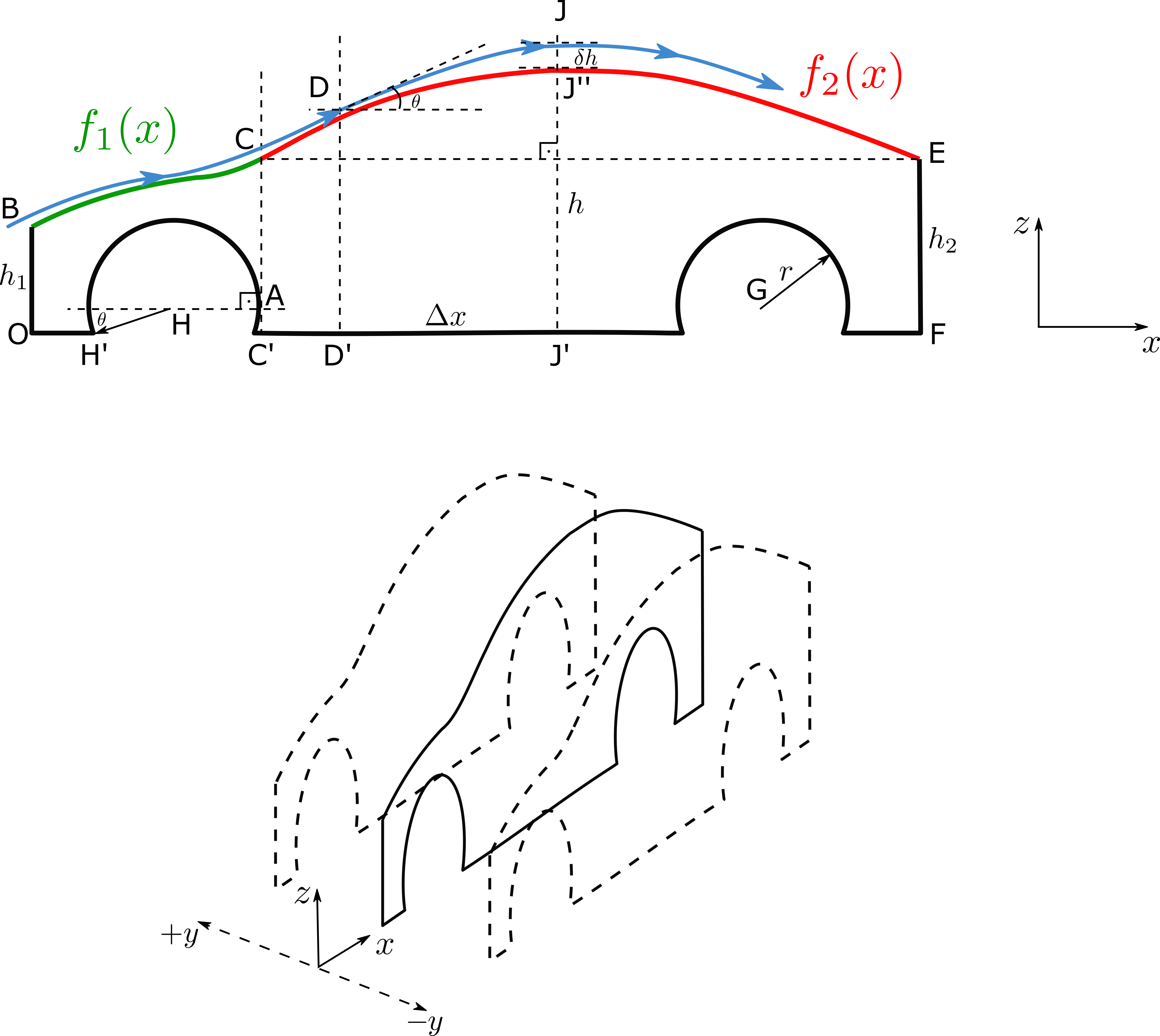
Fig. 5 Perfil cotado do modelo Tesla 3: perfis 2D e 3D.¶
Dados de entrada¶
Considere os seguintes dados do problema, onde \(m(\overline{AB})\), por exemplo, representa a medida do segmento \(\overline{AB}\).
\(m(\overline{OF}) = 4.694 \, m\) (comprimento do veículo)
\(m(\overline{HG}) = 2.875 \, m\) (wheelbase)
\(m(\overline{OC'}) = 0.26 \, m(OF)\)
\(m(\overline{J'J''}) = h = 1.443 \, m\)
\(m(\overline{HH'}) = r = 0.254 \, m\)
\(m(\overline{EF}) = 0.196m(\overline{OF}) \, m\)
\(m(\overline{AC'}) = 0.028m(\overline{OF}) \, m\)
\(\Delta x = 0.36m(\overline{HG})\)
\(2y = 1.849 \, m\) (largura)
Adicionalmente, considere que:
O ponto \(O\) é a origem do plano \((x,z)\) e ponto médio do segmento de comprimento \(2y\) (largura).
O ponto \(B\) possui a mesma coordenada \(z\) do ponto que, juntamente com \(H\), produz um segmento paralelo ao segmento \(\overline{OB}\).
O ponto \(C'\) é a projeção de \(C\).
O ponto \(A\) é tangente ao arco da roda dianteira.
Perfil da carcaça¶
Consideramos duas funções polinomiais, \(z = f_1(x)\) e \(z = f_2(x)\), para aproximar o perfil total \(z = f(x)\) da carcaça do veículo, dividido entre a parte do capô (cor verde) e o teto (cor vermelha). O perfil é definido por:
onde
e
Problema 1 (Volume de carcaça)¶
Determine o volume \(V\) da carcaça do Tesla 3 assumindo o perfil aproximado supracitado e que a área da figura do plano médio replica-se de maneira constante por translação deste plano ao longo do eixo \(y\) (para a direção positiva \(+y\) e negativa \(-y\)), assim perfazendo uma largura medindo \(w\) (Veja Fig. 5). Note que a área no plano médio em questão está limitada acima pela função \(f(x)\) e abaixo, pela função \(g(x) = 0\) (eixo \(x\)).
Use o seguinte roteiro para a solução:
Calcular o valor do ângulo \(\theta\).
Calcular a área do setor circular representativo do espaço ocupado pelas rodas (note que a geometria do setor circular no perfil médio estende-se ao longo da terceira dimensão tanto para a roda dianteira quanto traseira).
Calcule o valor de \(h_1\).
Calcule a área líquida OBCC’, ou seja, excluindo-se a área do setor circular dianteiro.
Calcule a área líquida C’CEF, ou seja, excluindo-se a área do setor circular traseiro.
Calcule o volume usando a hipótese de translação.
Nota: observe que, para os itens 4 e 5, é necessário calcular integrais. Veja a seção Calculando integrais numericamente.
Problema 2 (Movimento de gotícula)¶
Considere que o Tesla 3 está em movimento em uma Autobanh alemã e que, em um certo momento da viagem, uma massa de água respingue sobre o capô. Na Fig. 5, representamos a trajetória executada por uma gotícula de água dessa massa que resvala o capô do automóvel e descola-se do para-brisa exatamente no ponto \(D\), cujas coordenadas são dadas por \((x_D,y_D) = (1.2 + 0.082m(\overline{OF}),h_2 + 0.055m(\overline{OF}))\), a uma velocidade inicial \(V = 1.5 \, m/s\).
Suponha que a gotícula realize um movimento perfeitamente parabólico atingindo a altura máxima no ponto \(J\), que dista verticalmente de \(\delta h\) do teto do automóvel, e horizontalmente de \(\Delta x\) do ponto de descolamento. Determine:
o valor de \(\delta h\), em metros;
o valor de \(\Delta x\), em metros;
a coordenada \(x\), em metros, do veículo em que a gotícula atinge a altura máxima;
o tempo, em segundos, que a gotícula leva para realizar o movimento parabólico completo em segundos.
Nota: use as equações usuais para o movimento de um projétil tomando \((x_D,y_D)\) como ponto de lançamento e assuma a constante de gravidade igual a \(9.81 \, m/s^2\).
Problema 3 (Análise de veículos elétricos)¶
A planilha smart-vehicle-epa-2020.xlsx agrega informações sobre modelos de automóveis movidos a eletricidade e/ou gasolina vendidos nos Estados Unidos e a pontuação deles no âmbito da economia verde (emissão de gases de efeito estufa, poluição do ar etc.)
Usando a biblioteca Pandas:
Leia a planilha em um DataFrame.
Identifique todos os modelos que são movidos a gasolina/eletricidade.
Exporte um arquivo chamado
gas-elet.csvcontendo apenas 4 colunas com as seguintes informações acerca dos modelos encontrados no item 2:
Model
Fuel
Air Pollution Score
Greenhouse Gas Score
APÊNDICE: Calculando integrais numericamente¶
Nesta seção, mostramos como calcular integrais definidas a uma variável numericamente.
Considere a integral \(\int_a^b f(x) \, dx\), onde \(f(x)\) é assumida contínua no intervalo \([a,b]\).
Em Python, podemos calcular o valor desta integral apenas aproximadamente. Para isso, precisamos definir a função a ser integrada como uma função usual do Python, determinar o intervalo de integração e importar a função quad do submódulo scipy.integrate. As funções matemáticas podem ser carregadas a partir do Numpy.
# importação
import numpy as np
from scipy.integrate import quad
Exemplo: Calcule o valor de \(\int_0^2 x^2 + 4 \, dx\)
a,b = 0,2
def f(x):
return x**2 + 4
I,e = quad(f,a,b)
print(f'O valor da integral é I = {round(I,3)} u.a. com erro e = {e}')
O valor da integral é I = 10.667 u.a. com erro e = 1.1842378929335001e-13
A Fig. 6 representa esta integral.
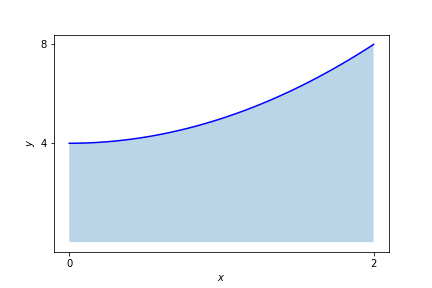
Fig. 6 Área sob o gráfico da função \(\int_0^2 x^2 + 4 \, dx\)¶
Exemplo: Calcule o valor de \(\int_{-\pi/2}^{2\pi} \frac{3}{4}\cos(x)e^x - \frac{x^{1/3}}{2x}\)
a,b = -np.pi/2, 2*np.pi
def f(x):
return 3/4*np.cos(x)*np.exp(x-5) - x**1/3/2*x
I,e = quad(f,a,b)
print(f'O valor da integral é I = {round(I,3)} u.a. com erro e = {e}')
O valor da integral é I = -12.642 u.a. com erro e = 2.013685733235114e-12
A Fig. 7 representa esta integral.
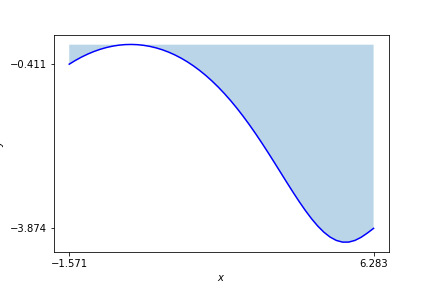
Fig. 7 Área sob o gráfico da função \(\int_{-\pi/2}^{2\pi} \frac{3}{4}\cos(x)e^x - \frac{x^{1/3}}{2x}\)¶