.ipynb .pdf

Contents

Tópicos complementares sobre o numpy

Nesta aula, faremos uma explanação sobre os seguintes tópicos complementares:

• Funções universais (ufuncs)

• Currying

• Agregações

• Ordenação

• Entrada e saída de arquivos

Funções universais

Funções universais (universal functions, ou ufuncs) é o nome dado a qualquer função que pode operar sobre todos os elementos de um array nos moldes da computação vetorizada. Já aprendemos várias ufuncs do numpy como sqrt, cos, exp e random.rand.

Temos diversos tipos de ufuncs, porém, vamos dar exemplos de ufuncs unárias e binárias.

• ufunc unária: é aquela que usa um único array como argumento. Por exemplo, quando fazemos algo como y = np.sqrt(x), x é o único array usado de modo que \(\sqrt{x}\) para cada elemento de x seja o resultado em y.

• ufunc binária: é aquela que usa dois arrays para produzir um resultado.

Ufuncs também podem produzir mais de um array como resultado, mas você aprenderá mais sobre isto durante a graduação. Aqui vamos mostrar apenas um exemplo: modf, uma função unária que é capaz de separar as partes inteira e fracionária de um array contendo números de ponto flutuante (float).

Exemplos de ufuncs unárias

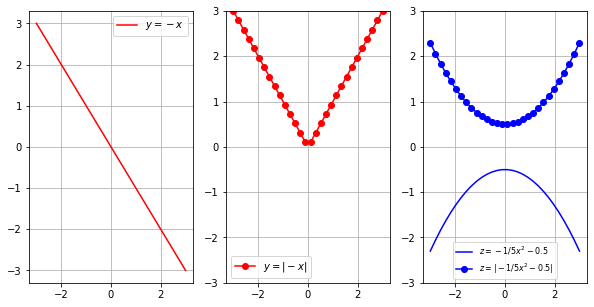
abs, fabs

Calcula a função valor absoluto (módulo)

import numpy as np
import matplotlib.pyplot as plt # auxiliar 

x = np.linspace(-3,3,30) # domínio

# y = f(x) = -x 
y = -x; 
ya = np.abs(y) # <===

# 
z = -1/5*x**2 - 0.5 # 
za = np.fabs(z) # <====

plt.figure(figsize=(10,5))

plt.subplot(131)
plt.plot(x,y,'r',label='$y=-x$'); plt.grid(); plt.legend()

plt.subplot(132)
plt.plot(x,ya,'o-r',label='$y=|-x|$'); plt.ylim(-3,3); plt.grid(); plt.legend()

plt.subplot(133)
plt.plot(x,z,'b',x,za,'-bo');\
         plt.ylim(-3,3); plt.grid();\
         plt.legend(['$z=-1/5x^2 - 0.5$','$z=| -1/5x^2 - 0.5 |$'],fontsize=8,loc='lower center');

floor, round e ceil

• floor aproxima números usando a função “piso” (maior inteiro menor ou igual ao número).

• round aproxima números usando a função “arredondamento” (inteiro mais próximo do número).

• ceil aproxima números usando a função “teto” (menor inteiro maior ou igual ao número).

x = np.sort(np.random.rand(10)*8) # <====

f = np.floor(x)
r = np.round(x)
c = np.ceil(x) 

plt.plot(x,r,'og',alpha=0.3,ms=12,label='round(x)');
plt.plot(x,f,'vb',label='floor(x)');
plt.plot(x,c,'^r',label='ceil(x)');

print('x | floor(x) | round(x) | ceil(x)')
for i in range(len(x)):    
    print('{0:.2f} | {1:.1f} | {2:.1f} | {3:.1f}'.format(x[i],f[i],r[i],c[i]))
plt.legend();

x | floor(x) | round(x) | ceil(x)
0.33 | 0.0 | 0.0 | 1.0
1.48 | 1.0 | 1.0 | 2.0
2.83 | 2.0 | 3.0 | 3.0
3.82 | 3.0 | 4.0 | 4.0
3.99 | 3.0 | 4.0 | 4.0
4.31 | 4.0 | 4.0 | 5.0
5.34 | 5.0 | 5.0 | 6.0
5.67 | 5.0 | 6.0 | 6.0
6.35 | 6.0 | 6.0 | 7.0
6.78 | 6.0 | 7.0 | 7.0

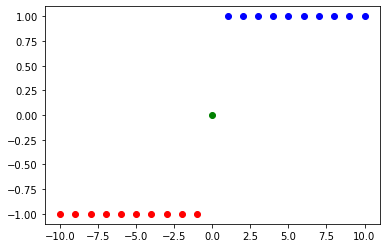
sign

Retorna o “sinal” do número:

• -1, se negativo

• 0, se zero

• 1, se positivo

Isto é:

\[\begin{split} f(x) = \begin{cases} -1,& \text{se }x < 0 \\ 0,& \text{se }x = 0 \\ 1,& \text{se }x > 0 \end{cases} \end{split}\]

x = np.linspace(-10,10,21)
s = np.sign(x)
plt.plot( x[ x < 0 ], s[ x < 0 ],'ro');
plt.plot( x[ x == 0 ], s[ x == 0 ],'go');
plt.plot( x[ x > 0 ], s[ x > 0],'bo');

modf

Separa parte inteira e fracionária de um número.

x = np.sort(np.random.rand(8)*10) # <=====

f, i = np.modf(x) # desempacota as partes fracionária e inteira em f, i 

print('x | i | f')
for v in range(len(x)):    
    print('{0:.8f} | {1:.0f} | {2:.8f}'.format(x[v],i[v],f[v]))

x | i | f
4.51015228 | 4 | 0.51015228
4.72162018 | 4 | 0.72162018
4.98194012 | 4 | 0.98194012
7.70060614 | 7 | 0.70060614
7.81969068 | 7 | 0.81969068
8.31883238 | 8 | 0.31883238
9.36442290 | 9 | 0.36442290
9.45267047 | 9 | 0.45267047

Exemplos de ufuncs binárias

multiply

Multiplica os elementos do primeiro array pelos elementos do segundo array.

x = np.linspace(-10,10,21) # numeros
y = np.linspace(0,20,21) # numeros

xy = np.multiply(x,y)

for i in range(len(x)):
    print('{0:.0f}*{1:.0f} = {2:.0f}'.format(x[i], y[i], xy[i]))

-10*0 = -0
-9*1 = -9
-8*2 = -16
-7*3 = -21
-6*4 = -24
-5*5 = -25
-4*6 = -24
-3*7 = -21
-2*8 = -16
-1*9 = -9
0*10 = 0
1*11 = 11
2*12 = 24
3*13 = 39
4*14 = 56
5*15 = 75
6*16 = 96
7*17 = 119
8*18 = 144
9*19 = 171
10*20 = 200

power

Eleva os elementos no primeiro array à potência especificada pelos elementos do segundo array.

x = np.linspace(-10,10,21) # numeros
exps = np.linspace(0,20,21) # expoentes
xe = np.power(x,exps)
for i in range(len(x)):
    print('{0:.0f}**{1:.0f} = {2:.0f}'.format(x[i], exps[i], xe[i]))

-10**0 = 1
-9**1 = -9
-8**2 = 64
-7**3 = -343
-6**4 = 1296
-5**5 = -3125
-4**6 = 4096
-3**7 = -2187
-2**8 = 256
-1**9 = -1
0**10 = 0
1**11 = 1
2**12 = 4096
3**13 = 1594323
4**14 = 268435456
5**15 = 30517578125
6**16 = 2821109907456
7**17 = 232630513987207
8**18 = 18014398509481984
9**19 = 1350851717672992000
10**20 = 100000000000000000000

Currying

Currying é o processo de derivar novas funções a partir de funções existentes pela aplicação parcial de argumentos.

Por exemplo:

• Defina uma UDF;

def pot_a(x,y,a):
    return np.power(x,y) + a # eleva x a y e soma a 

• Use a UDF em uma segunda função de modo que um de seus argumentos seja fornecido por esta segunda função;

x = np.array([1,2,3])
y = np.array([3,4,5])

segunda_funcao = lambda k: pot_a(x,y,k) # currying em a 
segunda_funcao(3)

array([  4,  19, 246])

Acima, dizemos que o argumento a de pot_a sofreu currying porque foi substituído pelo valor k, fornecido pela lambda segunda_funcao.

Agregações

Agregações (ou reduções) são funções de bastante utilidade em matemática e estatística para calcular somas, médias e outras grandezas ao longo do eixo de um array. Daremos dois exemplos: sum (soma) e mean (média).

sum

Suponha que tenhamos uma matriz como a seguinte:

A = np.random.randint(0,100,(3,3))
A

array([[ 0, 91, 61],
       [66,  2,  3],
       [92, 24, 18]])

• Para calcular a soma de todos os seus elementos, podemos usar a função np.sum ou o método .sum:

np.sum(A) # como função 

357

A.sum() # como método

357

• Para calcular a soma dos elementos ao longo das colunas (somar cada linha), podemos fazer:

np.sum(A, axis = 1) # soma por linhas

array([152,  71, 134])

Ou seja, isto é equivalente a:

np.array( [ sum(A[0,:]), sum(A[1,:]), sum(A[2,:]) ] )

array([152,  71, 134])

• Para calcular a soma dos elementos ao longo das linhas (somar cada coluna), podemos fazer:

np.sum(A,axis = 0) # soma por colunas

array([158, 117,  82])

Ou seja, isto é equivalente a:

np.array( [ sum(A[:,0]), sum(A[:,1]), sum(A[:,2]) ] )

array([158, 117,  82])

mean

O cálculo da média aritmética pode ser realizado da mesma forma.

np.mean(A), A.mean(), np.mean(A) == A.mean()

(39.666666666666664, 39.666666666666664, True)

np.mean(A,axis=1) # média por linhas

array([50.66666667, 23.66666667, 44.66666667])

 np.mean(A,axis=0) # média por colunas

array([52.66666667, 39.        , 27.33333333])

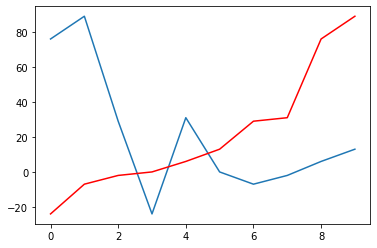
Ordenação

Na plotagem das funções “piso”, “teto” e “arredondamento”, usamos ordenação. Para ordenar elementos de um array, use sort.

desordenado = np.random.randint(-30,100,10)
ordenado = np.sort(desordenado)
ordenado

array([-24,  -7,  -2,   0,   6,  13,  29,  31,  76,  89])

plt.plot(desordenado);
plt.plot(ordenado,'r');

Entrada e saída de arquivos

Podemos ler o conteúdo de um arquivo através do Numpy, bem como escrever e salvar um arquivo novo quando o propósito é trabalhar com matrizes de dados. Mostraremos duas maneira de trabalhar com arquivos:

• manipulando arquivos de dados simples com extensão .txt.

• manipulando arquivos especiais do numpy com extensão .npy.

Os arquivos .npy são do tipo binário e puros do numpy. Eles possuem propriedades de eficiência e servem para armazenarem informações pertinentes ao numpy. Ou seja, o numpy tem seu próprio tipo de arquivo.

Exemplo: O arquivo data/consumo.txt (disponibilizado junto com o material) contém uma matriz de dados contendo a massa em quilogramas (2a. coluna) e o consumo medido em quilômetros por litro (3a. coluna) de alguns modelos de automóveis. Você pode usar um editor de texto para visualizar o arquivo. Ele deve se parecer com

modelo	massa (kg)	C (km/litro)
Focus	1198	11.90
Crown Victoria	1715	6.80
Expedition	2530	5.53
Explorer	2014	6.38
F-150	2136	5.53
Fusion	1492	8.50
Taurus	1652	7.65
Fit	1168	13.60
Accord	1492	9.78
CR-V	1602	8.93
Civic	1192	11.90
Ridgeline	2045	6.38

Podemos ler o conteúdo deste arquivo e salvá-lo diretamente em uma matriz com a função loadtxt('caminho_do_arquivo').

M = np.loadtxt('data/consumo.txt')
M

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-22-864339eea655> in <module>
----> 1 M = np.loadtxt('data/consumo.txt')
      2 M

~/anaconda3/lib/python3.7/site-packages/numpy/lib/npyio.py in loadtxt(fname, dtype, comments, delimiter, converters, skiprows, usecols, unpack, ndmin, encoding, max_rows)
   1137         # converting the data
   1138         X = None
-> 1139         for x in read_data(_loadtxt_chunksize):
   1140             if X is None:
   1141                 X = np.array(x, dtype)

~/anaconda3/lib/python3.7/site-packages/numpy/lib/npyio.py in read_data(chunk_size)
   1065 
   1066             # Convert each value according to its column and store
-> 1067             items = [conv(val) for (conv, val) in zip(converters, vals)]
   1068 
   1069             # Then pack it according to the dtype's nesting

~/anaconda3/lib/python3.7/site-packages/numpy/lib/npyio.py in <listcomp>(.0)
   1065 
   1066             # Convert each value according to its column and store
-> 1067             items = [conv(val) for (conv, val) in zip(converters, vals)]
   1068 
   1069             # Then pack it according to the dtype's nesting

~/anaconda3/lib/python3.7/site-packages/numpy/lib/npyio.py in floatconv(x)
    761         if '0x' in x:
    762             return float.fromhex(x)
--> 763         return float(x)
    764 
    765     typ = dtype.type

ValueError: could not convert string to float: 'Focus'

Por que o erro?

Porque a primeira coluna contém strings. Para ignorá-las, selecionamos as colunas que queremos usar com usecols.

M = np.loadtxt('data/consumo.txt',usecols=(1,2)) # usa 2a. e 3a. colunas 
M

array([[1198.  ,   11.9 ],
       [2530.  ,    5.53],
       [2014.  ,    6.38],
       [2136.  ,    5.53],
       [1492.  ,    8.5 ],
       [1652.  ,    7.65],
       [1168.  ,   13.6 ],
       [1492.  ,    9.78],
       [1602.  ,    8.93],
       [1192.  ,   11.9 ],
       [2045.  ,    6.38]])

Podemos operar livremente com este array. Digamos que queiramos calcular o consumo para uma viagem de 250 km com cada veículo. Fazemos simplesmente:

c200 = M[:,1]*250
c200

array([2975. , 1382.5, 1595. , 1382.5, 2125. , 1912.5, 3400. , 2445. ,
       2232.5, 2975. , 1595. ])

Agora, digamos que queiramos salvar um novo arquivo com esta coluna adicional. Primeiro, concatenamos este resultado na matriz.

M2 = np.concatenate((M,c200[:,np.newaxis]),axis=1) # concatena
M2

array([[1198.  ,   11.9 , 2975.  ],
       [2530.  ,    5.53, 1382.5 ],
       [2014.  ,    6.38, 1595.  ],
       [2136.  ,    5.53, 1382.5 ],
       [1492.  ,    8.5 , 2125.  ],
       [1652.  ,    7.65, 1912.5 ],
       [1168.  ,   13.6 , 3400.  ],
       [1492.  ,    9.78, 2445.  ],
       [1602.  ,    8.93, 2232.5 ],
       [1192.  ,   11.9 , 2975.  ],
       [2045.  ,    6.38, 1595.  ]])

Enfim, podemos usar a função savetxt('caminho_do_arquivo',array) para exportar o conteúdo de array para um arquivo. No caso a seguir, nosso novo arquivo tem o nome de 05a-consumo-tabela.txt.

np.savetxt('data/consumo-tabela.txt',M2) # salva o conteúdo de M2 em arquivo

Para verificar que ambos os arquivos estão salvos, faça:

%%script bash 
ls data/*.txt # lista os arquivos .txt nesta pasta.

data/consumo-tabela.txt
data/consumo.txt

%%script

O comando %%script permite que uma instrução em outra linguagem de programação (shell script) seja executada. No caso anterior, a instrução diz: “no diretório em que estou, liste para mim todos os arquivos com extensão .txt”.

%who e %whos

O comando mágico %who (significando Who is here?, “Quem está aqui?”) serve para listarmos todas as variáveis presentes no atual espaço de trabalho. Já %whos expande as informações acerca delas.

%who

A	 M	 M2	 c	 c200	 desordenado	 exps	 f	 i	 
np	 ordenado	 plt	 pot_a	 r	 s	 segunda_funcao	 v	 x	 
xe	 xy	 y	 ya	 z	 za	 

%whos

Variable         Type        Data/Info
--------------------------------------
A                ndarray     3x3: 9 elems, type `int64`, 72 bytes
M                ndarray     11x2: 22 elems, type `float64`, 176 bytes
M2               ndarray     11x3: 33 elems, type `float64`, 264 bytes
c                ndarray     10: 10 elems, type `float64`, 80 bytes
c200             ndarray     11: 11 elems, type `float64`, 88 bytes
desordenado      ndarray     10: 10 elems, type `int64`, 80 bytes
exps             ndarray     21: 21 elems, type `float64`, 168 bytes
f                ndarray     8: 8 elems, type `float64`, 64 bytes
i                int         20
np               module      <module 'numpy' from '/Us<...>kages/numpy/__init__.py'>
ordenado         ndarray     10: 10 elems, type `int64`, 80 bytes
plt              module      <module 'matplotlib.pyplo<...>es/matplotlib/pyplot.py'>
pot_a            function    <function pot_a at 0x7fe7dad528c0>
r                ndarray     10: 10 elems, type `float64`, 80 bytes
s                ndarray     21: 21 elems, type `float64`, 168 bytes
segunda_funcao   function    <function <lambda> at 0x7fe7dad52050>
v                int         7
x                ndarray     3: 3 elems, type `int64`, 24 bytes
xe               ndarray     21: 21 elems, type `float64`, 168 bytes
xy               ndarray     21: 21 elems, type `float64`, 168 bytes
y                ndarray     3: 3 elems, type `int64`, 24 bytes
ya               ndarray     30: 30 elems, type `float64`, 240 bytes
z                ndarray     30: 30 elems, type `float64`, 240 bytes
za               ndarray     30: 30 elems, type `float64`, 240 bytes

Plotagem básica com matplotlib Manipulação de dados com pandas