.ipynb .pdf

Contents

Introdução à Computação Simbólica com sympy

Motivação

Neste ponto do curso, você já aprendeu a realizar operações matemáticas elementares com Python. Por exemplo, se lhe for dado o valor do raio \(R\), você consegue facilmente computar a área \(\pi R^2\) de um círculo. Todavia, o valor de \(\pi\) que você obtém é finito. As instruções abaixo verificam isto.

from math import pi
print(pi)
3.141592653589793

Pense, no entanto, se você pudesse realizar o cálculo desta área de maneira “exata”. Matematicamente falando, é impossível fazer isto pois \(\pi\) é um número irracional – o imbróglio desta constante é longo na história da Matemática. Porém, a computação simbólica permite que operemos com \(\pi\) como se fosse simplesmente um símbolo com precisão infinita. Embora 15 casas decimais, como o valor exemplificado acima, sejam suficientes para a maioria dos cálculos do mundo real, a computação simbólica permite que trabalhemos com modelos abstratos que servem a uma diversidade de propósitos.

Aliás, quando se diz que 3.141592653589793 é um valor razoavelmente aceitável, isto é verdade até mesmo para cálculos em escala astronômica. A equipe de engenharia da NASA explica que, usando este valor para calcular o perímetro de uma circunferência com diâmetro igual a 25 bilhões de milhas, o erro de cálculo é próximo de 1,5 polegada [NASA]. Até aí, nada mal para uma aproximação!

O que é Computação Simbólica e para que serve?

Computação Simbólica (CS) é uma subárea de estudo da matemática e da ciência da computação que se preocupa em resolver problemas usando objetos simbólicos representáveis em um computador. Esses problemas surgem em muitas aplicações em ciências naturais, pesquisa básica, na indústria e principalmente no desenvolvimento de softwares para computação avançada denominados sistemas de computação algébrica (SCAs).

A CS existente em um SCA é aplicada em álgebra computacional, projetos assistidos por computação (CAD), raciocínio automatizado, gestão do conhecimento, lógica computacional e sistemas formais de verificação. O desenvolvimento da CS depende da integração de basicamente três campos: softwares matemáticos, álgebra computacional e lógica computacional [RISC/JKU]. Em casos mais avançados, a CS é útil para solucionar equações da macroeconomia, manipular números para a finalidade de criptografia e criar modelos probabilísticos [Kotzé], [Cohen].

Principais SCAs

Alguns SCAs são populares de longa data, tais como Maple, Mathematica e MuPad. Entretanto, são comerciais e costumam ter licenças custosas, embora ofereçam versões com desconto para estudantes. Algumas alternativas robustas de uso livre são Scilab, Sagemath, Octave e o próprio módulo sympy. Uma lista completa de SCAs está disponível na [Wikipedia].

Por que sympy?

O objetivo principal do sympy é ser uma biblioteca de manipulação simbólica para Python. Ele começou a ser desenvolvido em 2006 e atualmente está na versão 1.5.1, lançada em dezembro de 2019 na página oficial [sympy.org]. As principais características do módulo são as seguintes:

• é gratuito;

• é baseado inteiramente em Python;

• é leve e independente.

Objetos numéricos x objetos simbólicos

Importaremos os módulos math e sympy para ver algumas diferenças entre objetos numéricos e simbólicos.

import math as mt
import sympy as sy
sy.init_printing(pretty_print=True) # melhor impressão de símbolos

mt.pi # numérico

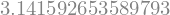
sy.pi # simbólico

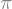
Verifiquemos com type.

type(mt.pi)

float

type(sy.pi) # é um objeto simbólico

sympy.core.numbers.Pi

Vejamos mais um exemplo:

mt.sqrt(2)

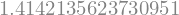
sy.sqrt(2)

type(mt.sqrt(2))

float

type(sy.sqrt(2)) # é um objeto simbólico

sympy.core.power.Pow

Função x método

Na aula anterior destacamos que print e type são “funções” similares àquelas do tipo \(y = f(x)\) em Matemática. Em Python, essas “funções” recebem o nome de função mesmo.

Porém, há módulos que possuem métodos, que para seu entendimento, podem ser vistos como “funções” também. Porém, função e método são conceitos levemenete distintos.

Para aplicarmos funções usamos parênteses envolvendo um ou mais parâmetros.

No caso acima, mt.sqrt(2) mostra que sqrt age como uma função e o número 2 é seu único parâmetro. Note, além disso, que o sympy também possui a sua própria função sqrt, que é de uma natureza distinta. Ela é um objeto sympy.core.power.Pow. Não precisamos entender isso agora, mas basta saber que ela pertence a um submódulo do sympy.

Por outro lado, também aprendemos que o conjugado de um número complexo z (tipo complex) pode ser obtido como z.conjugate(). Esta forma “sem parâmetros” indica que conjugate é um método do objeto z.

A partir deste ponto, poderemos ver situações como as seguintes:

• f(x): a função f é aplicada ao parâmetro x

• a.f(): f é um método sem parâmetro do objeto a

• a.f(x): f é um método com parâmetro x do objeto a

A partir do último exemplo, podemos dizer que um método é, na verdade, uma função que pertence a um objeto.

Atribuições com símbolos

Podemos atribuir símbolos a variáveis usando a função symbols.

x = sy.symbols('x')
y = sy.symbols('y')

x e y são símbolos sem valor definido.

x

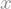
y

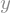
Podemos operar aritmeticamente com símbolos e obter uma expressão simbólica como resultado.

z = sy.symbols('z')
x*y + z**2/3 + sy.sqrt(x*y - z)

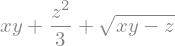
Exemplo: escreva o produto notável \((x - y)^2\) como uma expressão simbólica.

x**2 - 2*x*y + y**2

Note que o nome da variável não tem a ver com o nome do símbolo. Poderíamos fazer o seguinte:

y = sy.symbols('x') # y é variável; x é símbolo
y

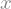
Atribuição por desempacotamento

Também poderíamos realizar as atribuições anteriores da seguinte forma:

x, y, z = sy.symbols('x y z')

Alfabeto de símbolos

O sympy dispõe de um submódulo chamado abc do qual podemos importar símbolos para letras latinas (maiúsculas e minúsculas) e gregas (minúsculas).

from sympy.abc import a,b,c,alpha,beta,gamma
(a + 2*b - 3*c)*(alpha/3 + beta/2 - gamma) # símbolico

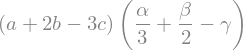
from sympy.abc import D,G,psi,theta
D**a * G**b * psi**c * theta**2 # símbolico

Nota: algumas letras já são usadas como símbolos especiais, tais como O, que indica “ordem” e I, que é o complexo \(i\). Neste caso, cuidado deve ser tomado com nomes de variáveis

sy.I # imaginário simbólico

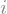
type(sy.I)

sympy.core.numbers.ImaginaryUnit

Símbolos com nomes genéricos

Para criar símbolos genéricos, temos de usar symbols ou Symbol.

sem_nocao = sy.symbols('nada')
sem_nocao

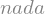
muito_louco = sy.Symbol('massa')
muito_louco

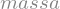
Variáveis e símbolos

sem_medo = sem_nocao + 2
sem_medo 

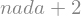
soma = muito_louco + 2
muito_louco = 3 # 'muito_louco' aqui não é o simbólico
soma

Substituição

A operação de substituição permite que:

1. substituamos variáveis por valores numéricos para avaliar uma expressão ou calcular valores de uma função em um dado ponto.

2. substituamos uma subexpressão por outra.

Para tanto, procedemos da seguinte forma:

expressao.subs(variavel,valor)

Exemplo: considere o polinômio \(P(x) = 2x^3 - 4x -6\). Calcule o valor de \(P(-1)\), \(P(e/3)\), \(P(\sqrt{3.2})\).

from sympy.abc import x 
P = 2*x**3 - 4*x - 6
P1 = P.subs(x,-1)
Pe3 = P.subs(x,mt.e/3)
P32 = P.subs(x,mt.sqrt(3.2))
print(P1, Pe3, P32)

-4 -8.13655822141297 -1.70674948320040

Exemplo: sejam \(f(x) = 4^x\) e \(g(x) = 2x - 1\). Compute o valor da função composta \(f(g(x))\) em \(x = 3\).

f = 4**x
fg = f.subs(x,2*x - 1)

fg.subs(x,3)

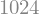
Poderíamos também fazer isso com um estilo “Pythônico”:

fg = 4**x.subs(x,2*x - 1).subs(x,3)
fg

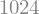
Exemplo: se \(a(x) = 2^x\), \(b(x) = 6^x\) e \(c(x) = \cos(x)\), compute o valor de \(a(x)b(c(x))\) em \(x = 4\)

a = 2**x
b = 6**x
c = sy.cos(x)
(a * b.subs(x,c)).subs(x,4)

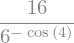
Ou, de modo direto:

valor = ( 2**x * ( 6**x.subs(x,sy.cos(x))) ).subs(x,4)
valor

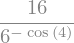
Avaliação de expressão em ponto flutuante

Note que a expressão anterior não foi computada em valor numérico. Para obter seu valor numérico, podemos usar o método evalf.

valor.evalf()

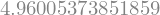
Precisão arbitrária

evalf permite que escolhamos a precisão do cálculo impondo o número de dígitos de precisão. Por exemplo, a última expressão com 20 dígitos de precisão seria:

valor.evalf(20)

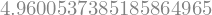
Com 55, seria:

valor.evalf(55)

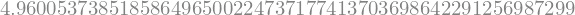
E com 90 seria:

valor.evalf(90)

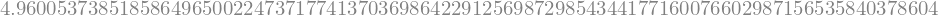
Exemplo: calcule o valor de \(e\) com 200 dígitos de precisão.

sy.exp(1).evalf(200)

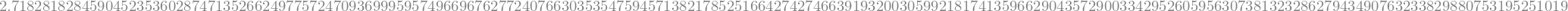
Funções predefinidas x funções regulares

Vamos apresentar aqui três grupos de funções que podem ser criadas em Python para nos auxiliar ao longo do curso sem, no entanto, nos aprofundaremos nos detalhes de cada um.

Como dissemos em um momento anterior, a linguagem Python possui um core que contém um conjunto de funções já prontas que podemos usar, como é o caso de print(), type() e até mesmo int() e float() para operações de casting. Essas funções podem ser chamadas de predefinidas (built-in functions). Ou seja, são aquelas funções “já existentes”. Exemplos adicionais seriam as funções do módulo math.

Suponhamos, porém, que você vasculhe módulos e mais módulos atrás de uma função que faça exatamente o que você quer, mas não a encontra. O que você faz? Você a cria! Podemos fazer isto de uma maneira usando uma “palavra-chave” (keyword) chamada def da seguinte forma:

def f(x):
    (...)
    return y

A instrução acima permite que você crie uma função chamada f da qual x é um argumento e y é um valor de retorno, indicado por uma segunda “palavra-chave”, return. Funções definidas por você dessa maneira são chamadas de regulares, normais – pelo fato de serem programadas de um modo regular, seguindo a “normalidade” da linguagem –, ou ainda definidas pelo usuário (do inglês user-defined functions, ou simplesmente UDF). Por conveniência, vamos nos referir a elas por este acrônimo elegante: UDF.

Uma UDF permite que você abstraia seu pensamento para criar basicamente o que quiser dentro dos limites da linguagem Python. Cabe, apesar disso, fazermos as seguintes ressalvas:

• uma UDF pode ter zero ou mais argumentos, tantos quantos se queira;

• uma UDF pode ou não ter valor de retorno;

Vamos entender as UDFs com exemplos.

Exemplo: Suponha que você é um(a) analista de dados do mercado imobiliário e está estudando o impacto do repasse de comissões pagas a corretores mediante vendas de imóveis. Você, então, começa a raciocinar e cria um modelo matemático bastante simples que, antes de tudo, precisa calcular o valor do repasse a partir do preço de venda.

Se \(c\) for o percentual de comissão, \(V\) o valor da venda do imóvel e \(r\) o valor a ser repassado para o corretor, então, a função a ser definida é

\[r(V) = c\, V,\]

assumindo que \(c\) seja um valor fixo.

Digamos que \(c\) corresponda a 1.03% do valor da venda do imóvel. Neste caso podemos criar uma UDF para calcular \(r\) para nós da seguinte forma:

def repasse(V): 
    r = 0.0103*V  
    return r

Para \(V = \, R\$ \, 332.130,00\):

repasse(332130)

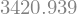
O que é necessário observar:

• def vem seguido pelo nome da função (repasse) após um espaço;

• o nome precede os argumentos, enclausurados por parênteses (V). Neste caso, temos apenas um argumento, que é V;

• após o nome, os dois-pontos (:) são obrigatórios e significam mais ou menos “o que esta função faz será definido da seguinte maneira”

• a instrução r = 0.0103*V é o escopo da função, que deve ser escrito em uma ou mais linhas indentadas (pressione TAB para isso, ou use 4 espaços)

• o valor de retorno, se houver, é posto na última linha do escopo.

Podemos atribuir os valores do argumento e resultado a variáveis:

V = 332130
rep = repasse(V)
rep

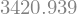
Nomes iguais de variável e função são permissíveis.

repasse = repasse(V) # 'repasse' à esquerda é uma variável; à direita, função
print(repasse)

3420.939

Todavia, isto pode ser confuso e é bom evitar.

O estilo “Pythônico” de escrever permite que o valor de retorno não seja explicitamente declarado. No escopo

...
    r = 0.0103*V  
    return r

a variável r não é necessária.

Python é inteligente para permitir o seguinte:

def repasse(V): 
    return 0.0103*V

# note que aqui não indentamos a linha. 
# Logo esta instrução NÃO pertence ao escopo da função.
repasse(V)

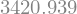
Podemos criar uma função para diferentes valores de c e V usando dois argumentos:

def repasse_c(c,V): # esta função tem outro nome
    return c*V

c = 0.0234 # equivaleria a uma taxa de repasse de 2.34%
V = 197432 # o valor do imóvel agora é R$ 197.432,00
repasse_c(c,V)

A ordem dos argumentos importa:

V = 0.0234 # este deveria ser o valor de c
c = 197432 # este deveria ser o valor de V
repasse_c(c,V)

Por que o valor resultante é o mesmo? Porque a operação no escopo da função é uma multiplicação, c*V, que é comutativa independentemente do valor das variáveis. Porém, digamos que um segundo modelo tenha uma forma de cálculo distinta para a comissão dada por

\[r_2(V) = c^{3/5} \, V\]

Neste caso:

def repasse_2(c,V):
    return c**(3/5)*V

V = 197432
c = 0.0234

repasse_2(c,V)

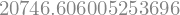
Porém, se trocarmos o valor das variáveis, a função repasse_2 calculará um valor distinto. Embora exista um produto também comutativo, o expoente 3/4 modifica apenas o valor de c.

# variáveis com valores trocados
c = 197432
V = 0.0234

repasse_2(c,V)

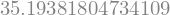
A ordem com que escrevemos os argumentos tem importância relativa aos valores que passamos e ao que definimos:

# variáveis com valores corretos
V = 197432
c = 0.0234

def repasse_2_trocada(V,c): # V vem antes de c
    return c**(3/5)*V
    
repasse_2_trocada(V,c)

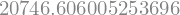
Mas,

# os valores das variáveis estão corretos, 
# mas foram passados para a função na ordem errada
repasse_2_trocada(c,V) 

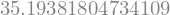
e

# a ordem dos argumentos está de acordo com a que foi definida
# mas os valores das variáveis foram trocados
V = 197432
c = 0.0234
repasse_2_trocada(c,V) 

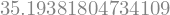
Modelos matemáticos simbólicos

A partir do que aprendemos, podemos definir modelos matemáticos completamente simbólicos.

from sympy.abc import c,V

def repasse_2_simbolica(c,V):
    return c**(3/5)*V

Se chamarmos esta função, ela será um objeto simbólico.

repasse_2_simbolica(c,V)

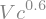
Atribuindo em variável:

rep_simb = repasse_2_simbolica(c,V)

type(rep_simb) # é um objeto simbólico

sympy.core.mul.Mul

Exemplo: Suponha, agora, que seu modelo matemático de repasse deva considerar não apenas um percentual \(c\) pré-estabelecido, mas também um valor de “bônus” adicional concedido como prêmio pela venda do imóvel. Considere, então, que o valor deste bônus seja \(b\). Diante disso, nosso novo modelo teria uma fórmula como a seguinte:

\[r_3(V) = c\,V + b\]

Simbolicamente:

# importaremos apenas o símbolo b, 
# uma vez que c e V já foram importados 
# como símbolos anteriormente
from sympy.abc import b 

def r3(V):
    return c*V + b

rep_3 = r3(V)
rep_3

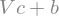
Substituindo valores

Podemos usar a função subs para atribuir quaisquer valores para o modelo.

Exemplo: \(c = 0.119\)

rep_3.subs(c,0.119) # substituindo para c

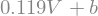
Exemplo: \(c = 0.222\)

rep_3.subs(c,0.222) # substituindo para c

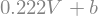
Exemplo: \(c = 0.222\) e \(b = 12.0\)

rep_3.subs(c,0.222).subs(b,12.0) # substituindo para c, depois para b

Substituição múltipla

O modo anterior de substituição não é “Pythônico”. Para substituirmos mais de uma variável de uma vez, devemos usar pares ordenados separados por vírgula sequenciados entre colchetes como uma lista. Mais tarde, aprenderemos sobre pares ordenados e listas.

Exemplo: Modifique o modelo \(r_3\) para que \(c = 0.043\) e \(b = 54.0\)

# espaços foram adicionados para dar legibilidade
rep_3.subs( [ (c,0.043), (b,54.0) ] )

Pares ordenados

Em matemática, o conceito de par ordenado pode ser definido pelo conjunto:

\[ X \times Y = \{ (x,y) ; x \in X \text{ e } y \in Y \},\]

onde \(X\) e \(Y\) são conjuntos quaisquer e \(x\) e \(y\) são as coordenadas. Por exemplo, se \(X = Y = \mathbb{R}\), o conjunto acima contém elementos do tipo \((3,2)\), \((-1,3)\), \((\pi,2.18)\) etc. Na verdade, eles formam o conjunto \(\mathbb{R} \times \mathbb{R} = \mathbb{R}^2\), que é exatamente o plano cartesiano.

Logo, a substituição múltipla com subs ocorre da seguinte forma;

• a primeira coordenada é o símbolo;

• a segunda coordenada é o valor que você quer dar para o símbolo.

Exemplo: Calcule \(r_3(V)\) considerando \(c = 0.021\), \(b = 34.0\) e \(V = 432.000\).

# armazenaremos o valor na variável 'valor'
valor = r3(V)

# subsituição 
valor.subs( [ (c,0.021), (b,54.0) ] )

Com o estilo “Pythônico”:

valor = r3(V).subs( [ (c,0.021), (b,54.0) ] ) # 
valor

Podemos seguir esta regra de pares para substituir todos os valores de um modelo simbólico genérico não necessariamente definido através de uma função. Veja o exemplo aplicado a seguir.

Exemplo de aplicação: o índice de caminhabilidade

Estudos empíricos nos EUA mostraram que a caminhabilidade de uma vizinhança impacta substancialmente os preços das casas. A caminhabilidade está relacionada à distância da moradia a locais de amenidades, tais como restaurantes, bares, bibliotecas, mercearias etc.

O índice de caminhabilidade \(W\) para uma vizinhança de casas é uma medida matemática que assume valores no intervalo \([0,1]\). A fórmula é definida por:

\[W(d) = e^{-5 \left( \dfrac{d}{M} \right)^5},\]

onde \(d\) é a distância medida entre a vizinhança (0 metro) e um dado ponto de referência, e \(M\) é a distância máxima de avaliação considerada a partir da qual a caminhabilidade é assumida como nula. Ou seja,

• quando estamos na vizinhança, \(d = 0\), \(W = 1\) e a caminhabilidade é considerada ótima.

• à medida que nos afastamos da vizinhança em direção ao local da amenidade, \(d\) aumenta e o valor \(W\) decai vertiginosamente até atingir o valor limite \(M\) a partir do qual \(W = 0\) e a caminhabilidade é considerada “péssima”.

O índice de caminhabilidade é, portanto, calculado com relação a um ponto de destino definido e a distância deve levar em consideração as vias de circulação (ruas, rodovias etc) e não a distância mais curta (raio do perímetro). Por exemplo, se a distância máxima a ser considerada para a caminhabilidade for \(M = 500 \, m\) , um bar localizado a 100 metros da vizinhança teria um índice de caminhabilidade maior do que o de uma farmácia localizada a 300 m e muito maior do que o de um shopping localizado a 800 m, ainda que muito famoso. Aliás, neste caso, o valor de \(W\) para o shopping seria zero, já que 800 m está além do limite \(M\) estabelecido.

Fonte: De Nadai, M. and Lepri, B. [The economic value of neighborhoods: Predicting real estate prices from the urban environment].

Modelo simbólico

Podemos modelar \(W\) simbolicamente e calcular seu valor para diferentes valores de \(d\) e \(M\) usando a substituição múltipla.

from sympy.abc import d,M,W 

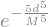
W = sy.exp(-5*(d/M)**5) # função exponencial simbólica
W

Exemplo: A nossa corretora de imóveis gostaria de entender a relação de preços de imóveis para o Condomínio Pedras de Marfim. Considerando \(M = 1 km\), calcule:

• o índice de caminhabilidade \(W_1\) em relação à farmácia Dose Certa, localizada a 222 m do condomínio.

• o índice de caminhabilidade \(W_2\) em relação ao restaurante Sabor da Arte, localizada a 628 m do condomínio.

• o índice de caminhabilidade \(W_3\) em relação ao Centro Esportivo Physicalidade, localizada a 998 m do condomínio.

• o índice de caminhabilidade \(W_4\) em relação à Padaria Dolce Panini, localizada a 1,5 km do condomínio.

# note que 1 km = 1000 m
W1 = W.subs([ (d,222), (M,1000) ]) 
W2 = W.subs([ (d,628), (M,1000) ]) 
W3 = W.subs([ (d,998), (M,1000) ]) 
W4 = W.subs([ (d,1500), (M,1000) ])

Perceba, entretanto, que os valores calculados ainda não são numéricos, como esperado.

W1

W2

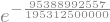
W3

W4

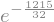
Lembre-se que podemos usar evalf para calcular esses valores. Faremos isso considerando 3 casas decimais.

# reatribuindo todos os valores
W1n = W1.evalf(3)
W2n = W2.evalf(3)
W3n = W3.evalf(3)
W4n = W4.evalf(3)

print('W1 =', W1n, '; ' \
      'W2 =', W2n, '; ' \
      'W3 =', W3n, '; ' \
      'W4 =', W4n)       

W1 = 0.997 ; W2 = 0.614 ; W3 = 0.00708 ; W4 = 3.24e-17

Como era de se esperar, os valores decaem de 0.997 a 3.24e-17, que é um valor considerado nulo em termos de aproximação numérica.

Quebrando instruções com \

A contra-barra \ pode ser usada para quebrar instruções e continuá-las nas próximas linhas, porém não poderá haver nenhum caracter após ela, nem mesmo espaços. Caso contrário, um erro será lançado.

print('Continuando' \
      'na linha abaixo')

Continuandona linha abaixo

# neste exemplo, há um caracter de espaço após \
print('Continuando' \ 
      'na linha abaixo')

  File "<ipython-input-68-322bd86bfa93>", line 2
    print('Continuando' \
                          ^
SyntaxError: unexpected character after line continuation character

O tipo bool

Em Python, temos mais um tipo de dado bastante útil, o bool, que é uma redução de “booleano”. Objetos bool, que têm sua raiz na chamada Álgebra de Boole, são baseados nos conceitos true (verdadeiro) e false, ou 0 e 1 e são estudados em algumas disciplinas, tais como Circuitos Lógicos, Matemática Discreta, Lógica Aplicada, entre outras.

Aprenderemos sobre operadores lógicos mais à frente. Por enquanto, cabe mencionar as entidades fundamentais True e False.

True

True

False

False

type(True)

bool

type(False)

bool

Podemos realizar testes lógicos para concluir verdades ou falsidades quando temos dúvidas sobre objetos e relações entre eles. Por exemplo, retomemos os seguintes valores:

W1

W2

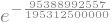
A princípio, é difícil determinar qual dos dois é o maior. Porém, podemos realizar “perguntas” lógicas para o interpretador Python com operadores lógicos. Mostraremos apenas dois exemplos com > e <.

W1 > W2 # isto quer dizer: "W1 é maior do que W2?"

O valor True confirma que o valor de W1 é maior do que W2.

W4 < 0

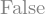
Note que, de acordo com nosso modelo de caminhabilidade, este valor deveria ser zero. Porém, numericamente, ele é uma aproximação para zero. Embora muito pequeno, não é exatamente zero! Por que isso ocorre? Porque o computador lida com uma matemática inexata e aproximada, mas com precisão satisfatória.

Operadores lógicos

Vimos que True e False são os dois valores atribuíves a um objeto de tipo bool. Eles são úteis para testar condições, realizar verificações e comparar quantidades. Vamos estudar operadores de comparação, operadores de pertencimento e operadores de identidade.

Operadores de comparação

A tabela abaixo resume os operadores de comparação utilizados em Python.

operador	significado	símbolo matemático
<	menor do que	\(<\)
<=	menor ou igual a	\(\leq\)
>	maior do que	\(>\)
>=	maior ou igual a	\(\geq\)
==	igual a	\(=\)
!=	diferente de	\(\neq\)

Podemos usá-los para comparar objetos.

Nota: == está relacionado à igualdade, ao passo que = é uma atribuição. São conceitos operadores com finalidade distinta.

2 < 3 # o resultado é um 'bool'

True

5 < 2 # isto é falso

False

2 <= 2 # isto é verdadeiro

True

4 >= 3 # isto é verdadeiro

True

6 != -2 

True

4 == 4 # isto não é uma atribuição! 

True

Podemos realizar comparações aninhadas:

x = 2
1 < x < 3

True

3 > x > 4

False

2 == x > 3 

False

As comparações aninhadas acima são resolvidas da esquerda para a direita e em partes. Isso nos leva a introduzir os seguintes operadores.

operador	símbolo matemático	significado	uso relacionado a
or	\(\vee\)	“ou” booleano	união, disjunção
and	\(\wedge\)	“e” booleano	interseção, conjunção
not	\(\neg\)	“não” booleano	exclusão, negação

# parênteses não são necessários aqui
(2 == x) and (x > 3) # 1a. comparação: 'True'; 2a.: 'False'. Portanto, ambas: 'False'

False

# parênteses não são necessários aqui
(x < 1) or (x < 2) # nenhuma das duas é True. Portanto, 

False

not (x == 2) # nega o "valor-verdade" que é 'True'

False

not x + 1 > 3 # estude a precedência deste exemplo. Por que é 'True'?

True

not (x + 1 > 3) # estude a precedência deste exemplo. Por que também é 'True'?

True

Operadores de pertencimento

A tabela abaixo resume os operadores de pertencimento.

operador	significado	símbolo matemático
in	pertence a	\(\in\)
not in	não pertence a	\(\notin\)

Eles terão mais utilidade quando falarmos sobre sequências, listas. Neste momento, vejamos exemplos com objetos str.

'2' in '2 4 6 8 10' # o caracter '2' pertence à string

True

frase_teste = 'maior do que' 
'maior' in frase_teste

True

'menor' in frase_teste # a palavra 'menor' está na frase

False

1 in 2 # 'in' e 'not in' não são aplicáveis aqui

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-94-5c8c51a582d3> in <module>
----> 1 1 in 2 # 'in' e 'not in' não são aplicáveis aqui

TypeError: argument of type 'int' is not iterable

Operadores de identidade

A tabela abaixo resume os operadores de identidade.

operador	significado
is	“aponta para o mesmo objeto”
is not	“não aponta para o mesmo objeto”

Esses operadores são úteis para verificar se duas variáveis se referem ao mesmo objeto. Exemplo:

a is b
a is not b

• is é True se a e b se referem ao mesmo objeto; False, caso contrário.

• is not é False se a e b se referem ao mesmo objeto; True, caso contrário.

a = 2
b = 3
a is b # valores distintos

False

a = 2
b = a
a is b # mesmos valores

True

a = 2
b = 3
a is not b # de fato, valores não são distintos

True

a = 2
b = a
a is not b # de fato, valores são distintos

False

Equações simbólicas

Equações simbólicas podem ser formadas por meio de Eq e não com = ou ==.

# importação
from sympy.abc import a,b
import sympy as sy 
sy.init_printing(pretty_print=True)

sy.Eq(a,b) # equação simbólica

sy.Eq(sy.cos(a), b**3) # os objetos da equação são simbólicos

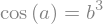
Resolução de equações algébricas simbólicas

Podemos resolver equações algébricas da seguinte forma:

solveset(equação,variável,domínio)

Exemplo: resolva \(x^2 = 1\) no conjunto \(\mathbb{R}\).

from sympy.abc import x
sy.solveset( sy.Eq( x**2, 1), x,domain=sy.Reals)

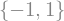
Podemos reescrever a equação como: \(x^2 - 1 = 0\).

sy.solveset( sy.Eq( x**2 - 1, 0), x,domain=sy.Reals)

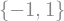
Com solveset, não precisamos de Eq. Logo, a equação é passada diretamente.

sy.solveset( x**2 - 1, x,domain=sy.Reals)

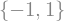
Exemplo: resolva \(x^2 + 1 = 0\) no conjunto \(\mathbb{R}\).

sy.solveset( x**2 + 1, x,domain=sy.Reals) # não possui solução real

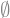
Exemplo: resolva \(x^2 + 1 = 0\) no conjunto \(\mathbb{C}\).

sy.solveset( x**2 + 1, x,domain=sy.Complexes) # possui soluções complexas

Exemplo: resolva \(\textrm{sen}(2x) = 3 + x\) no conjunto \(\mathbb{R}\).

sy.solveset( sy.sin(2*x) - x - 3,x,sy.Reals) # a palavra 'domain' também pode ser omitida.

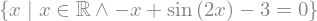
O conjunto acima indica que nenhuma solução foi encontrada.

Exemplo: resolva \(\textrm{sen}(2x) = 1\) no conjunto \(\mathbb{R}\).

sy.solveset( sy.sin(2*x) - 1,x,sy.Reals)

Expansão, simplificação e fatoração de polinômios

Vejamos exemplos de polinômios em uma variável.

a0, a1, a2, a3 = sy.symbols('a0 a1 a2 a3') # coeficientes
P3x = a0 + a1*x + a2*x**2 + a3*x**3 # polinômio de 3o. grau em x
P3x

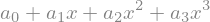
b0, b1, b2, b3 = sy.symbols('b0 b1 b2 b3') # coeficientes
Q3x = b0 + b1*x + b2*x**2 + b3*x**3 # polinômio de 3o. grau em x
Q3x

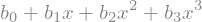
R3x = P3x*Q3x # produto polinomial
R3x

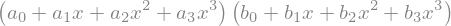
R3x_e = sy.expand(R3x) # expande o produto
R3x_e

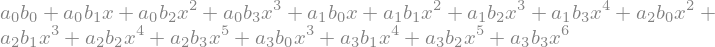
sy.simplify(R3x_e) # simplify às vezes não funciona como esperado

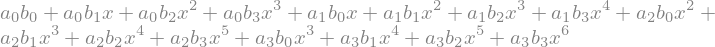
sy.factor(R3x_e) # 'factor' pode funcionar melhor

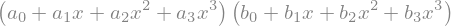
# simplify funciona para casos mais gerais 
ident_trig = sy.sin(x)**2 + sy.cos(x)**2
ident_trig

sy.simplify(ident_trig)

Identidades trigonométricas

Podemos usar expand_trig para expandir funções trigonométricas.

sy.expand_trig( sy.sin(a + b) ) # sin(a+b)

sy.expand_trig( sy.cos(a + b) ) # cos(a+b)

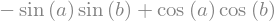
sy.expand_trig( sy.sec(a - b) ) # sec(a-b)

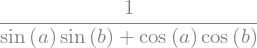
Propriedades de logaritmo

Com expand_log, podemos aplicar propriedades válidas de logaritmo.

sy.expand_log( sy.log(a*b) )

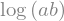
A identidade não foi validada pois a e b são símbolos irrestritos.

a,b = sy.symbols('a b',positive=True) # impomos que a,b > 0

sy.expand_log( sy.log(a*b) ) # identidade validada

sy.expand_log( sy.log(a/b) )

m = sy.symbols('m', real = True) # impomos que m seja um no. real
sy.expand_log( sy.log(a**m) )

Com logcombine, compactamos as propriedades.

sy.logcombine( sy.log(a) + sy.log(b) ) # identidade recombinada

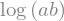
Fatorial

A função factorial(n) pode ser usada para calcular o fatorial de um número.

sy.factorial(m)

sy.factorial(m).subs(m,10) # 10! 

sy.factorial(10) # diretamente

Exemplo: Sejam \(m,n,x\) inteiros positivos. Se \(f(m) = 2m!\), \(g(n) = \frac{(n + 1)!}{n^2!}\) e \(h(x) = f(x)g(x)\), qual é o valor de \(h(2)\)?

from sympy.abc import m,n,x

f = 2*sy.factorial(m)
g = sy.factorial(n + 1)/sy.factorial(n**2)

h = (f.subs(m,x)*g.subs(n,x)).subs(x,4)
h

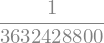
Funções anônimas

A terceira classe de funções que iremos aprender é a de funções anônimas. Uma função anônima em Python consiste em uma função cujo nome não é explicitamente definido e que pode ser criada em apenas uma linha de código para executar uma tarefa específica.

Funções anônimas são baseadas na palavra-chave lambda. Este nome tem inspiração em uma área da ciência da computação chamada de cálculo-\(\lambda\).

Uma função anônima tem a seguinte forma:

lambda lista_de_parâmetros: expressão

Funções anônimas podem são bastante úteis para tornar um código mais conciso.

Por exemplo, na aula anterior, definimos a função

def repasse(V): 
    return 0.0103*V

para calcular o repasse financeiro ao corretor imobiliário.

Com uma função anônima, a mesma função seria escrita como:

repasse = lambda V: 0.0103*V

Não necessariamente temos que atribui-la a uma variável. Neste caso, teríamos:

lambda V: 0.0103*V

<function __main__.<lambda>(V)>

Para usar a função, passamos um valor:

repasse(100000) # repasse sobre R$ 100.000,00

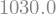
O modelo completo com “bonificação” seria escrito como:

r3 = lambda c,V,b: c*V + b # aqui há 3 parâmetros necessários

Redefinamos objetos simbólicos:

from sympy.abc import b,c,V
r3(b,c,V)

O resultado anterior continua sendo um objeto simbólico, mas obtido de uma maneira mais direta. Podemos usar funções anônimas para tarefas de menor complexidade.

“Lambdificação” simbólica

Usando lambdify, podemos converter uma expressão simbólica do sympy para uma expressão que pode ser numericamente avaliada em outra biblioteca. Essa função desempenha papel similar a uma função lambda (anônima).

expressao = sy.sin(x) + sy.sqrt(x) # expressão simbólica
f = sy.lambdify(x,expressao,"math") # lambdificação para o módulo math
f(0.2) # avalia

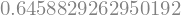
Para avaliações simples como a anterior, podemos usar evalf e subs. A lambdificação será útil quando quisermos avaliar uma função em vários pontos, por exemplo. Na próxima aula, introduziremos sequencias e listas. Para mostrar um exemplo de lambdificação melhor veja o seguinte exemplo.

from numpy import arange # importação de função do módulo numpy

X = arange(40) # gera 40 valores de 0 a 39

X

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
       34, 35, 36, 37, 38, 39])

f = sy.lambdify(x,expressao,"numpy")(X) # avalia 'expressao' em X
f

array([0.        , 1.84147098, 2.32351099, 1.87317082, 1.2431975 ,
       1.2771437 , 2.17007424, 3.30273791, 3.81778537, 3.41211849,
       2.61825655, 2.31663458, 2.9275287 , 4.02571831, 4.73226474,
       4.52327119, 3.71209668, 3.16170813, 3.49165344, 4.50877615,
       5.38508121, 5.41923133, 4.68156445, 3.94961112, 3.99340112,
       4.86764825, 5.86157796, 6.15252835, 5.56240841, 4.72153092,
       4.48919395, 5.16372672, 6.20828093, 6.74447451, 6.36003458,
       5.48789711, 5.00822115, 5.4392244 , 6.46078258, 7.20879338])

Fundamentos de Python para Computação Científica Fundamentos de Matemática Discreta com Python