.ipynb .pdf

Contents

Plotagem básica com matplotlib

Visualização de dados

A visualização de dados é um campo do conhecimento bastante antigo que foi trazido à mostra muito recentemente com a expansão do “Big Data”. Seu principal objetivo é representar dados e informações graficamente por meio de elementos visuais como tabelas, gráficos, mapas e infográficos. Diversas ferramentas estão disponíveis para tornar a interpretação de dados mais clara, compreensível e acessível.

No contexto da análise de dados, a visualização de dados é um componente fundamental para a criação de relatórios de negócios, painéis de instrumentos (dashboards) e gráficos multidimensionais que são aplicáveis às mais diversas disciplinas, tais como Economia, Ciência Política e, principalmente, todo o núcleo de ciências exatas (Matemática, Estatística e Computação).

Em seu livro The Visual Display of Quantitative Information, [Edward Tufte], conhecido como o guru do design aplicado à visualização de dados, afirma que, a cada ano, o mundo produz algo entre 900 bilhões e 2 trilhões de imagens impressas de gráficos. Ele destaca que o design de um gráfico estatístico, por exemplo, é uma matéria universal similar à Matemática e não está atrelado a características únicas de uma linguagem particular. Portanto, aprender visualização de dados para comunicar dados com eficiência é tão importante quanto aprender a Língua Portuguesa para escrever melhor.

Você pode ver uma lista sugestiva de bons blogues e livros sobre visualização de dados nas páginas de aprendizagem do software Tableau [TabelauBlogs], [TabelauBooks].

Data storytelling

Data Storytelling é o processo de “contar histórias através dos dados”. [Cole Knaflic], uma engenheira de dados do Google, ao perceber como a quantidade de informação produzida no mundo às vezes é muito mal lida e comunicada, escreveu dois best-sellers sobre este tema a fim de ajudar pessoas a comunicarem melhor seus dados e produtos quantitativos. Ela argumenta em seu livro Storytelling with Data: A Data Visualization Guide for Business Professionals (Storytelling com Dados: um Guia Sobre Visualização de Dados Para Profissionais de Negócios, na versão em português) que não somos inerentemente bons para “contar uma história” através dos dados. Cole mostra com poucas lições o que devemos aprender para atingir uma comunicação eficiente por meio da visualização de dados.

Plotagem matemática

Plotagem é o termo comumente empregado para o esboço de gráficos de funções matemáticas via computador. Plotar gráficos é uma das tarefas que você mais realizará como futuro(a) cientista ou analista de dados. Nesta aula, nós introduziremos você ao universo da plotagem de gráficos em duas dimensões e ensinar como você pode visualizar dados facilmente com a biblioteca matplotlib. Daremos uma visão geral principalmente sobre a plotagem de funções matemáticas utilizando arrays e recursos de computação vetorizada com numpy já aprendidos. Ao longo do curso, você aprenderá a fazer plotagens mais interessantes de cunho estatístico.

A biblioteca matplotlib

Matplotlib é a biblioteca Python mais conhecida para plotagem 2D (bidimensional) de arrays. Sua filosofia é simples: criar plotagens simples com apenas alguns comandos, ou apenas um. John Hunter [History], falecido em 2012, foi o autor desta biblioteca. Em 2008, ele escreveu que, enquanto buscava uma solução em Python para plotagem 2D, ele gostaria de ter, entre outras coisas:

• gráficos bonitos com pronta qualidade para publicação;

• capacidade de incorporação em interfaces gráficas para desenvolvimento de aplicações;

• um código fácil de entender e de manusear.

O matplotlib é um código dividido em três partes:

1. A interface pylab: um conjunto de funções predefinidas no submódulo matplotlib.pyplot.

2. O frontend: um conjunto de classes responsáveis pela criação de figuras, textos, linhas, gráficos etc. No frontend, todos os elementos gráficos são objetos ainda abstratos.

3. O backend: um conjunto de renderizadores responsáveis por converter os gráficos para dispositivos onde eles podem ser, de fato, visualizados. A [renderização] é o produto final do processamento digital. Por exemplo, o backend PS é responsável pela renderização de [PostScript]. Já o backend SVG constroi gráficos vetoriais escaláveis ([Scalable Vector Graphics].

Veja o conceito de [Canvas].

Sessões interativas do matplotlib

Sessões interativas do matplotlib são habilitadas através de um [comando mágico]:

• Em consoles, use %matplotlib;

• No Jupyter notebook, use %matplotlib inline.

Lembre que na aula anterior usamos o comando mágico %timeit para temporizar operações.

Para usar plenamente o matplotlib nesta aula, vamos usar:

%matplotlib inline
from matplotlib import pyplot as plt

A segunda instrução também pode ser feita como

import matplotlib.pyplot as plt

em que plt é um alias já padronizado.

# chamada padrão
%matplotlib inline
import matplotlib.pyplot as plt

Criação de plots simples

Vamos importar o numpy para usarmos os benefícios da computação vetorizada e plotar nossos primeiros exemplos.

import numpy as np

x = np.linspace(-10,10,50)
y = x
plt.plot(x,y); # reta y = x 

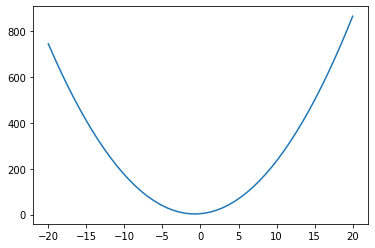
Exemplo: plote o gráfico da parábola \(f(x) = ax^2 + bx + c\) para valores quaisquer de \(a,b,c\) no intervalo \(-20 \leq x \leq 20\).

x = np.linspace(-20,20,50)

a,b,c = 2,3,4
y = a*x**2 + b*x + c # f(x)
plt.plot(x,y);

Podemos definir uma função para plotar a parábola:

def plota_parabola(a,b,c):
    x = np.linspace(-20,21,50)
    y = a*x**2 + b*x + c
    plt.plot(x,y)

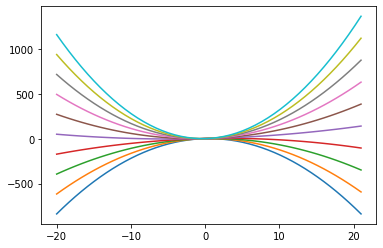
Agora podemos estudar o que cada coeficiente faz:

# mude o valor de a e considere b = 2, c = 1

for a in np.linspace(-2,3,10):
    plota_parabola(a,2,1)

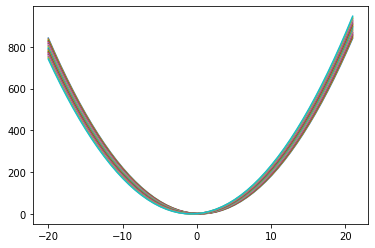
# mude o valor de b e considere a = 2, c = 1

for b in np.linspace(-2,3,20):
    plota_parabola(2,b,1)

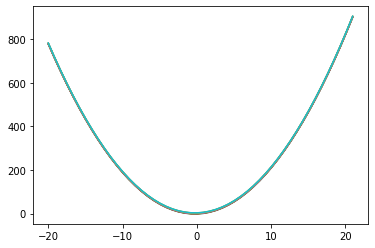
# mude o valor de c e considere a = 2, b = 1

for c in np.linspace(-2,3,10):
    plota_parabola(2,1,c) # por que você não vê muitas mudanças?

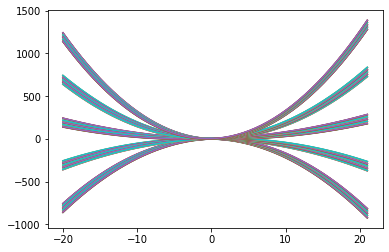
# mude o valor de a, b e c 

valores = np.linspace(-2,3,5)
for a in valores:
    for b in valores:
        for c in valores:
            plota_parabola(a,b,c)

Exemplo: plote o gráfico da função \(g(t) = a\cos(bt + \pi)\) para valores quaisquer de \(a\) e \(b\) no intervalo \(0 \leq t \leq 2\pi\).

t = np.linspace(0,2*np.pi,50,endpoint=True) # t: ângulo

a, b = 1, 1
plt.plot(t,a*np.cos(b*t + np.pi));

b = 2
plt.plot(t,a*np.cos(b*t + np.pi));

b = 3
plt.plot(t,a*np.cos(b*t + np.pi));

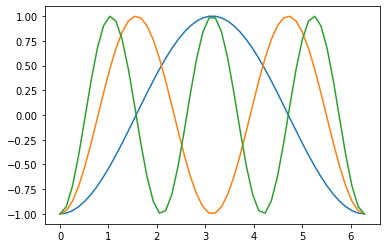
As cores e marcações no gráfico são todas padronizadas. Vejamos como alterar tudo isto.

Alteração de propriedades e estilos de linhas

Altere:

• cores com color ou c,

• espessura de linha com linewidth ou lw

• estilo de linha com linestyle ou ls

• tipo de símbolo marcador com marker

• largura de borda do símbolo marcardor com markeredgewidth ou mew

• cor de borda do símbolo marcardor com markeredgecolor ou mec

• cor de face do símbolo marcardor com markerfacecolor ou mfc

• transparência com alpha no intervalo [0,1]

g = lambda a,b: a*np.cos(b*t + np.pi) # assume t anterior

# estude cada exemplo
# a ordem do 3o. argumento em diante pode mudar
plt.plot(t,g(1,1),color='c',linewidth=5,linestyle='-.',alpha=.3)
plt.plot(t,g(1,2),c='g',ls='-',lw='.7',marker='s',mfc='y',ms=8)
plt.plot(t,g(1,3),c='#e26d5a',ls=':', marker='d',mec='k',mew=2.0);

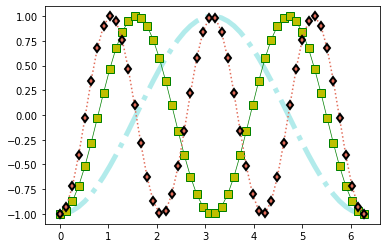
Cores e estilo de linha podem ser especificados de modo reduzido e em ordens distintas usando um especificador de formato.

plt.plot(t,g(1,1),'yv') # amarelo; triângulo para baixo;
plt.plot(t,g(1,2),':c+') # pontilhado; ciano; cruz;
plt.plot(t,-g(2,2),'>-.r'); # triangulo direita; traço-ponto; vermelho;

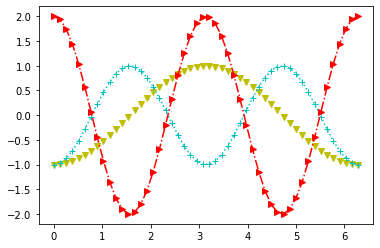
Plotagem múltipla

O exemplo acima poderia ser feito como plotagem múltipla em 3 blocos do tipo (x,y,'fmt'), onde x e y são as informações dos eixos coordenados e fmt é uma string de formatação.

plt.plot(t,g(1,1),'yv', t,g(1,2),':c+', t,-g(2,2),'>-.r'); # 3 blocos sequenciados

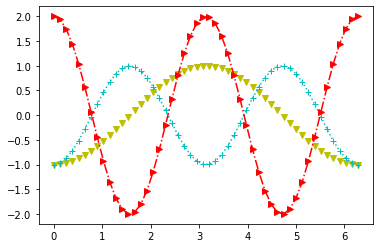
Para verificar todas as opções de propriedades e estilos de linhas, veja plt.plot?.

Especificação de figuras

Use plt.figure para criar um ambiente de figura e altere:

• a largura e altura (em polegadas) com figsize = (largura,altura). O padrão é (6.4,4.8).

• a resolução (em pontos por polegadas) com dpi. O padrão é 100.

• a cor de fundo (background) com facecolor. O padrão é w (branco).

Exemplo: Plote os gráficos de \(h_1(x) = a\sqrt{x}\) e \(h_2(x) = be^{\frac{x}{c}}\) para valores de a,b,c e propriedades acima livres.

x = np.linspace(0,10,50,endpoint=True)

h1, h2 = lambda a: a*np.sqrt(x), lambda b,c: b*np.exp(x/c) 

plt.figure(figsize=(8,6), dpi=200, facecolor='#e0eeee')
plt.plot(x,h1(.9),x,h2(1,9));

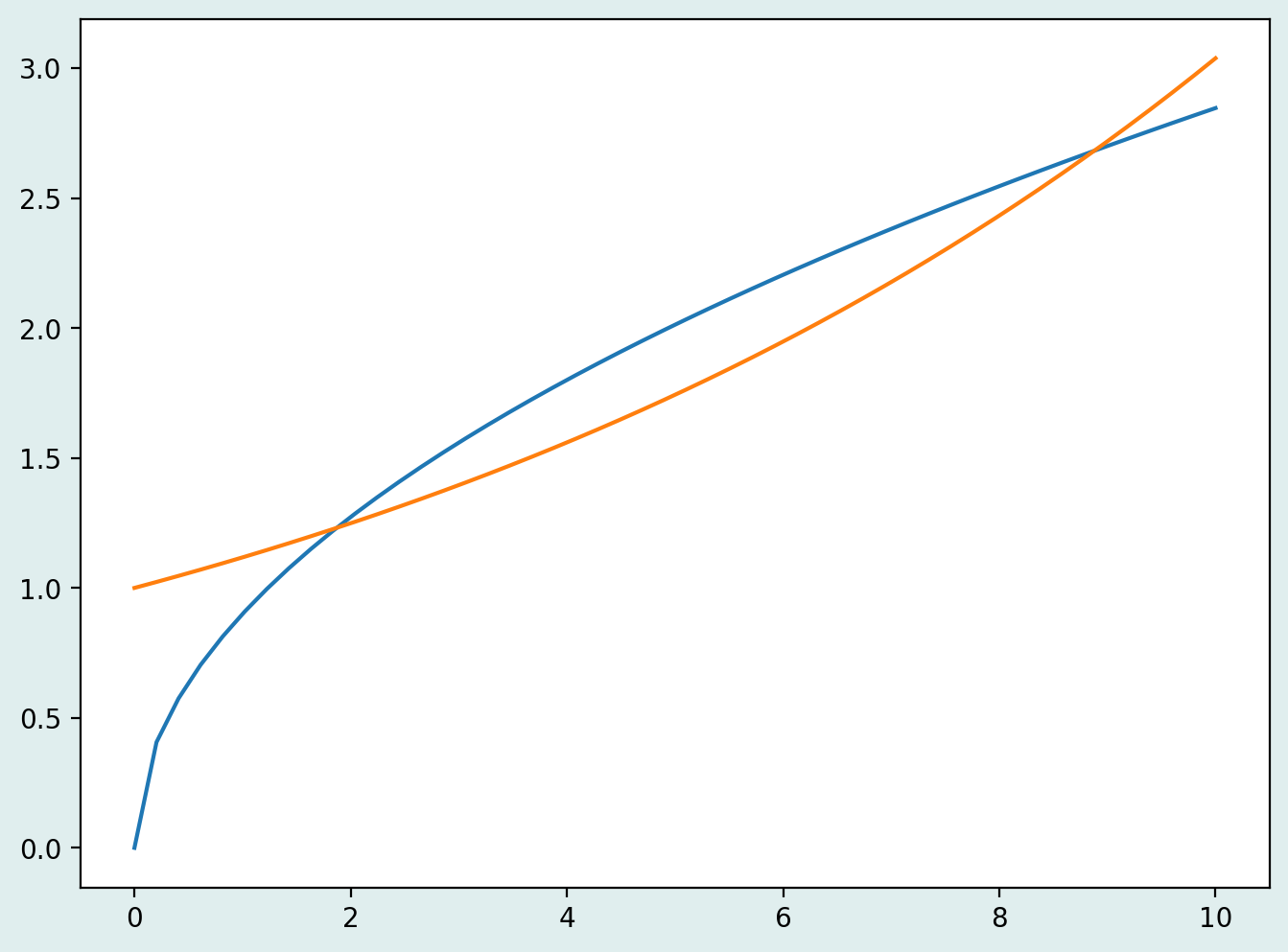
Alterando limites e marcações de eixos

Altere:

• o intervalo do eixo x com xlim

• o intervalo do eixo y com ylim

• as marcações do eixo x com xticks

• as marcações do eixo y com yticks

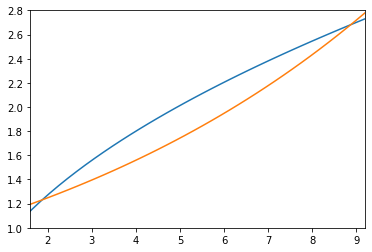
plt.plot(x,h1(.9),x,h2(1,9)); plt.xlim(1.6,9.2); plt.ylim(1.0,2.8);

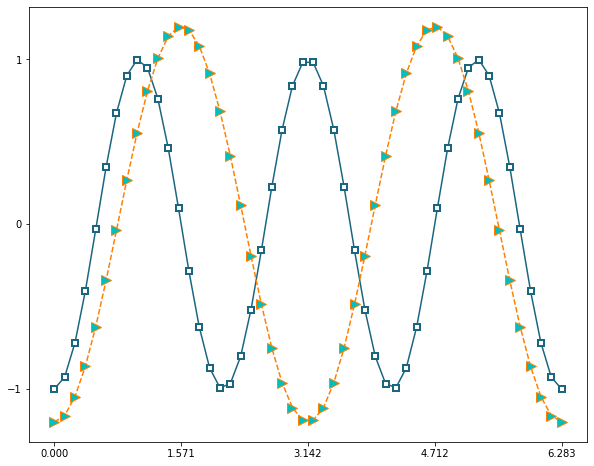
plt.figure(figsize=(10,8))

plt.plot(t,g(1,3),c=[0.1,0.4,0.5],marker='s',mfc='w',mew=2.0);
plt.plot(t,g(1.2,2),c=[1.0,0.5,0.0],ls='--',marker='>',mfc='c',mew=1.0,ms=10);

plt.xticks([0, np.pi/2,np.pi,3*np.pi/2,2*np.pi]); # lista de múltiplos de pi
plt.yticks([-1, 0, 1]); # 3 valores em y

Especificando texto de marcações em eixos

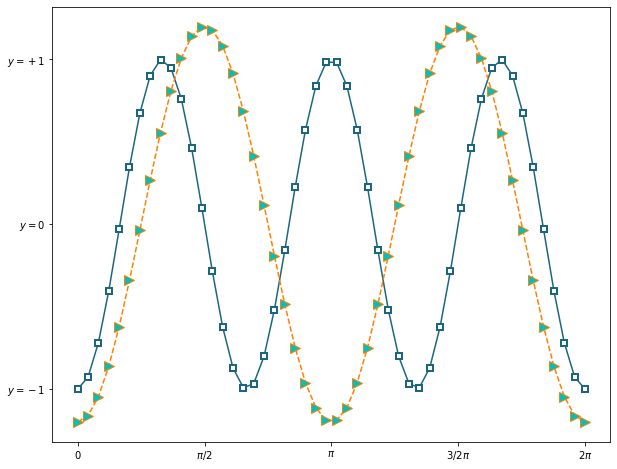
Podemos alterar as marcações das ticks passando um texto indicativo. No caso anterior, seria melhor algo como:

plt.figure(figsize=(10,8))

plt.plot(t,g(1,3),c=[0.1,0.4,0.5],marker='s',mfc='w',mew=2.0);
plt.plot(t,g(1.2,2),c=[1.0,0.5,0.0],ls='--',marker='>',mfc='c',mew=1.0,ms=10);

# o par de $...$ formata os números na linguagem TeX
plt.xticks([0, np.pi/2,np.pi,3*np.pi/2,2*np.pi], ['$0$','$\pi/2$','$\pi$','$3/2\pi$','$2\pi$']); 
plt.yticks([-1, 0, 1], ['$y = -1$', '$y = 0$', '$y = +1$']); 

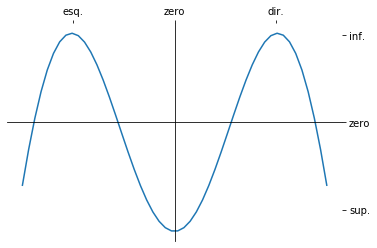
Deslocamento de eixos principais

Os eixos principais podem ser movidos para outras posições arbitrárias e as bordas da área de plotagem desligadas usando spine.

# plotagem da função
x = np.linspace(-3,3)
plt.plot(x,x**1/2*np.sin(x)-0.5); # f(x) = √x*sen(x) - 1/2
ax = plt.gca()  

ax.spines['right'].set_color('none') # remove borda direita
ax.spines['top'].set_color('none') # remove borda superior

ax.spines['bottom'].set_position(('data',0)) # desloca eixo para x = 0
ax.spines['left'].set_position(('data',0)) # desloca eixo para y = 0

ax.xaxis.set_ticks_position('top') # desloca marcações para cima
ax.yaxis.set_ticks_position('right') # desloca marcações para a direita

plt.xticks([-2,0,2]) # altera ticks de x
ax.set_xticklabels(['esq.','zero','dir.']) # altera ticklabels de x

plt.yticks([-0.4,0,0.4]) # altera ticks de y
ax.set_yticklabels(['sup.','zero','inf.']); # altera ticklabels de y

Inserção de legendas

Para criarmos:

• uma legenda para os gráficos, usamos legend.

• uma legenda para o eixo x, usamos xlabel

• uma legenda para o eixo y, usamos ylabel

• um título para o gráfico, usamos title

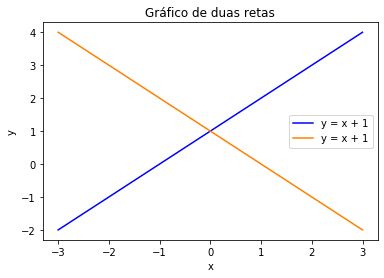
Exemplo: plote o gráfico da reta \(f_1(x) = x + 1\) e da reta \(f_2(x) = 1 - x\) e adicione uma legenda com cores azul e laranja.

plt.plot(x, x + 1,'-b', label = 'y = x + 1' )
plt.plot(x, 1-x, c = [1.0,0.5,0.0], label = 'y = 1 - x'); # laranja: 100% de vermelho, 50% verde
plt.legend(loc = 'best') # 'loc=best' : melhor localização da legenda
plt.xlabel('x'); plt.ylabel('y'); plt.title('Gráfico de duas retas');

Localização de legendas

Use loc=valor para especificar onde posicionar a legenda. Use plt.legend? para verificar as posições disponíveis para valor. Vide tabela de valores Location String e Location Code.

plt.plot(np.nan,np.nan,label='upper right'); # nan : not a number
plt.legend(loc=1); # usando número

plt.plot(np.nan,np.nan,label='loc=1');
plt.legend(loc='upper right'); # usando a string correspondente

Alteração de tamanho de fonte

Para alterar o tamanho da fonte de legendas, use fontsize.

plt.plot(np.nan,np.nan,label='legenda');

FSx, FSy, FSleg, FStit = 10, 20, 30, 40

plt.xlabel('Eixo x',c='b', fontsize=FSx)
plt.ylabel('Eixo y',c='g', fontsize=FSy)
plt.legend(loc='center', fontsize=FSleg); 
plt.title('Título', c='c', fontsize=FStit);

Anotações simples

Podemos incluir anotações em gráficos com a função annotate(texto,xref,yref)

plt.plot(np.nan,np.nan);
plt.annotate('P (0.5,0.5)',(0.5,0.5));
plt.annotate('Q (0.1,0.8)',(0.1,0.8));

Exemplo: gere um conjunto de 10 pontos \((x,y)\) aleatórios em que \(0.2 < x,y < 0.8\) e anote-os no plano.

# gera uma lista de 10 pontos satisfazendo a condição
P = []
while len(P) != 10:
    xy = np.round(np.random.rand(2),1) 
    test = np.all( (xy > 0.2) & (xy < 0.8) )
    if test:
        P.append(tuple(xy))

# plota o plano
plt.figure(figsize=(8,8))
plt.xlim(0,1)
plt.ylim(0,1)

for ponto in P:    
    plt.plot(ponto[0],ponto[1],'o')
    plt.annotate(f'({ponto[0]},{ponto[1]})',ponto,fontsize=14)

Problema: o código acima tem um problema. Verifique que len(P) = 10, mas ele não plota os 10 pontos como gostaríamos de ver. Descubra o que está acontecendo e proponha uma solução.

Multiplotagem e eixos

No matplotlib, podemos trabalhar com a função subplot(m,n,p) para criar múltiplas figuras e eixos independentes como se cada figura fosse um elemento de uma grande “matriz de figuras” de m linhas e n colunas, enquanto p é o índice da figura (este valor será no máximo o produto mxn). A função funciona da seguinte forma.

• Exemplo 1: suponha que você queira criar 3 figuras e dispô-las em uma única linha. Neste caso, m = 1, n = 3 e p variará de 1 a 3, visto que mxn = 3.

• Exemplo 2: suponha que você queira criar 6 figuras e dispô-las em 2 linhas e 3 colunas. Neste caso, m = 2, n = 3 e p variará de 1 a 6, visto que mxn = 6.

• Exemplo 3: suponha que você queira criar 12 figuras e dispô-las em 4 linhas e 3 colunas. Neste caso, m = 4, n = 3 e p variará de 1 a 12, visto que mxn = 12.

Cada plotagem possui seu eixo independentemente da outra.

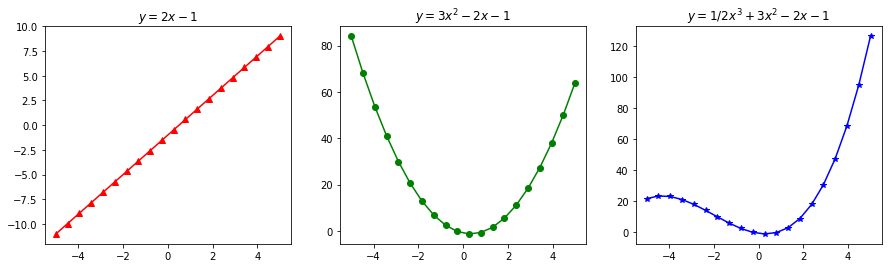
Exemplo 1: gráfico de 1 reta, 1 parábola e 1 polinômio cúbico lado a lado.

x = np.linspace(-5,5,20)

plt.figure(figsize=(15,4))

# aqui p = 1
plt.subplot(1,3,1) # plt.subplot(131) também é válida
plt.plot(x,2*x-1,c='r',marker='^')
plt.title('$y=2x-1$')

# aqui p = 2
plt.subplot(1,3,2) # plt.subplot(132) também é válida
plt.plot(x,3*x**2 - 2*x - 1,c='g',marker='o')
plt.title('$y=3x^2 - 2x - 1$')

# aqui p = 3
plt.subplot(1,3,3) # plt.subplot(133) também é válida
plt.plot(x,1/2*x**3 + 3*x**2 - 2*x - 1,c='b',marker='*')
plt.title('$y=1/2x^3 + 3x^2 - 2x - 1$');

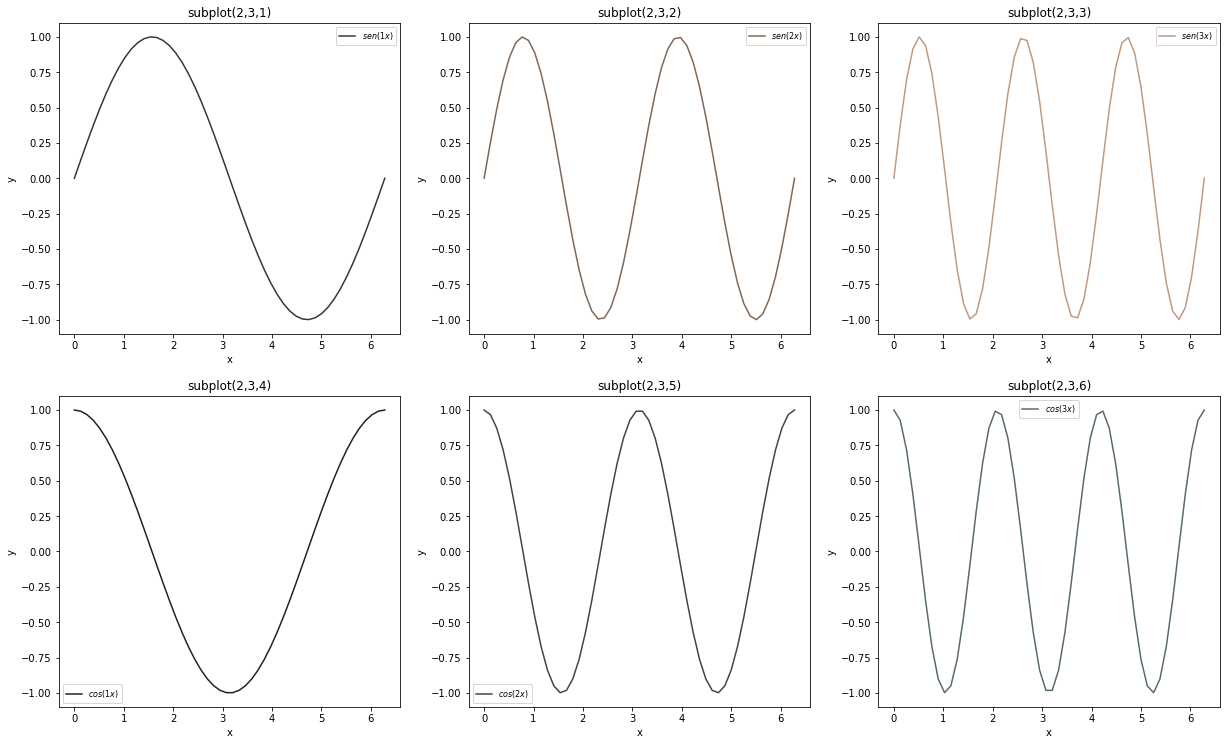
Exemplo 2: gráficos de {\(sen(x)\), \(sen(2x)\), \(sen(3x)\)} e {\(cos(x)\), \(cos(2x)\), \(cos(3x)\)} dispostos em matriz 2x3.

plt.figure(figsize=(15,4))
plt.subplots_adjust(top=2.5,right=1.2) # ajusta a separação dos plots individuais

def sencosx(p):
    x = np.linspace(0,2*np.pi,50)    
    plt.subplot(2,3,p)
    if p <= 3:            
        plt.plot(x,np.sin(p*x),c=[p/4,p/5,p/6],label=f'$sen({p}x)$')
        plt.title(f'subplot(2,3,{p})');
    else:        
        plt.title(f'subplot(2,3,{p})');
        p-=3 # 
        plt.plot(x,np.cos(p*x),c=[p/9,p/7,p/8],label=f'$cos({p}x)$')
    
    plt.legend(loc=0,fontsize=8)
    plt.xlabel('x'); plt.ylabel('y'); 
        
# plotagem     
for p in range(1,7):
    sencosx(p)

Exemplo 3: gráficos de um ponto isolado em matriz 4 x 3.

plt.figure(figsize=(15,4))
m,n = 4,3
def star(p):
    plt.subplot(m,n,p)
    plt.axis('off') # desliga eixos
    plt.plot(0.5,0.5,marker='*',c=list(np.random.rand(3)),ms=p*2)
    plt.annotate(f'subplot({m},{n},{p})',(0.5,0.5),c='g',fontsize=10)
    
for p in range(1,m*n+1):
    star(p);

Plots com gradeado

Podemos habilitar o gradeado usando grid(b,which,axis).

Para especificar o gradeado:

• em ambos os eixos, use b='True' ou b='False'.

• maior, menor ou ambos, use which='major', which='minor' ou which='both'.

• nos eixos x, y ou ambos, use axis='x', axis='y' ou axis='both'.

x = np.linspace(-10,10)
plt.plot(x,x)
plt.grid(True)

plt.plot(x,x)
plt.grid(True,which='major',axis='x')

plt.plot(x,x)
plt.grid(True,which='major',axis='y')

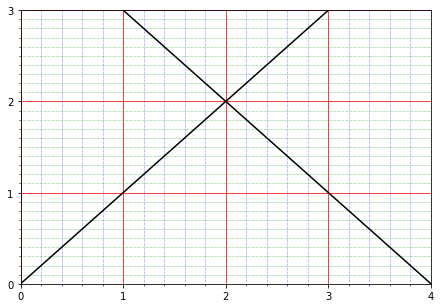
Exemplo: plotagem de gradeado.

Neste exemplo, um eixo abstrato é adicionado sobre a figura (criada diretamente) origem no ponto (0.025,0.025), largura 0.95 e altura 0.95.

ax = plt.axes([0.025, 0.025, 0.95, 0.95])
ax.set_xlim(0,4)
ax.set_ylim(0,3)

# MultipleLocator estabelece pontos de referência para divisão da grade
ax.xaxis.set_major_locator(plt.MultipleLocator(1.0)) # divisor maior em X
ax.xaxis.set_minor_locator(plt.MultipleLocator(0.2)) # divisor maior em X
ax.yaxis.set_major_locator(plt.MultipleLocator(1.0)) # divisor maior em Y
ax.yaxis.set_minor_locator(plt.MultipleLocator(0.1)) # divisor maior em Y

# propriedades das linhas
ax.grid(which='major', axis='x', linewidth=0.75, linestyle='-', color='r')
ax.grid(which='minor', axis='x', linewidth=0.5, linestyle=':', color='b')
ax.grid(which='major', axis='y', linewidth=0.75, linestyle='-', color='r')
ax.grid(which='minor', axis='y', linewidth=0.5, linestyle=':', color='g')

# para remover as ticks, adicione comentários
#ax.set_xticklabels([])
#ax.set_yticklabels([]);

plt.plot(x,x,'k')
plt.plot(x,-x+4,'k')

[<matplotlib.lines.Line2D at 0x7fc4adc1b668>]

Plots com preenchimento

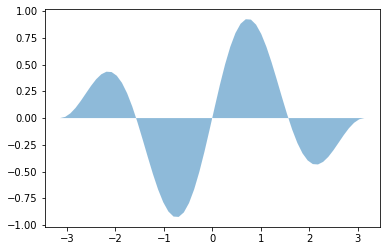
Podemos usar fill_between para criar preenchimentos de área em gráficos.

x = np.linspace(-np.pi, np.pi, 60)
y = np.sin(2*x)*np.cos(x/2)

plt.fill_between(x,y,alpha=0.5);

x = np.linspace(-np.pi, np.pi, 60)
f1 = np.sin(2*x)
f2 = 0.5*np.sin(2*x)

plt.plot(x,f1,c='r');
plt.plot(x,f2,c='k');
plt.fill_between(x,f1,f2,color='g',alpha=0.2);

Computação vetorizada com numpy Tópicos complementares sobre o numpy