7. Lounge das Representações Visuais

Neste capítulo, faremos uma aproximação às diversas classes de representações visuais disponíveis em visualização de dados sem explorar ainda as tecnicalidades de construção gráfica, parcela que será coberta no próximo módulo do curso. O nome lounge é sugestivo, pois será onde teremos um encontro casual com diversas espécies de plots que são cotidianamente aplicados para representar dados econômicos, científicos, sociais, industriais, entre outros.

O propósito será compreender a finalidade e a aplicabilidade dos plots. Organizaremos nosso lounge nos seguintes grupos de visualização:

• quantidades;

• distribuições;

• proporções;

• correlações;

• dados geoespaciais; e

• incertezas.

7.1. Plots para visualizar quantidades

Plots para quantidades são naturalmente ligados a valores numéricos associados a algumas categorias. Neste grupo encontram-se os seguintes gráficos:

• barras, simples, empilhadas (stacked) ou agrupadas (grouped), dispostas horizontal ou verticalmente;

• pontos, uma versão simplificada dos gráficos de barras;

• mapas de calor (heatmap), que quantificam a informação pela cor;

7.1.1. Barras (bar plot)

Para explorar as possibilidades com gráficos de barras e verificar quando eles são ou não adequados, partiremos de uma fonte de dados relativos ao cinema. Os dataframes a seguir registram as 10 maiores bilheterias do cinema nos Estados Unidos e no Brasil, em milhões de dólares, de acordo com o website Box Office Mojo. Os títulos aparecem conforme veiculados no Brasil.

	Filme	Bilheteria (M US$)
0	Top Gun: Maverick	718.3
1	Pantera Negra: Wakanda para Sempre	436.5
2	Doutor Estranho no Multiverso da Loucura	411.3
3	Avatar: O Caminho da Água	401.0
4	Jurassic World: Domínio	376.8
5	Minions 2: A Origem de Gru	369.6
6	Batman	369.3
7	Thor: Amor e Trovão	343.2
8	Homem Aranha: Sem Volta para Casa	231.8
9	Sonic 2: O Filme	190.8

	Filme	Bilheteria (M US$)
0	Homem Aranha: Sem Volta para Casa	56.4
1	Doutor Estranho no Multiverso da Loucura	33.7
2	Avatar: O Caminho da Água	31.4
3	Thor: Amor e Trovão	23.1
4	Minions 2: A Origem de Gru	22.8
5	Batman	22.7
6	Top Gun: Maverick	22.2
7	Pantera Negra: Wakanda para Sempre	21.2
8	Jurassic World: Domínio	15.4
9	Adão Negro	15.3

7.1.1.1. Barras simples (bar plot)

A maneira mais direta de comparar esses números é plotando um gráfico de barras. Vamos testar a disposição vertical.

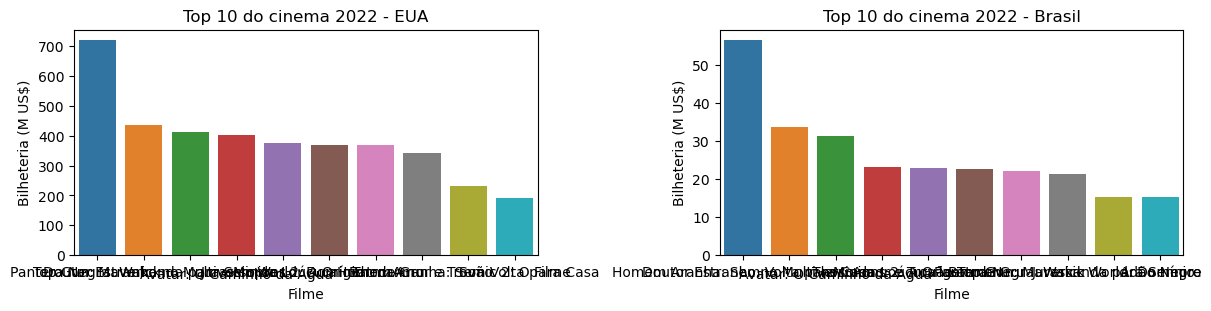
Porém, a pergunta é: quais são os filmes?! Como vemos, a identificação dos nomes dos filmes está prejudicada porque são legendas longas. Vamos testar com rotação.

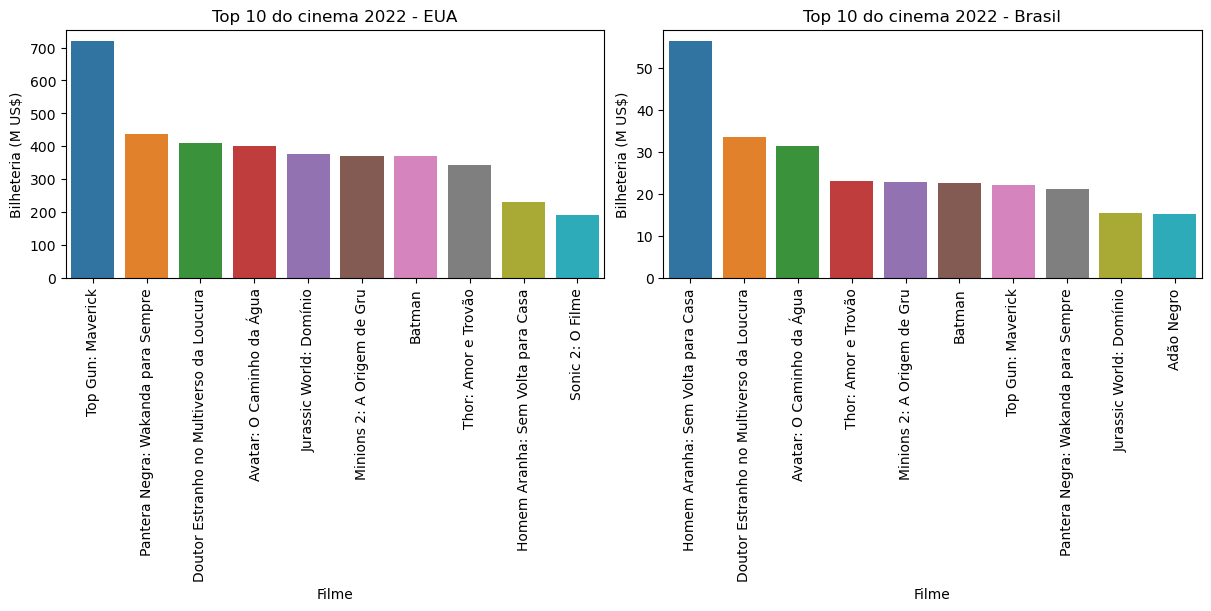
O visual não parece bom porque os nomes ainda são difíceis de ler. Vamos tentar com barras horizontais.

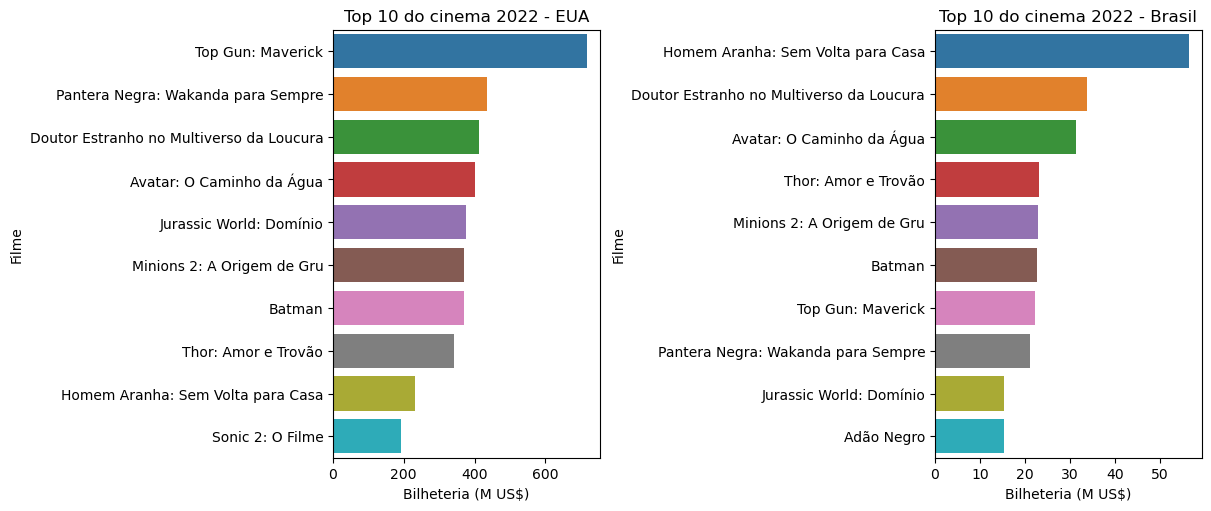
Com as barras horizontais, os nomes dos filmes são melhor identificáveis. Porém, há uma série de melhorias ainda a fazer neste visual. Vamos discuti-las posteriormente.

7.1.1.2. Barras agrupadas (grouped bar plot)

Enquanto as barras simples são capazes de mostrar como quantidades variam em relação a apenas uma categoria, as barras agrupadas são capazes de mostrar variação de quantidades em mais do que uma categoria. No exemplo anterior, a categoria única era o nome dos filmes. Agora, vamos criar um gráfico de barras agrupadas colocando lado a lado os filmes do TOP 10 internacional que também estiveram entre os TOP 10 do Brasil e criar uma categorização baseada na localização geográfica.

Primeiramente, vamos localizar os filmes intersectantes.

	Filme	Bilheteria (M US$)_x	Bilheteria (M US$)_y
0	Top Gun: Maverick	718.3	22.2
1	Pantera Negra: Wakanda para Sempre	436.5	21.2
2	Doutor Estranho no Multiverso da Loucura	411.3	33.7
3	Avatar: O Caminho da Água	401.0	31.4
4	Jurassic World: Domínio	376.8	15.4
5	Minions 2: A Origem de Gru	369.6	22.8
6	Batman	369.3	22.7
7	Thor: Amor e Trovão	343.2	23.1
8	Homem Aranha: Sem Volta para Casa	231.8	56.4

Em seguida, vamos converter os valores das bilheterias em dólares para reais utilizando a taxa de câmbio PTAX 1:5.2171 (dezembro de 2022) e renomear as variáveis de dados.

	Filme	Bilheteria - BR	Bilheteria - US
0	Top Gun: Maverick	115.81962	3747.44293
1	Pantera Negra: Wakanda para Sempre	110.60252	2277.26415
2	Doutor Estranho no Multiverso da Loucura	175.81627	2145.79323
3	Avatar: O Caminho da Água	163.81694	2092.05710
4	Jurassic World: Domínio	80.34334	1965.80328
5	Minions 2: A Origem de Gru	118.94988	1928.24016
6	Batman	118.42817	1926.67503
7	Thor: Amor e Trovão	120.51501	1790.50872
8	Homem Aranha: Sem Volta para Casa	294.24444	1209.32378

Em seguida, manipularemos os nossos dados para identificar cada filme e seu valor pela categoria “Local”.

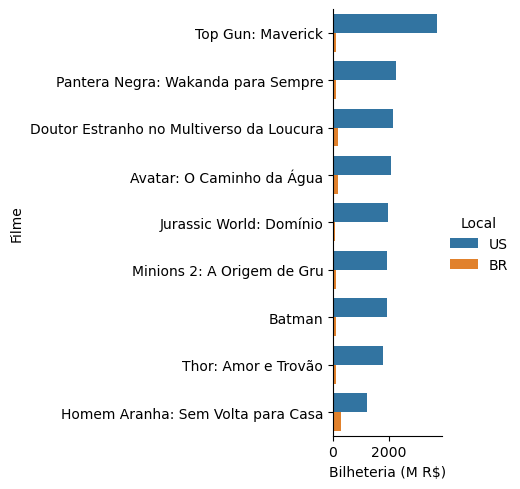
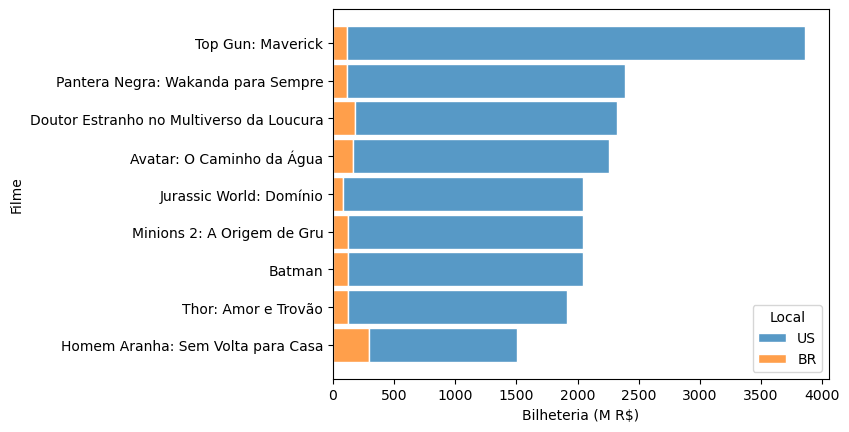
7.1.1.3. Barras empilhadas (stacked bar plot)

Barras empilhadas são adequadas para visualizar quantidades que produzem um total significativo a partir de parcelas que exibem, com clareza, suas proporções para este todo. No exemplo a seguir, procuramos mostrar o peso das bilheterias dos filmes assistidos no Brasil comparado ao peso das bilheterias dos filmes assistidos nos Estados Unidos. Isto é, cada barra representa a soma, em reais, angariada por cada filme nos dois países e cada segmento as parcelas desta soma por localidade. Como se vê, a bilheteria americana é consideravelmente maior do que a brasileira em todos os filmes. Entretanto, percebemos que a ordem de preferência do público americano não se equiparou a da audiência brasileira.

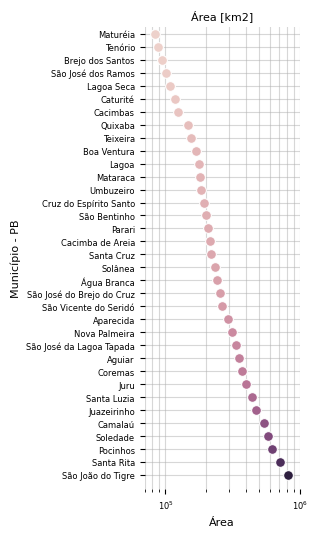
7.1.2. Pontos (dot plot)

O plot de pontos simplifica a escala representada visualmente por gráficos de barra. A posição do ponto marca a quantidade expressa no eixo correspondente. Vimos um exemplo aplicado deste gráfico na Seção 6.1.1.2.7. Na representação abaixo, utilizamos a mesma fonte de dados para plotar as áreas de uma amostra de 35 municípios. A escala logarítmica permite que tenhamos uma visão ampla da extensão em quilômetros quadrados por meio de potências de 10.

7.1.3. Mapas de calor (heatmap)

Alternativamente às representações visuais quantitativas criadas por barras, podemos utilizar os chamados mapas de calor, que permite mapear valores em cores. Utilizaremos um mapa de calor para quantificar visualmente dados sobre crimes violentos.

No dataframe abaixo estão os resultados de uma pesquisa sobre Crimes Violentos Letais Intencionais (CVLI) cometidos em João Pessoa entre 2015 e 2018 (Dados disponíveis aqui). Em particular, constam nele a prevalência dos crimes além das tipologias de armas utilizadas entre 2015 e o primeiro semestre de 2019.

A prevalência permite compreender o quanto é comum, ou rara, uma determinada ocorrência ou situação numa população. A prevalência \(p\) é dada pela equação

\[p = \dfrac{T}{P} \times 1000,\]

onde \(T\) é a quantidade de casos registrados de CVLI e \(P\) a população de um determinado bairro.

	Bairros	Prevalência	Arma de fogo	Arma branca	Outros	Total de casos
0	Varadouro	15.05	44	8	4	56
1	Centro	12.34	27	14	4	45
2	Mandacaru	5.72	64	5	3	72
3	Grotão	5.68	31	4	0	35
4	Bairro das Indústrias	5.51	46	2	0	48
5	Costa do Sol	4.44	26	6	5	37
6	Distrito Industrial	4.24	5	3	0	8
7	Penha	3.89	3	0	1	3
8	Ilha do Bispo	3.63	26	1	2	29
9	Costa e Silva	3.53	24	3	1	29
10	Roger	3.47	26	5	5	36
11	Gramame	3.14	70	8	5	81
12	Varjão	3.18	49	2	3	54
13	Trincheiras	3.15	13	4	5	22
14	Padre Zé	2.02	20	0	1	21
15	Mangabeira	1.65	109	15	2	126

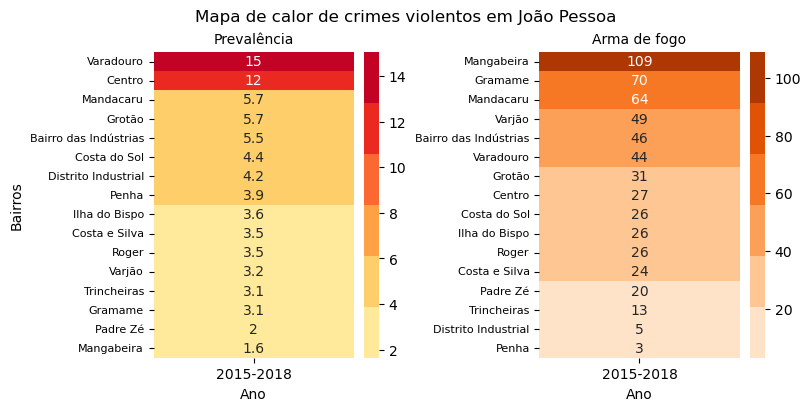
Manipulando os dataframe, conseguimos gerar dois mapas de calor de coluna única, visto que os dados temporais originais agregam os registros entre 2015 e 2018. O primeiro mapa gera uma escala de cor sequencial para a prevalência, ao passo que o segundo mapa faz o mesmo para a quantidade de crimes realizados com arma de fogo.

A partir do que vemos, é imediata a identificação dos bairros de maior/menor prevalência e de crimes com porte de arma de fogo.

	Bairros	Prevalência	Arma de fogo	Arma branca	Outros	Total de casos	Ano
0	Varadouro	15.05	44	8	4	56	2015-2018
1	Centro	12.34	27	14	4	45	2015-2018
2	Mandacaru	5.72	64	5	3	72	2015-2018
3	Grotão	5.68	31	4	0	35	2015-2018
4	Bairro das Indústrias	5.51	46	2	0	48	2015-2018
5	Costa do Sol	4.44	26	6	5	37	2015-2018
6	Distrito Industrial	4.24	5	3	0	8	2015-2018
7	Penha	3.89	3	0	1	3	2015-2018
8	Ilha do Bispo	3.63	26	1	2	29	2015-2018
9	Costa e Silva	3.53	24	3	1	29	2015-2018
10	Roger	3.47	26	5	5	36	2015-2018
12	Varjão	3.18	49	2	3	54	2015-2018
13	Trincheiras	3.15	13	4	5	22	2015-2018
11	Gramame	3.14	70	8	5	81	2015-2018
14	Padre Zé	2.02	20	0	1	21	2015-2018
15	Mangabeira	1.65	109	15	2	126	2015-2018

7.2. Plots para visualizar distribuições

A estatística descritiva é limitada para resumir dados, visto que dados com características completamente distintas podem ter os mesmos valores para média, mediana e variância, por exemplo. Uma forma aprofundada de reconhecer as características dos dados é inspecionar a sua distribuição. No grupo das distribuições, consideraremos os seguintes plots:

• histogramas, com intervalo de classes uniforme;

• densidades, incluindo densidade simples;

• cumulativos, incluindo densidade cumulativa empírica;

• quantis, abrangendo o quantil-quantil (QQ-plot);

A fim de criar as primeiras representações visuais para este grupo, usaremos dados estatísticos reais concernentes a ànalise de um processo de moldagem em uma linha de produção de uma indústria química do Rio Grande do Sul. O propósito da análise era investigar inconsistências do processo. A tabela a seguir registra massas de amostras extraídas de duas matrizes (2 e 7) ao longo de três dias a cada 30 minutos no período compreendido entre 07:00h e 13:00h ([Saldanha et al., 2013]).

	Horário	Peso (g)	Dia	Matriz
0	07:00	39.2	1	2
1	07:30	39.4	1	2
2	08:00	39.7	1	2
3	08:30	39.2	1	2
4	09:00	39.6	1	2
...	...	...	...	...
73	11:00	39.8	3	7
74	11:30	40.2	3	7
75	12:00	40.3	3	7
76	12:30	39.9	3	7
77	13:00	40.4	3	7

78 rows × 4 columns

7.2.1. Histograma

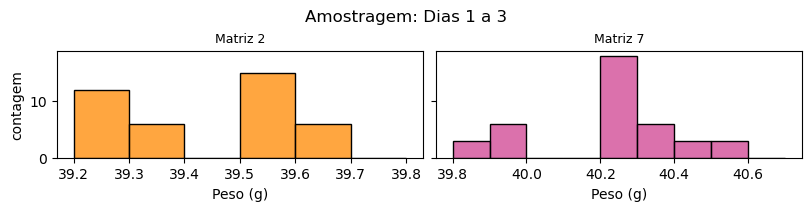
O histograma é a representação visual mais comumemente empregada para retratar distribuições. O gráfico é composto de retângulos preenchidos cujas alturas correspondem às frequências de observação de determinados valores que compreendem um intervalo de classe.

Na figura a seguir plotamos histogramas para as massas dos produtos processados em cada uma das matrizes. Por brevidade, consideramos no histograma todos os valores registrados ao longo dos 3 dias. Observamos que há lacunas nos histogramas pela ausência de massas reportadas nas respectivas massas.

7.2.2. Densidade simples

Plots de densidade simples são versões contínuas dos histogramas e vem ganhando popularidade devido à facilitação de sua construção por ferramentas computacionais modernas. Nesses gráficos, a frequência das quantidades é representada por uma curva suave que, na verdade, é uma aproximação da distribuição de probabilidade fundamental que explica o comportamento real – a qual é desconhecida. Tem sido frequente a estimativa da curva de densidade pela técnica dos estimadores de núcleo (kernel density estimator, ou simplesmente, KDE).

A metodologia do KDE recompõe a curva contínua através da mistura (combinação) de várias funções conhecidas como “núcleos” (kernels) que são abertos em torno de cada ponto amostrado dentro de uma largura de banda predefinida. Há diversos tipos de kernel possíveis de se trabalhar, tais como exponencial, linear, epanechnikov e o mais popular de todos, o gaussiano.

Abaixo, fazemos plotagens da densidade de distribuição para cada matriz da indústria. O último plot contém as duas distribuições. Vê-se que a curva “imita” o comportamento já visualizado no gráfico.

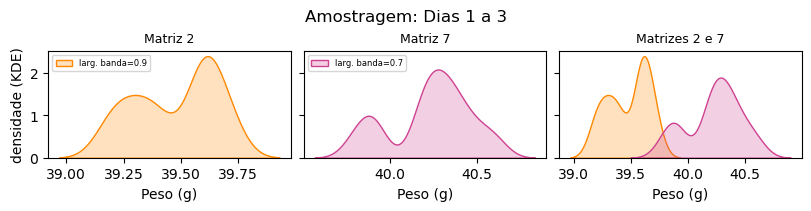
No próximo exemplo, plotamos os histogramas juntamente com a curva estimada por KDE.

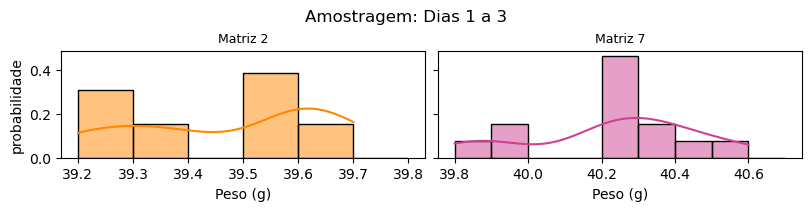
7.2.3. Densidade cumulativa

Histogramas e plots de densidade possuem o revés de dependerem de parâmetros que são escolhidos pelo usuário, tais como o número de intervalos de classe (bins, ou bin widths) e a largura de banda. Pelo fato de que eles podem ser livremente alterados, esses gráficos tornam-se mais uma interpretação dos dados do que uma visualização direta deles. A desvantagem é que eles são menos intuitivos.

Opostamente, plots de densidade simplesmente mostram os dados de uma só vez, sem uso de parâmetros. Para entender minimamente o conceito de densidade cumulativa, ou também de densidade cumulativa empírica (representada pelo acrônimo ECDF), usaremos um rol de dados que contém a nota auferida por estudantes de uma classe de Engenharia formada por 60 pessoas na primeira avaliação. A tabela pode ser encontrada a seguir.

	Estudante	Nota
0	1	4.7
1	2	6.9
2	3	7.1
3	4	7.0
4	5	5.2
5	6	7.8
6	7	7.2
7	8	5.2
8	9	6.6
9	10	4.1
10	11	8.1
11	12	6.4
12	13	8.1
13	14	7.8
14	15	5.6
15	16	7.1
16	17	3.4
17	18	7.2
18	19	6.9
19	20	7.0
20	21	6.4
21	22	2.7
22	23	3.5
23	24	4.5
24	25	7.3
25	26	7.2
26	27	7.6
27	28	8.4
28	29	8.0
29	30	7.9
30	31	7.2
31	32	7.7
32	33	7.0
33	34	9.1
34	35	9.0
35	36	8.4
36	37	8.1
37	38	7.2
38	39	6.7
39	40	8.0
40	41	5.2
41	42	6.3
42	43	7.4
43	44	4.5
44	45	7.9
45	46	7.9
46	47	2.1
47	48	7.1
48	49	8.2
49	50	9.8
50	51	10.0
51	52	8.3
52	53	7.2
53	54	4.1
54	55	8.3
55	56	7.0
56	57	7.3
57	58	6.4
58	59	7.3
59	60	9.5

A distribuição cumulativa é uma representação visual que fornece dois caminhos de compreensão para os dados quantitativos em análise.

Em primeiro lugar, sob o ponto de vista de contagem. Neste caso particular, a nota de cada estudante é disposta no eixo horizontal, enquanto que no eixo vertical consta um “ranqueamento ascendente” de estudantes. A curva cresce cumulativamente daquele(a) estudante que possui a nota mais baixa (ranqueamento 1) até o(a) estudante que possui a maior nota (ranqueamento 60).

Em segundo lugar, sob o ponto de vista de proporção. Neste caso particular, a nota de cada estudante é disposta no eixo horizontal, enquanto que no eixo vertical consta a proporção de estudantes que atingiram determinada nota. A curva é idêntica, mas podemos verificar rapidamente o ranqueamento por percentuais. Por exemplo, o gráfico mostra que em torno de 25% da turma conseguiu nota, no máximo de 6,0.

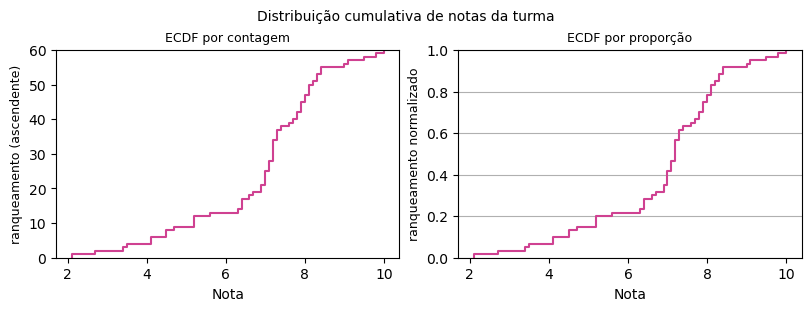
7.2.4. Quantis

Quantis são uma espécie de “ranqueamento” dos dados. Quando divididos em frações de 100, são chamados de percentis. Um jogador de futebol avaliado estatisticamete com percentil de 86%, por exemplo, indicaria que ele está entre os 14% melhores jogadores de futebol. Quantis então servem para dividir os dados ordenados em subconjuntos.

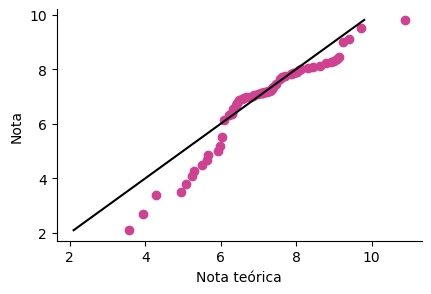
O plot chamado de quantil-quantil, ou QQ plot, é bastante utilizado para testar se os dados observados seguem uma determinada distribuição teórica. Quando a distribuição teórica é a normal, chamamos o gráfico de plot de probabilidades normal (veja também similaridades com o plot de probabilidades, PP-plot).

Um QQ-plot é um plot de pontos. Geralmente, coloca-se uma reta de referência. Quando os pontos desviam-se desta reta, os dados observados supostamente seguem uma distribuição que não coincide com a teórica. Em geral, é quase impossível atingir tal coincidência.

Para QQ-plots, deveremos instalar o módulo seaborn-qqplot utilizando pip para acessar a função pplot. Este módulo é uma extensão do seaborn.

Feitos esses passos, conseguimos gerar o seguinte gráfico de teste.

7.3. Plots para visualizar proporções

A visualização de proporções deve levar em conta projetos gráficos que sejam capazes de mostrar como algum grupo, entitade ou quantidade pode ser “quebrada” em partes menores, assim constituindo uma proporção do todo. Classicamente, o gráfico de “torta” (pie chart) é o mais tradicionalmente aplicado quando o interesse é visualizar proporções. Entretanto, muitos profissionais criticam seu uso exagerado.

Torna-se complicado interpretar gráficos de torta quando ele possui “fatias” excessivas. Por outro lado, quando ele é dividido em poucas partes, seu uso é recomendado. A polêmica em torno deste gráfico não é puramente nociva. Ela apenas ressalta a inexistência de representações “ótimas” para proporções. De fato, neste grupo de plotagem, não faremos uma separação explícita sobre os estilos, mas consideraremos uma miscelânea de plots, tanto inspirados na estrutura de outros grupos, mas adequados para representar proporções, quanto mais genéricos, que incorporam mosaicos, árvores estruturadas (treemap), diagramas de Venn, donut, dendrogramas e raios de sol (sunburst).

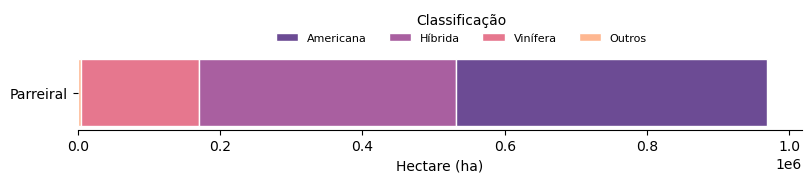
7.3.1. Barras

Podemos visualizar proporções diretamente a partir de gráficos de barras. Usaremos dados do SIVIBE/MAPA sobre vinhos e bebidas para exemplos. (Nota: para operacionalizar planilhas do Excel, poderá ser necessária a instalação do módulo openpyxl).

Abaixo fazemos

	Código propriedade	Classificação	Área Parreiral (calc) ha
0	1717411	Vinífera	14644.128633
1	1715835	Vinífera	2085.518510
2	1712357	Híbrida	12.548700
3	1712357	Vinífera	1832.432534
4	1712721	Americana	13.185600
...	...	...	...
41407	1731195	Híbrida	2.240000
41408	1731050	Americana	0.000000
41409	1730884	Vinífera	5.792904
41410	1730188	Híbrida	0.000000
41411	1729179	Híbrida	4.024428

41412 rows × 3 columns

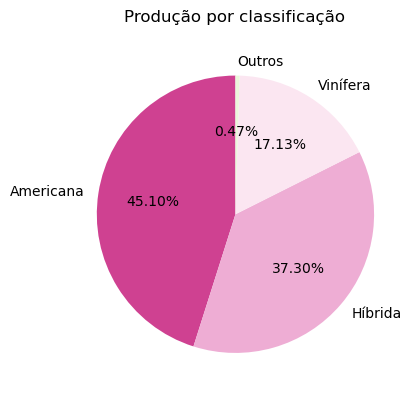
7.3.2. Fatias

7.3.3. Diagrama de Venn

Vamos fazer um comparativo de um grupo de artistas que apenas cantam, apenas atuam ou cantam e atuam. A tabela está disposta a seguir:

	Artista	Canta	Atua
0	Marisa Orth	sim	sim
1	Preta Gil	sim	sim
2	Clarice Falcão	sim	sim
3	Mariana Rios	sim	sim
4	Marjorie Estiano	sim	sim
5	Alexandre Nero	sim	sim
6	Chay Suede	sim	sim
7	Fiuk	sim	sim
8	Fábio Jr.	sim	sim
9	Evandro Mesquita	sim	sim
10	Seu Jorge	sim	sim
11	Djavan	sim	não
12	Lenine	sim	não
13	Wesley Safadão	sim	não
14	Ana Carolina	sim	não
15	Marisa Monte	sim	não
16	Milton Nascimento	sim	não
17	Bruno Gagliasso	não	sim
18	Osmar Prado	não	sim
19	Luana Piovani	não	sim
20	Caio Blat	não	sim
21	Caio Castro	não	sim
22	Rodrigo Lombardi	não	sim
23	Fernanda Montenegro	não	sim

Para plotar diagramas de Venn, é necessário instalar o módulo matplotlib_venn (use pip). Na representação simples abaixo, temos os conjuntos variando o diâmetro em função da cardinalidade de seus elementos.

7.3.4. Árvore estruturada

O diagrama de árvore estruturada (treemap) permite seccionar um todo em áreas representativas, como mostramos na apresentação deste curso. O treemap abaixo exibe o conteúdo deste curso em termos de quadros de tamanhos que variam em função da carga horária aproximada dos módulos e avaliações.

7.4. Plots para visualizar correlações

Correlação é qualquer associação estatística entre um par de variáveis. Quanto mais correlacionadas estão duas variáveis, mais “alinhamento” há entre elas. Isto é, uma análise de correlação fornece um número que resume o grau de relacionamento linear entre duas variáveis. Introduziremos este assunto com alguns conceitos fundamentais.

Podemos interpretar a correlação também pelo ponto de vista de “dependência linear”. Duas variáveis perfeitamente correlacionadas são similares a dois vetores paralelos, ou seja, linearmente dependentes. Por outro lado, duas variáveis totalmente não correlacionadas são similares a dois vetores perpendiculares, ou seja, linearmente independentes.

Neste grupo também não apresentaremos uma divisão enfática dos tipos de representações dada a sua variedade. Estão incluídos aqui os seguintes plots:

• dispersão (scatter plot), bolhas (bubble chart), inclinação (slopegraph), linhas;

• contornos de densidade, classes 2D (2D bins), classes hexagonais (hex bins);

• correlograma.

Para grandes dados, plots de dispersão tornam-se pouco informativos devido ao emaranhado de pontos. Em um cenário como este, são preferíveis os plots de contornos e classes. Para mais do que duas quantidades, correlogramas são recomendados.

Discutiremos apenas alguns exemplos.

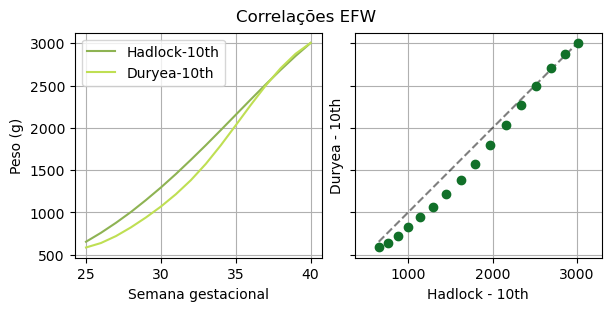
7.4.1. Dispersão

Este exemplo investiga a dispersão existente entre dois métodos que explicam o crescimento fetal em função da semana gestacional. O gráfico à esquerda mostra a curva de Hadlock e de Duryea, ambas para o percentil 10. À direita, plotamos o gráfico de dispersão entre ambas as curvas para saber como elas se correlacionam. A existência de uma “barriga” abaixo da linha pontilhada mostra que elas, de fato, são diferentes, embora possuam uma tendência equivalente. Caso todos os pontos verdes estivessem sobre a reta tracejada, diríamos que elas seriam idênticas. Ou seja, a dispersão é baixa.

7.5. Plots para visualizar dados geoespaciais

Dados geoespaciais são melhor dispostos através de mapas que projetam coordenadas do globo terrestre em superfícies planas. Geralmente, os mapas seguem o formato e as fronteiras de territórios. Neste grupo encontram-se:

• coropletas, ou mapas coropléticos (choropleth), que colorem regiões do mapa para realizar associações com quantidades ou categorias.

• cartogramas, que se constituem em representações distorcidas ou simplificadas das regiões. Por exemplo, associar estados da federação a formas retangulares menores arranjadas sobre uma forma poligonal maior próxima ao formato do Brasil.

O exemplo a seguir é uma coropleta para a população brasileira segundo dados do IBGE para o Censo 2022. Os valores são exibidos na tabela.

/Users/gustavo/opt/anaconda3/envs/dataviz/lib/python3.9/site-packages/geopandas/plotting.py:48: ShapelyDeprecationWarning: The 'type' attribute is deprecated, and will be removed in the future. You can use the 'geom_type' attribute instead.
  if geom is not None and geom.type.startswith(prefix) and not geom.is_empty:

pop

	UF	Pop 2022	geometry
0	Acre	830018.0	POLYGON ((-68.10553 -10.72192, -68.10547 -10.7...
1	Alagoas	3127683.0	MULTIPOLYGON (((-35.88986 -9.84431, -35.88986 ...
2	Amapá	733759.0	MULTIPOLYGON (((-50.82570 2.52208, -50.82570 2...
3	Amazonas	3941613.0	POLYGON ((-58.13699 -7.35614, -58.13682 -7.356...
4	Bahia	14141626.0	MULTIPOLYGON (((-38.69208 -17.95958, -38.69208...
5	Ceará	8794957.0	MULTIPOLYGON (((-40.83181 -2.88125, -40.83181 ...
6	Distrito Federal	2817381.0	POLYGON ((-47.93915 -16.05135, -48.02110 -16.0...
7	Espírito Santo	3833712.0	MULTIPOLYGON (((-40.88403 -21.16125, -40.88403...
8	Goiás	7056495.0	POLYGON ((-49.00480 -18.53718, -49.01248 -18.5...
9	Maranhão	6776699.0	MULTIPOLYGON (((-44.54986 -1.88458, -44.54986 ...
10	Mato Grosso	3658649.0	POLYGON ((-52.47143 -16.12672, -52.48842 -16.1...
11	Mato Grosso do Sul	2757013.0	POLYGON ((-54.16836 -23.99920, -54.17063 -24.0...
12	Minas Gerais	20539989.0	POLYGON ((-50.84402 -19.96758, -50.85332 -19.9...
13	Paraná	11444380.0	MULTIPOLYGON (((-48.36514 -25.73403, -48.36514...
14	Paraíba	3974687.0	MULTIPOLYGON (((-43.01208 -9.40801, -43.01453 ...
15	Pará	8120131.0	MULTIPOLYGON (((-47.29792 -0.63375, -47.29792 ...
16	Pernambuco	9058931.0	MULTIPOLYGON (((-35.13597 -8.83792, -35.13597 ...
17	Piauí	3271199.0	POLYGON ((-42.69078 -9.54547, -42.69122 -9.545...
18	Rio Grande do Norte	3302729.0	MULTIPOLYGON (((-35.10958 -6.19375, -35.10958 ...
19	Rio Grande do Sul	10882965.0	MULTIPOLYGON (((-52.07069 -32.02847, -52.07069...
20	Rio de Janeiro	16055174.0	MULTIPOLYGON (((-44.67125 -23.35458, -44.67125...
21	Rondônia	1581196.0	POLYGON ((-62.89219 -12.86014, -62.89212 -12.8...
22	Roraima	636707.0	POLYGON ((-60.03790 0.26349, -60.04676 0.23211...
23	Santa Catarina	7610361.0	MULTIPOLYGON (((-48.54236 -27.93180, -48.54236...
24	Sergipe	2210004.0	MULTIPOLYGON (((-37.38458 -11.45986, -37.38458...
25	São Paulo	44411238.0	MULTIPOLYGON (((-48.08236 -25.28431, -48.08236...
26	Tocantins	1511460.0	POLYGON ((-49.23736 -12.88397, -49.23532 -12.8...

7.6. Plots para visualizar incertezas

Incertezas são inerentes a medições experimentais e laboratoriais, bem como a cálculos que envolvem estimativas e previsões sobre ocorrências futuras. Geralmente, incertezas são representadas por barras ou áreas que se estendem em torno de um ponto ou linha de referência. Neste grupo, incluem-se os plots acompanhados de barras de erro de intervalos de confiança.

7.7. Referências

SRB+13

Paulo Saldanha, Carolina Kirsch Rothe, Fabiana Regina Benedett, Diego Augusto de Jesus Pacheco, Carlos Fernando Jung, and Carla Scwenberg TEN CATEN. Analisando a aplicação do controle estatístico de processos na indústria química: um estudo de caso. Espacios (Caracas), 34:1–18, 2013.