Cores
Contents
6. Cores#
Cores são constituintes fundamentais da aparência das representações visuais. Com elas, conseguimos enaltecer o estímulo visual da audiência e impactar a percepção visual dos espectadores. Variar matizes e colorações traz compreensões àquilo que desejamos mostrar. As cores, por sua vez, podem ser usadas para, principalmente:
distinguir grupos de dados;
representar valores; e
produzir destaques (highlights).
Entretanto, antes de se preocupar com a decoração de nossas representações visuais, é preciso se dedicar ao significado delas [Kirk, 2016].
6.1. Escalas de cor#
Como enunciamos, um dos objetivos de usar cores em visualização de dados é distinguir grupos através da plotagem de dados qualitativos categóricos. Para esta finalidade, podemos usar paletas de cores discretas, também chamadas de escalas de cor qualitativas. Essas paletas são compostas de uma quantidade limitada de cores que produzem uma percepção de “grupos finitos” de informação.
Usando a função seaborn.color_palette(), por exemplo, podemos invocar uma enorme quantidade de escalas de cores qualitativas do próprio módulo, ou qualquer outro mapa de cores predefinido ou mesmo construído por nós. Entenderemos mapas de cores mais à frente.
A seguir, exibimos 3 escalas qualitativas com 6, 10 e 14 cores segundo a paleta padrão.
from seaborn import color_palette
color_palette(n_colors=6)
!open /Users/gustavo/opt/anaconda3/envs/dataviz/lib/python3.9/site-packages/seaborn/palettes.py
color_palette(n_colors=10)
color_palette(n_colors=14)
Observe que neste exemplo de 14 cores, as últimas 4 são as mesmas que as primeiras 4. Isto acontece porque a paleta padrão que estamos utilizando possui apenas 10 cores. Quando solicitamos mais, ela simplesmente entra em um ciclo repetitivo.
A paleta padrão utilizada pelo seaborn, chamada de prop_cycle, é herdada do matplotlib 2.0, quando passou a substituir a paleta circular anterior, baseada em 7 cores: azul, verde, vermelho, ciano, magenta, amarelo e preto (bgrcmyk). As cores da paleta padrão podem ser prontamente obtidas com as seguintes instruções.
from matplotlib import rcParams
for c in rcParams['axes.prop_cycle'].by_key()['color']:
print(c, end = ' ')
#1f77b4 #ff7f0e #2ca02c #d62728 #9467bd #8c564b #e377c2 #7f7f7f #bcbd22 #17becf
A alteração das propriedades “circulares” de cor depende da API cycler, a qual serve para estilizações customizadas. Para maior detalhamento, consulte este link. Para uma apresentação dos motivos por trás da escala padrão, assista este vídeo.
Podemos reduzir as saturações dessas paletas por uma certa proporção para criar cores menos vívidas incorporando o parâmetro desat.
color_palette(n_colors=6,desat=0.1)
color_palette(n_colors=10,desat=0.5)
color_palette(n_colors=14,desat=0.9)
6.1.1. Paletas predefinidas#
O seaborn possui algumas paletas de cores predefinidas que alteram as tonalidades das cores. São elas:
muted;bright;pastel;dark; ecolorblind.
color_palette('muted')
color_palette('bright')
color_palette('pastel')
color_palette('dark')
color_palette('colorblind')
6.1.1.1. Paletas qualitativas#
O matplotlib também possui uma série de paletas de cores. Em particular, as qualitativas são:
Pastel1,Pastel2;Paired,Accent;Dark2;Set1,Set2,Set3;tab10,tab20,tab20b,tab20c.
Cada uma pode ser invocada pela função seaborn.color_palette() naturalmente:
color_palette('Paired',n_colors=10)
color_palette('Set1',n_colors=10)
color_palette('tab20b',n_colors=10)
6.1.1.1.1. Exemplo de aplicação: dado qualitativo categórico#
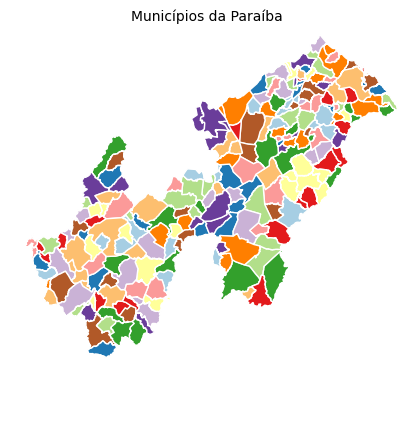
Para um exemplo aplicado, vamos plotar a malha geográfica de municípios do estado da Paraíba usando uma das escalas de cor disponíveis no matplotlib. Definiremos a função plot_municipios_PB(escala); para trabalhar com sistemas de coordenadas existentes no módulo cartopy, a qual gerará uma paleta de 223 cores (uma para cada município) com base na escala escolhida pelo usuário e, em seguida, fará a representação visual dos dados categorizados.
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.io.shapereader as shpreader
from seaborn import color_palette
def plot_municipios_PB(plte):
'''Plota a malha de municípios do estado da Paraíba a partir
de uma escala de cores escolhida pelo usuário.'''
# eixo e projeções
ax = plt.axes([0, 0, .8, .8],projection=ccrs.LambertConformal())
ax.set_extent([-35.5,-38.5,-6,-8.5], ccrs.Geodetic()) # (lat1,lat2,lon1,lon2); cobertura JPA
ax.set_axis_off()
# malha geográfica da PB (IBGE)
# requer diretório de arquivos SHP
# https://www.ibge.gov.br/en/geosciences/territorial-organization/territorial-meshes/18890-municipal-mesh.html?=&t=acesso-ao-produto
shapename = '../data/PB_Municipios_2021/'
shp = shpreader.Reader(shapename)
nmun = len(shp) # no. municípios
# plotagem dos polígonos dos municípios
plt.title('Municípios da Paraíba',fontsize=10)
cols = color_palette(plte,n_colors=nmun) # paleta de 223 cores
for i,s in enumerate(shp.geometries()):
ax.add_geometries([s], ccrs.PlateCarree(),facecolor=cols[i], edgecolor='white');
return shp
# Plotagem com escala de cores escolhida pelo usuário
plot_municipios_PB('Paired');
6.1.1.2. Paletas contínuas e demais paletas predefinidas#
O matplotlib dispõe de outras dezenas de paletas com características diversas. Em particular, paletas contínuas são aquelas que geram uma percepção de continuidade e são bastante úteis para a plotagem de dados quantitativos numéricos e dados onde prevaleça algum ordenamento. As classes de paletas do matplotlib são:
Sequenciais com percepção de uniformidade:
viridis,plasma,inferno,magmaecividisSequenciais do grupo 1:
Greys,Purples,Blues,Greens,Oranges,Reds,YlOrBr,YlOrRd,OrRd,PuRd,RdPu,BuPu,GnBu,PuBu,YlGnBu,PuBuGn,BuGneYlGn;Sequenciais do grupo 2:
binary,gist_yarg,gist_gray,gray,bone,pink,spring,summer,autumn,winter,cool,Wistia,hot,afmhot,gist_heatecopper;Divergentes:
PiYG,PRGn,BrBG,PuOr,RdGy,RdBu,RdYlBu,RdYlGn,Spectral,coolwarm,bwreseismic;Cíclicas:
twilight,twilight_shifted,hsv;Qualitativas: já vistas anteriormente.
Genéricas:
flag,prism,ocean,gist_earth,terrain,gist_stern,gnuplot,gnuplot2,CMRmap,cubehelix,brg,gist_rainbow,rainbow,jet,turbo,nipy_spectralegist_ncar.
Curiosidade
A maioria das escalas de cor admitem uma versão “reversa” obtida adicionando-se o sufixo _r à string que define a escala (cividis_r, hsv_r etc.).
Não é nossa intenção explorar cada uma das paletas aqui, mas mostrar algumas aplicações. É importante notar que a escolha de paletas de cores depende de inúmeros fatores tais como:
natureza dos dados (p.ex. qualitativo, quantitativo, discreto, contínuo);
destaque (p.ex. destacar valor médio e outliers);
intuição (p.ex. tons de verde para tratar parâmetros métricos de sustentabilidade);
necessidades especiais (p.ex. público com particularidades visuais); e
tradição do campo do conhecimento (p.ex. cores binárias em imagens médicas).
Segundo a documentação do matplotlib, as escalas de cor são explicadas da seguinte forma:
Sequenciais: mudanças incrementais na luminosidade e na saturação de cor, muitas vezes usando um único matiz; deve ser usado para representar dados que possuam alguma ordenação.
Divergentes: mudança na luminosidade e possivelmente na saturação de duas cores diferentes que se encontram no meio a uma cor insaturada; deve ser usada quando a informação que está sendo plotada tem um valor médio crítico ou quando os dados se desviam em relação a zero.
Cíclicas: mudança na luminosidade de duas cores diferentes que se encontram no meio e início/fim em uma cor insaturada; deve ser usado para valores relativos a fenômenos cíclicos/periódicos, tais como ângulo de fase, direção do vento ou hora do dia.
Qualitativas: cores diversas; deve ser usada para representar informações que não possuem ordem ou relacionamentos.
A seguir mostramos o visual de algumas dessas escalas:
6.1.1.2.1. Sequenciais com percepção de uniformidade#
color_palette('viridis',n_colors=12)
color_palette('magma',n_colors=12)
6.1.1.2.2. Sequenciais do grupo 1#
color_palette('Oranges',n_colors=12)
color_palette('Blues',n_colors=12)
color_palette('YlOrRd',n_colors=12)
6.1.1.2.3. Sequenciais do grupo 2#
color_palette('bone',n_colors=12)
color_palette('hot',n_colors=12)
color_palette('copper',n_colors=12)
6.1.1.2.4. Divergentes#
color_palette('RdBu',n_colors=12)
color_palette('Spectral',n_colors=12)
color_palette('seismic',n_colors=12)
6.1.1.2.5. Cíclicas#
color_palette('twilight',n_colors=12)
color_palette('twilight_shifted',n_colors=12)
color_palette('hsv',n_colors=12)
6.1.1.2.6. Genéricas#
color_palette('prism',n_colors=12)
color_palette('terrain',n_colors=12)
color_palette('rainbow',n_colors=12)
Curiosidade
Diversos pacotes que lidam com mapas de cores podem ser encontrados (https://matplotlib.org/mpl-third-party/#colormaps-and-styles)[aqui].
6.1.1.2.7. Exemplo aplicado: dado quantitativo numérico#
Neste segundo exemplo aplicado, recuperamos os valores das áreas (em quilômetros quadrados) de todos os municípios do estado da Paraíba a partir dos arquivos de geolocalização e construímos um gráfico de dispersão ordenado. A representação visual mostra a variação do escore padronizado (também conhecido como Fator Z, ou Z-score) das áreas dos municípios. Um Fator Z igual a zero representa a média do conjunto. Valores de Fator Z negativos representam municípios cuja área é menor do que a média do estado; positivos, municípios com área acima da média.
Além disso, escolhemos uma escala de cor divergente que muda a tonalidade consoante variação do Fator Z. Os dados ordenados permitem que detectemos rapidamente os municípios de menor e maior extensão territorial.Observa-se pelo visual que, Bonito de Santa Fé, Mãe D’Água e Araçagi parecem disputar a posição média, mas é evidente que Lucena e Pombal possuem, nesta ordem, a menor e maior variação em relação à média.
from matplotlib.pyplot import subplots
from seaborn import set_palette, lineplot
from scipy.stats import zscore
from pandas import DataFrame
import cartopy.io.shapereader as shpreader
# recupera dados do shapefile
shp = shpreader.Reader('../data/PB_Municipios_2021/')
nmun = len(shp)
CD, NM, AREA = [], [], []
for mun in range(nmun):
CD.append(shp._data[mun]['CD_MUN'])
NM.append(shp._data[mun]['NM_MUN'])
AREA.append(shp._data[mun]['AREA_KM2'])
# converte dados de área para float e cálcula escore padronizado
df = DataFrame({'CD':CD,'NM':NM,'AREA':AREA})
df['AREA'] = df['AREA'].apply(lambda x: float(str(x).replace('.','')))
df['Z'] = zscore(df['AREA'])
df = df.sort_values(by='Z')
# paleta de cores
set_palette("PiYG")
# figura
fig, ax = subplots(1,1,figsize=(1,30),constrained_layout=False)
f = lineplot(data=df,y='NM',x='Z',marker='o',markersize=7,hue="Z",linewidth=0,ax=ax)
# linha média
ax.axvline(x=0,color='#CE408E',lw=1.2,alpha=0.8)
# decoração
ax.axis('equal');
ax.grid(axis='both');
ax.tick_params(axis='both', labelsize=6)
ax.set_xlim(-3.5,3.5);
ax.set_ylim(nmun+0.1,-0.5)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_legend().remove()
ax.set_title('Escore padronizado: área [km2]',fontsize=8)
ax.set_xlabel('Z-score',fontsize=8);
ax.set_ylabel('Município - PB',fontsize=8);

De fato, uma rápida investigação no dataframe permite-nos asseverar o que foi dito sobre Lucena e Pombal e afirmar com mais certeza que Araçagi disputa, na verdade, com Solânea a extensão média, visto que a inflexão do Fator Z ocorre entre as duas localidades.
df['NM'][df['Z'].idxmin()], df['AREA'][df['Z'].idxmin()]
('Lucena', 938.0)
df['NM'][df['Z'].idxmax()], df['AREA'][df['Z'].idxmax()]
('Pombal', 894099.0)
df[(df['Z'] > -0.005) & (df['Z'] < 0.005)]
| CD | NM | AREA | Z | |
|---|---|---|---|---|
| 11 | 2500809 | Araçagi | 232177.0 | -0.003269 |
| 207 | 2516003 | Solânea | 233043.0 | 0.001250 |
6.2. Modelos de cor#
As cores podem ser representadas de forma abstrata através de um modelo matemático baseado em ênuplas geralmente de 3 ou 4 coordenadas. Ou seja, de forma mais geral, uma cor é uma estrutura do tipo \(c = (c_1,c_2,c_3)\), ou \(c = (c_1,c_2,c_3,c_4)\). Quando cada uma das componentes \(c_i\) são associadas a aspectos da percepção visual, elas podem ter diferentes interpretações e dar origens a um espaço de cores. Porém, antes de adentrarmos em particularidades, vamos entender brevemente o aspecto físico das cores e o que, de fato, é uma cor.
6.2.1. Óptica, ondas e cores#
Cor é o nome que damos à qualidade perceptiva da luz, que se dá por uma resposta subjetiva do cérebro quando a retina de nossos olhos é estimulada. A nossa percepção das cores baseia-se em nossa sensibilidade a ondas eletromagnéticas com frequencias distintas que se misturam para produzir respostas em nossos “cones visuais” (células receptoras localizadas na retina). O espectro de energia visível – gráfico de intensidade vs. comprimento de onda (ou frequencia) – é caracterizado por comprimentos de onda na faixa de 400 - 700 nm. Esta faixa de valores determina o que chamamos de “luz visível”, que cobre matizes que vão do violeta ao vermelho. Valores abaixo do espectro visível constituem a chamada “luz ultravioleta” e acima, a “luz infravermelha”.
Na retina, temos 3 “cones” (células fotoreceptoras) que respondem a estímulos em três regiões do espectro visível:
Cone S (short), que é sensível a ondas curtas com pico em torno de 440 nm (azul).
Cone M (medium), que é sensível a ondas médias com pico em torno de 540 nm (verde).
Cone L (long), que é sensível a ondas longas com pico em torno de 580 nm (vermelho).
Os cones M e L respondem a praticamente todos os comprimentos de onda do espectro visível, enquanto o cone S é limitado a comprimentos de até 550 nm. Descrevendo-se por \((S,M,L)\) a tripleta de estímulos no em um espaço Euclidiano 3D, é possível definir o espaço de cores dos triestimular (tristimulus color space), o qual determina o espaço de cores do olho humano. Como veremos adiante, cores e espaços de cor estão intimamente ligados ao conceito de espaço vetorial, estudados na disciplina Álgebra Linear.
As figuras abaixo simulam o comportamento do espectro e dos cones. A partir daí, algumas cores monocromáticas (únicas) foram historicamente definidas, embora os comprimentos de onda de fronteira que as definem possuam variação. De acordo com o CRC Handbook of Physics (1966), as 6 bandas de ondas do espectro que atribuem nomes a cores fundamentais que conhecemos são:
Vermelho: 647 - 700;
Laranja: 585 - 647;
Amarelo: 575 - 585;
Verde: 491 - 575;
Azul: 424 - 491; e
Violeta: 400 - 424.
Curiosidade
As cores familiares citadas anteriormente são aquelas exibidas no fenômeno do arco-íris, também chamadas de cores espectrais. Spectrum é a palavra latina para “aparência”, usada por Isaac Newton no final do século XVII para caracterizar as cores produzidas pela luz visível. Essas cores são monocromáticas, no sentido de que existem por apenas um comprimento de onda único, possuem 100% de pureza e são completamente saturadas. Misturando as cores espectrais, podemos descrever qualquer cor. Os nomes das cores espectrais possuem raízes históricas anglo-saxãs e provêm de monossílabos. Uma discussão interessante sobre as cores pode ser encontrada aqui.
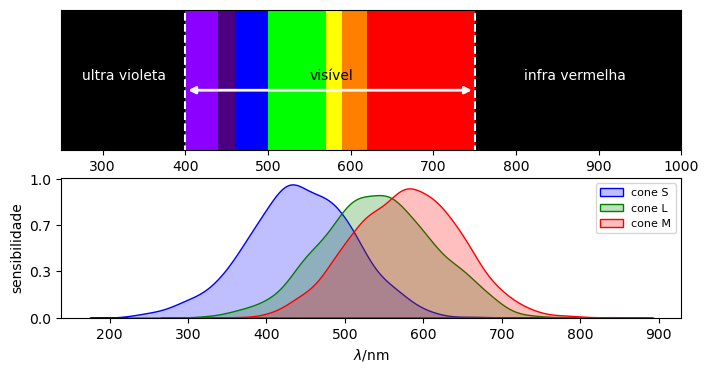
A cor da luz que emana de objetos origina-se por processos físicos. Podemos citar, por exemplo
emissão, quando o objeto é uma fonte de luz com cor determinada pelo seu espectro;
reflexão, quando algumas frequencias são refletidas pelo objeto;
transmissão, quando algumas frequencias são transmitidas através do objeto;
interferência, quando algumas frequencias são amplificadas e outras atenuadas;
6.2.2. Modelos aditivos e subtrativos#
6.2.2.1. RGB#
O modelo de cor RGB assume que uma cor é identificada por uma tripleta do tipo \(c = (r,g,b)\), em que \(r\), \(g\) e \(b\) correspondem a proporções de vermelho, verde e azul, respectivamente, que são consideradas cores primárias. Quando \(0 \leq r,g,b \leq 1\), podemos representar cada cor no modelo RGB por um vetor do espaço 3D com origem em \((0,0,0)\) e extremidade imersa no “cubo unitário” formado pelos eixos \(r\), \(g\) e \(b\).
Geometricamente, a cor preta seria então representada justamente pelo vetor \(\vec{o} = (r=0,g=0,b=0)\), o que remete à ausência de luz, em certo sentido, razão pela qual preto não é considerada uma cor propriamente dita. Analogamente aos vetores canônicos \(\vec{i}\), \(\vec{j}\) e \(\vec{k}\) do espaço 3D, os vetores \((1,0,0)\), \((0,1,0)\) e \((0,0,1)\) formariam uma base para que, a partir de tonalidades das cores vermelho, verde e azul. A partir disso, é imeditado reconhecer que, segundo o modelo RGB, qualquer cor é dada por uma combinação linear de tonalidades de \(r\), \(g\) e \(b\), ou seja:
Nestes termos, o vetor \(\vec{c_0} = (0,0,0)\) seria a cor “preto”, o vetor \(\vec{c_1} = (1,1,1)\) seria “branco”, a família de vetores \(\vec{c_g} = k\vec{c_0}, \ \ 0 < k < 1\), determinaria os “tons de cinza”, e qualquer outra combinação, as demais cores. Entretanto, vale ressaltar que o olho humano é limitado. Ele consegue distinguir cerca de 7 - 10 milhões de cores. Embora seja uma quantidade extremamente grande, isso impõe, de certa forma, finitude sobre os valores de \(r\), \(g\) e \(b\).
Nos sistemas digitais modernos, os valores de \(r\), \(g\) e \(b\) limitam-se aos números inteiros positivos entre 0 e 255, inclusive. Isto é, em termos de “voxels” discretos (“pixels volumétricos”), o nosso “cubo unitário” de cores infinitas seria reduzido a uma espécie de cubo mágico capaz de identificar, no máximo 256 x 256 x 256 = 16.777.216 cores (aproximadamente 16 milhões!). A Fig. 6.1 (veja aqui), traz uma representação geométrica do cubo RGB.
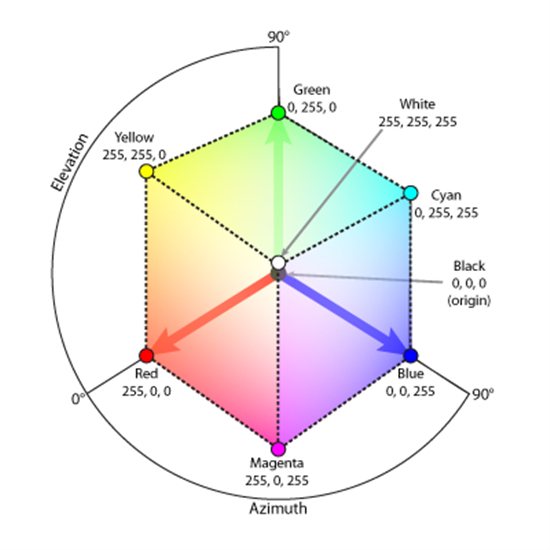
Fig. 6.1 Cubo de cores RGB: representação geométrica do espectro de cores possíveis para valores 0 - 255.#
Curiosidade
As mais de 16 milhões de cores RGB que vemos em qualquer tela True Color moderna equivalem a ter imagens processadas com 8 bits por canal, i.e. \((2^8)^3\) cores. Veja uma discussão interessante entre bits e cores neste post.
RGB é um modelo aditivo (Fig. 6.2), significando que a cor percebida pode ser representada pela soma de valores numéricos de suas componentes, como já fizemos acima. Neste modelo, vermelho, verde e azul são chamadas cores primárias. Como a cor preta equivale a um “elemento neutro”, pelo modelo aditivo, podemos escrever, algebricamente,
preto + vermelho = vermelho
preto + verde = verde
preto + azul = azul.
Entretanto,
vermelho + verde = amarelo
verde + azul = ciano
azul + vermelho = magenta
vermelho + verde + azul = branco
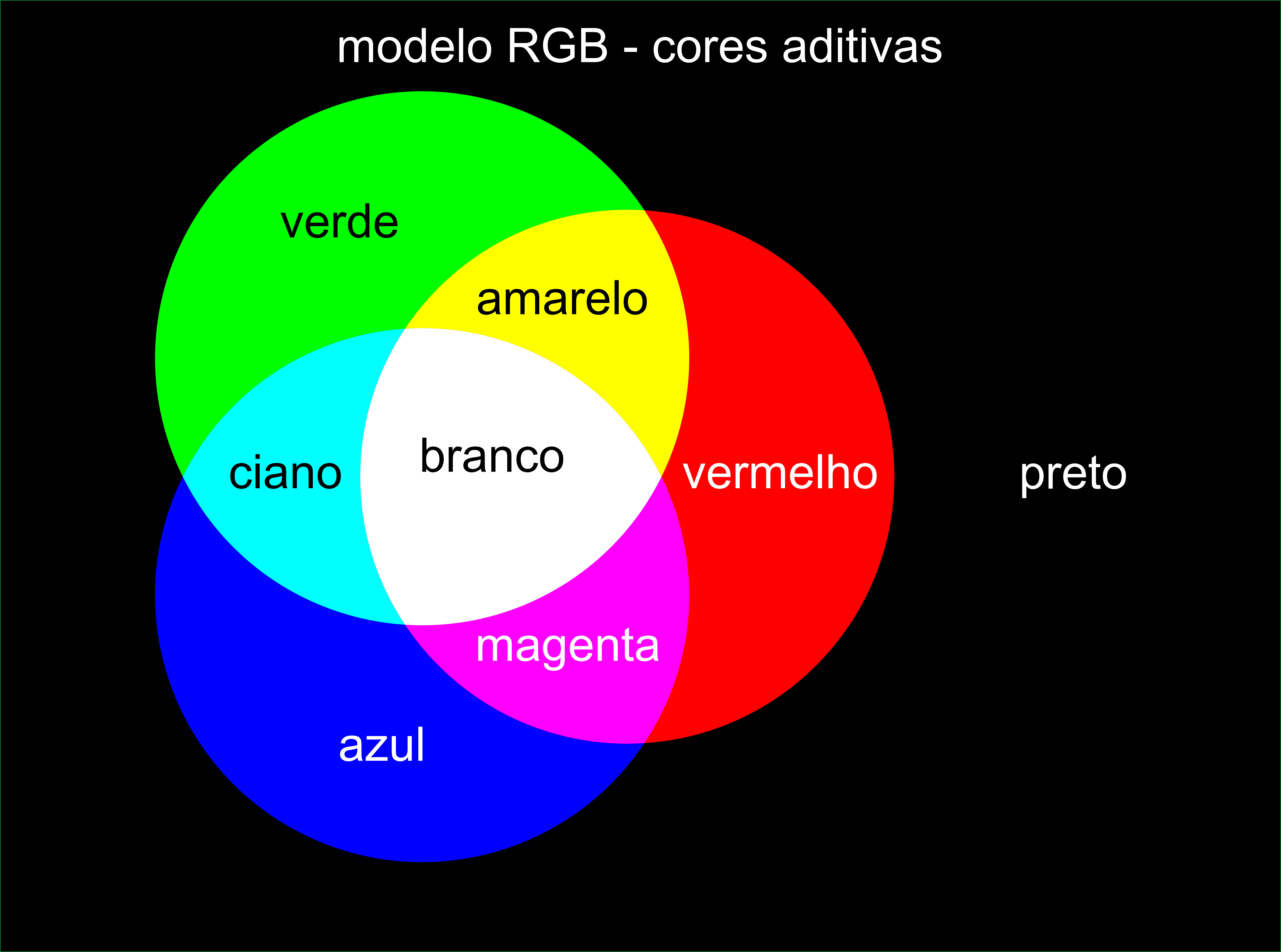
Fig. 6.2 Modelo fundamental de mistura aditiva de cores RGB.#
6.2.2.2. CMYK#
Diferentemente do modelo RGB, o modelo de cor CMYK assume que uma cor é identificada por uma quadripleta do tipo \(c = (c,m,y,k)\), em que \(c\), \(m\), \(y\), e \(k\) correspondem a proporções de ciano, magenta, amarelo e preto, respectivamente. As três primeiras são consideradas cores subtrativas primárias e preto uma quarta componente que gera tonalidades escuras. Por isso, este modelo também é conhecido como CMY.
As cores subtrativas (Fig. 6.3) agem em complementaridade às aditivas primárias e servem como filtros que as absorvem. Assim, ciano, magenta e amarelo são cores complementares a vermelho, verde e azul, nesta ordem. O modelo CMYK é preferível para impressão porque o espectro de cores CMYK é significativamente menor e composto por pigmentos, ao passo que RGB é preferível para telas e dispositivos eletrônicos por ser composto por luz.
A ausência de pigmentos é o papel branco. Isto significa que o papel permanece “branco” quando iluminado pela luz branca. Adicionar pigmentos a ele é como subtrair certos comprimentos de onda. Então, algebricamente:
branco - vermelho = ciano
branco - verde = magenta
branco - azul = amarelo.
Porém,
vermelho + ciano = branco
verde + magenta = branco
azul + amarelo = branco
e
ciano + magenta = azul
magenta + amarelo = vermelho
amarelo + ciano = verde
ciano + magenta + amarelo = preto
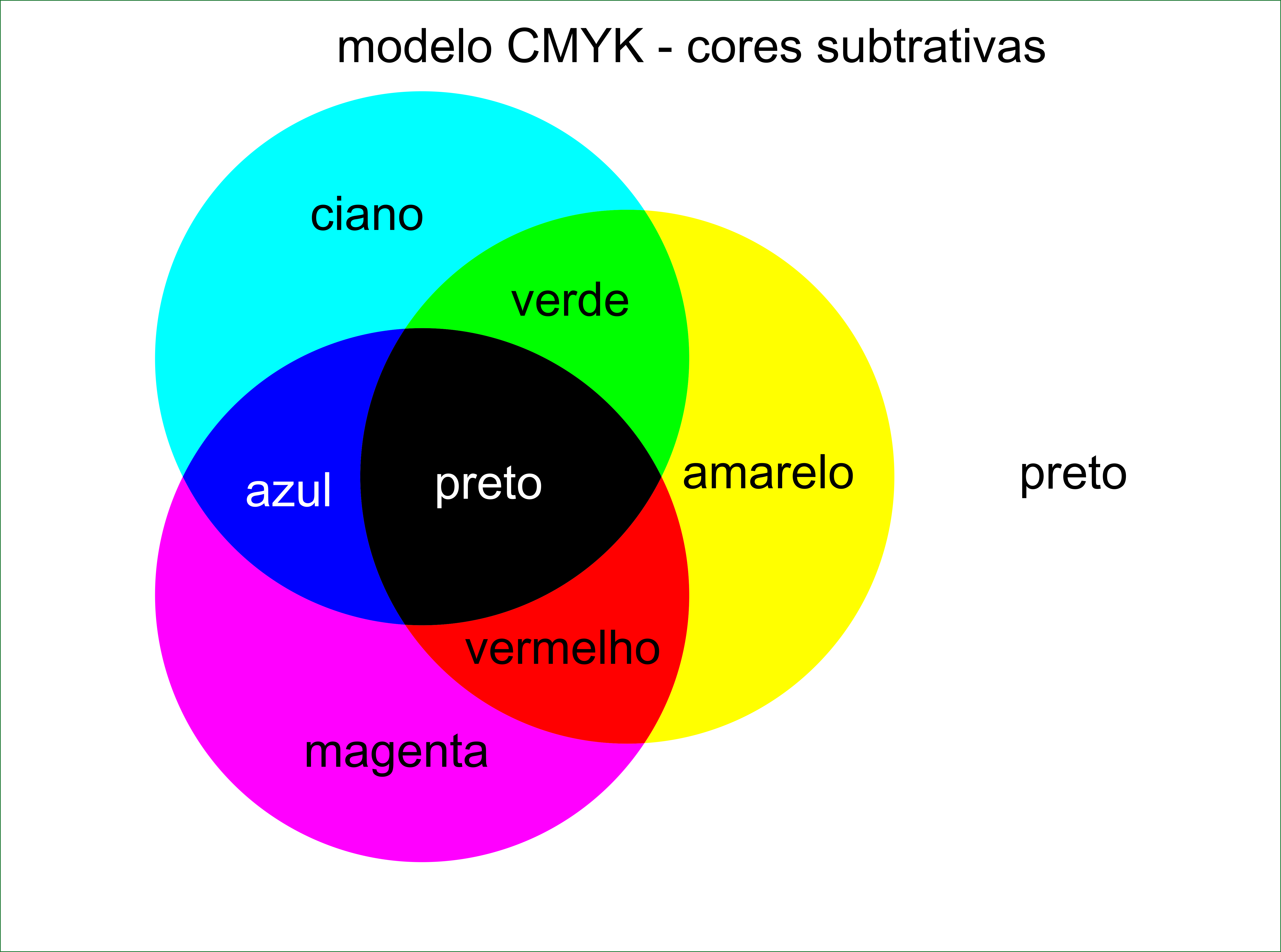
Fig. 6.3 Modelo fundamental de mistura subtrativa de cores CMY/K.#
6.2.3. Modelos geométricos#
Outros diversos modelos de cor tridimensionais em formatos cônicos, cilíndricos ou esféricos foram desenvolvidos ao longo do tempo, tais como HSL, HSV, HSI, HCL, HSB, NCS, XYZ, entre outros. A Fig. 6.4 (disponível aqui) exibe os modelos HSL e HSV em formas geométricas diferentes. Desses, o HSL (Hue, Saturation, Luminosity) é considerado um dos mais acessíveis para aplicação em visualização de dados. Ele é uma representação cilíndrica do modelo RGB. Portanto, nós o consideraremos para estudo.

Fig. 6.4 Modelos HSL e HSV com variadas representações geométricas.#
6.2.3.1. HSL#
O modelo HSL também é tridimensional. Suas componentes são:
Hue (matiz), que varia na direção azimutal do cilindro e define a cor “verdadeira”. Para o modelo CIECAM02 de colorimetria, o matiz é tecnicamente definido como “o grau com que um estímulo pode ser descrito como semelhante ou diferente de estímulos descritos como vermelho, laranja, amarelo, verde, azul ou violeta”. No sistema cilíndrico de coordenadas, a cor vermelha primária (matiz puro) está na coordenada 0 grau, a cor verde primária em 120 graus e a azul em 240 graus. O matiz é um atributo qualitativo da cor porque é definido por diferença e não por escala. Não existem tints, shades ou tints (vide Seção 6.2.5).
Saturation (saturação), que varia na direção radial do cilindro e define a pureza do matiz. A cor plenamente saturada é vívida (vivid). À medida que a insaturamos até o estado de tons de cinza, ou acromaticidade, ou neutralidade (eixo central do cilindro), a cor torna-se muda (muted). Portanto, um matiz com 0% de saturação neutro (mudo), ao passo que um matiz com 100% de saturação é puro (vívido). A saturação é um parâmetro quantitativo da cor.
Luminosity (luminosidade), que define a direção axial do cilindro e define o contraste do matiz. A luminosidade, tecnicamente, não é sinônimo de brilho, mas ela pode ser entendida como um controlador entre tons claros e escuros. Assim como a saturação, a luminosidade também é um parâmetro quantitativo da cor.
Abaixo, utilizamos as funções seaborn.palplot() e seaborn.hls_palette para demonstrar variações dos valores das componentes \(h\), \(s\), e \(l\) no modelo de HSL, no qual a cor é uma tripleta em coordenadas cilíndricas dada por \(c=(h,s,l)\).
Variação de matizes com 100% de saturação e luminosidade média.
from seaborn import palplot, hls_palette
# cores puras do arco-íris
palplot(hls_palette(n_colors=5, h=0, s=1, l=0.5))
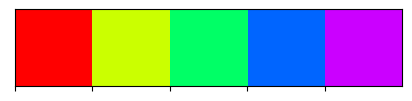
# matiz 33%
palplot(hls_palette(n_colors=5, h=0.5, s=1, l=0.5))
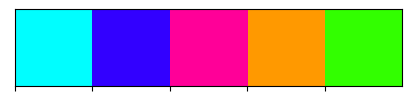
# matiz 66%
palplot(hls_palette(n_colors=5, h=0.1, s=1, l=0.5))
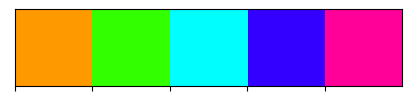
Matiz 100% com variação de saturação e luminosidade média.
# saturação 80%
palplot(hls_palette(n_colors=5, h=1, s=.75, l=0.5))
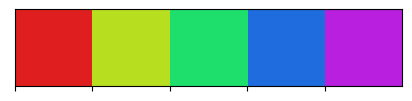
# saturação 50%
palplot(hls_palette(n_colors=5, h=1, s=.5, l=0.5))
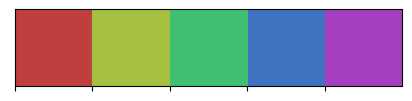
# saturação 10%
palplot(hls_palette(n_colors=5, h=1, s=.1, l=0.5))
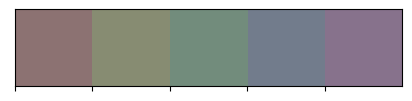
Matiz e saturação 100% e luminosidade variável.
# luminosidade 90%
palplot(hls_palette(n_colors=5, h=1, s=1, l=.9))
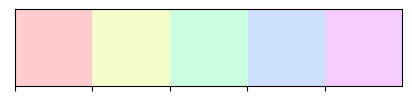
# luminosidade 40%
palplot(hls_palette(n_colors=5, h=1, s=1, l=.4))
# luminosidade 10%
palplot(hls_palette(n_colors=5, h=1, s=1, l=.1))

6.2.4. Cores em código HEX#
A representação de cores por código hexadecimal (hex codes) emergiu como um sistema prático para trabalhar com desenvolvimento web. Entretanto, passou a ser utilizado para diversos fins em visualização de dados devido à sua simplicidade de uso e facilidade de compreensão. Uma tripleta HEX é um número de 6 dígitos (3 bytes) hexadecimais do tipo AABB00 bastante utilizada em linguagens HTML e CSS para estilizar páginas da internet e também em artes gráficas. Em geral, usa-se uma tralha (#) antes do código por razões sintáticas.
O código HEX nada mais é do que uma representação implícita do modelo RGB. Os dígitos 1 e 2 (byte 1) controlam a proporção de vermelho, 3 e 4 a proporção de verde (byte 2), e 5 e 6 a proporção de azul (byte 3). Como o sistema hexadecimal admite os dígitos de 0 a 9 e as letras de A a F (equivalentes aos dígitos de 10 a 15), existem exatamente 16 possibilidades por dígito de hex code, ou seja até \(16^6 = 16.777.216\) cores representáveis.
Para se converter valores RGB em HEX, devemos adotar as coordenadas discretas de 0 a 255 ou converter a escala 0 - 1 para 0 - 255 multiplicando o número por 255 e, então realizar a divisão inteira por 16. O quociente da divisão equivale ao primeiro dígito, o resto ao segundo. Fazendo o mesmo para cada coordenada, obteremos o hex code correspondente.
6.2.4.1. Exemplo de conversão RGB > HEX#
Para a cor RGB(1,0.5,0.3):
multiplicamos por 255 para ter RGB(255,127,76). Obs.: se a tupla já for inteira, este passo é ignorado.
realizamos a divisão inteira por componente para obter a tupla de quocientes (15,7,4);
tomamos o resto da divisão inteira por componente para obter a tupla de restos (15,15,12);
convertemos os dígitos maiores do que 9 para letras nas tuplas para obter (F,7,4) e (F,F,C);
juntamos as tuplas elemento a elemento para formar os bytes chegando ao hex code FF7F4C
Abaixo, plotamos dois retângulos especificando as cores por tupla RGB e código HEX para compararmos o resultado.
from matplotlib.pyplot import subplots
from matplotlib.patches import Rectangle
fig, ax = subplots(1,2,figsize=(8,1),constrained_layout=True)
# tupla de cor (r,g,b,a), com a = opacidade
ax[0].add_patch(Rectangle(xy=(0,0),width=1, height=1, color=(1,0.5,0.3,1.0)))
ax[0].text(0.35,0.5,'RGB(255,127,76)',fontdict={'color':'k'})
ax[0].set_axis_off()
# cor com hex code
ax[1].add_patch(Rectangle(xy=(0,0),width=1, height=1, color='#FF7F4C'))
ax[1].text(0.4,0.5,'#FF7F4C',fontdict={'color':'k'})
ax[1].set_axis_off()

Uma função para converter tuplas RGB em código HEX poderia ser codificada conforme abaixo. Você pode aperfeiçoá-la para tratar a exceção do caso em que o usuário entra com valores numéricos válidos, porém misturados entre tipos int e float, ou modificar os argumentos de entrada para a forma (r: int, g: int, b: int).
def rgb2hex(rgb : tuple):
'''Conversor simples de cor RGB para HEX code'''
from numpy import asarray, array
rgb = asarray(rgb)
# checking
if all((rgb >= 0) & (rgb <= 1)):
rgb = array(rgb*255,dtype=int)
elif all((rgb/255 >= 0) & (rgb/255 <= 1)): #TODO caso (int,float,float)
pass
else:
raise ValueError('Tupla RGB deve conter valores entre [0,1] ou [0,255].')
# conversão
q = rgb // 16
q = [hex(qi).removeprefix('0x') for qi in q]
r = rgb % 16
r = [hex(ri).removeprefix('0x') for ri in r]
# string
hex_ = '#'
for i in range(3):
hex_ += q[i] + r[i]
return hex_
Pelos testes abaixo, conseguimos verificar que a função se comporta como esperaríamos tanto para tuplas de valores fracionados quanto para tuplas de valores inteiros (0 - 255).
# teste 1
rgb = (1,0.5,0.3)
rgb2hex(rgb)
'#ff7f4c'
# teste 2
rgb = (255,127,76)
rgb2hex(rgb)
'#ff7f4c'
6.2.4.2. Exemplos de cores CSS#
A seguir plotamos um mosaico das cores CSS predefinidas do matplotlib e seus hex codes.
from matplotlib.colors import CSS4_COLORS
from matplotlib.pyplot import subplots
from matplotlib.patches import Rectangle
fig, ax = subplots(37,4,figsize=(10,8),constrained_layout=True)
fig.suptitle('Cores CSS predefinidas do matplotlib e seus hex codes',fontsize=8)
# cores CSS
css = CSS4_COLORS
ck,cv = list(css.keys()),list(css.values())
# mosaico de cores: len(css)/4 = 37 x 4
for k in range(1,5):
nms = ck[(k-1)*37:k*37]
cols = cv[(k-1)*37:k*37]
for a in range(37):
ax[a,k-1].add_patch(Rectangle(xy=(0,0),width=0.1, height=1, color=cols[a]))
s = f'\'{nms[a]}\': {cols[a]}'
ax[a,k-1].text(0.15,0.5,s,fontdict={'color':'k','fontsize':8,'va':'center'})
ax[a,k-1].set_axis_off()

6.2.5. Misturas de cor#
Alguns termos utilizados para fazer referência a misturas de cor decorrentes de cores puras (cores que não podem ser obtidas a partir de outras) são empregados pelos teóricos da cor. Esses termos não possuem tradução imediata para o português, mas podem ser especificados com auxílio de prefixo “tons de”. São eles:
Tints (tons de branco): são cores que, misturadas com branco, produzem variações de luminosidade;
Shades (tons de preto): são cores que, misturadas com preto, produzem variações de escuridão;
Tones (tons): são cores misturadas com cinza, preto ou branco.
O diagrama da Fig. 6.5 descreve a relação entre esses termos.
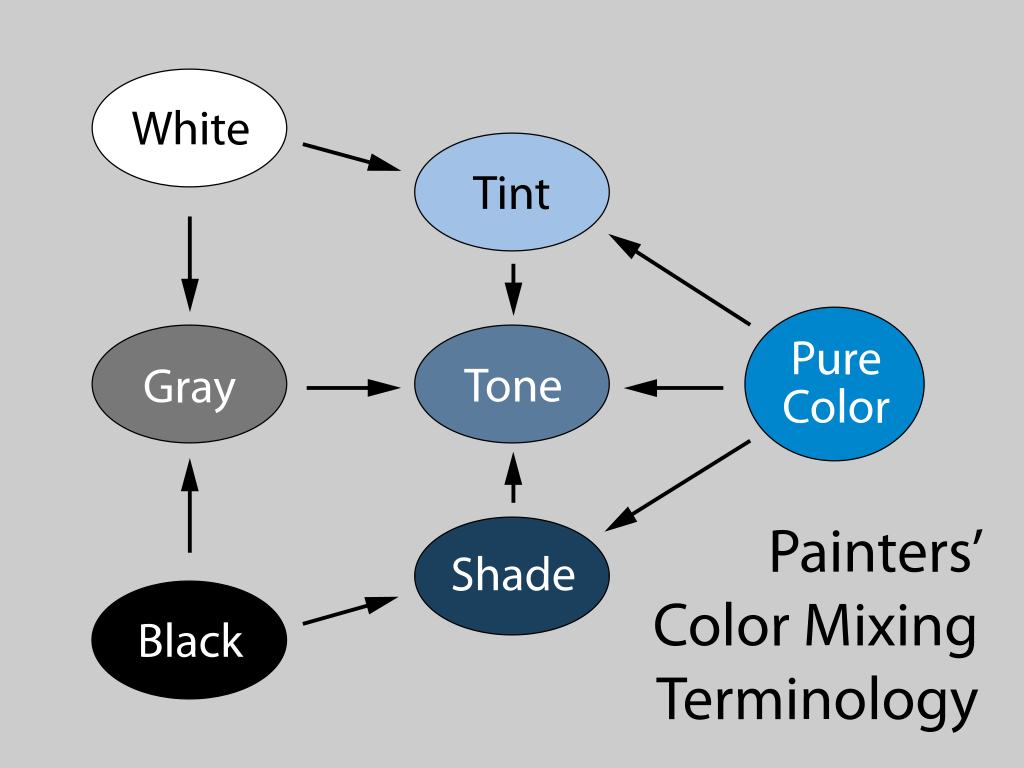
Fig. 6.5 Diagrama de termos relativos a tonalidades de cor.#
6.3. Outros esquemas de cor#
As escalas de cor que estudamos na Seção 6.1 às vezes são chamadas de esquemas de cor. Existem diversos esquemas com aplicações e usos específicos (p.ex. triádico, tetrádico, análogo) que não exploraremos com detalhes neste capítulo.Porém, vale ressaltar ainda alguns deles, que também sugerem terminologias úteis:
Esquema monocromático: composto por cores derivadas de um único matiz adicionadas de branco, cinza ou preto, isto é, seus tints, tones e shades.
Esquema complementar: composto pelas cores que cancelam os matizes de outras, segundo o princípio subtrativo.
Esquema acromático: composto por cores insaturadas, acromáticas, ou aproximadamente neutras. Cores acromáticas puras incluem preto, branco, cinzas e beges. Cores aproximadamente neutras incluem marrons, tons canelados, pastéis e escurecidos. Cores neutras podem ser produzidas pela mistura de cores puras com preto, branco, cinza, ou com duas cores complementares.
Outros termos úteis neste contexto são relacionados a paletas de cores, a exemplo de color swatch e color wheel.
6.3.1. Esquemas de propriedade comercial#
No cenário internacional, muitas empresas disputam o “mercado da cor” e das artes gráficas. Algumas delas possuem sistemas de classificação de cor próprios e patenteados. Uma parte delas é bastante conhecida no Brasil, outra nem tanto. Para efeito de expansão de conhecimento, seguem abaixo links para algumas marcas devotadas às cores:
Faber-Castell© (veja tabela de cores aqui
Uma tabela de conversão de cores entre alguns dos sistemas acima pode ser encontrada nesta página.
6.4. Teoria dos espaços de cor#
6.4.1. Espaços de cor CIE#
Modelos de cor e espaços de cor às vezes são terminologias que se confundem, embora existam propriedades intrínsecas a serem destacadas para que um espaço de cor seja realmente definido. Um espaço de cor, compreendido de maneira direta, é uma estrutura de organização de cores. Porém, esta resposta pode ser pouco esclarecedora, levando-nos a adentrar um pouco mais no conhecimento teórico.
O que separa um modelo de cor, como o RGB, por exemplo, de um espaço de cor, como o CIELAB, é uma espécie de função de mapeamento de cor que está vinculada à percepção real do olho humano das cores. Em 1931, a International Commission on Illumination (em francês, Commission Internationale de l’Éclairage - CIE), a autoridade internacional em matéria de padrões para luz e cor, estabeleceu o observador padrão (colorimétrico) como a função de mapeamento. Uma vez que os cones triestimulares S, M, L (veja a Seção 6.1) dependem do campo de visão do observador, o observador padrão é uma ponderação das respostas aos estímulos da visão considerando parâmetros experimentais e a ciência da colorimetria, que forma a base para descrever uma cor como três numeros.
No princípio, o experimento do observador padrão tratou as componentes de cromaticidade formadoras da cor como \(L^{*}\), \(a^{*}\) e \(b^{*}\), representando nesta ordem, a luminosidade, a resposta a estímulos de verde/vermelho e a resposta a estímulos de azul-amarelo. Da junção de CIE com as iniciais utilizadas decorre o nome CIELAB, ou espaço CIE 1931, que é um espaço de cor independente de dispositivo. Na prática, monitores, telas e dispositivos eletrônicos para visualização de imagens coloridas representam as cores de maneira diferente, razão pela qual a necessidade por um padrão emergiu.
Relacionados ao espaço CIELAB, estão os espaços CIEXYZ e CIERGB. No espaço CIEXYZ, \(Z\) é a componente da luminosidade, \(Z\) é a componente “quase-azul” (equivalente a azul no CIERGB) e \(X\) é a componente das misturas das cores RGB.
6.4.2. Espectro e componentes#
A energia física (radiância) é expressa em um espectro de 31 componentes representando bandas de 10 nanômetros, o que leva à faixa do espectro visível de aproximadamente 400 - 700 nm. Isto significa que, a rigor, uma cor seria representada por 31 componentes. Uma vez que isso é irrazoável, a ponderação dessas componentes no espectro permite que reduzamos sua complexidade a apenas 3 componentes.
As 3 componentes geralmente utilizadas dependerão, por sua vez, do espectro de energia. Nos experimentos primários da CIE, as funções de mapeamento – também chamadas de color matching functions (CMFs) – para o observador padrão foram definidas como superposições de curvas gaussianas dadas pela expressão
onde \(\lambda \, [nm]\) é o comprimento de onda, \(\mu\) o valor médio da distribuição, \(\sigma_1\) o desvio à esquerda da média e \(\sigma_2\) o desvio à direita da média.
Por sua vez, as CMFs para as respostas triestimulares XYZ para o espaço CIEXYZ, foram dadas pelas ponderações a seguir:
A partir daí, definindo-se o espectro de energia por uma função \(p(\lambda)\), uma cor é definida pelo vetor
para o espectro compreendido entre comprimentos de onda no intervalo \([\lambda_{min},\lambda_{max}]\).
6.4.3. Relacionamento com a Álgebra Linear#
Tendo em vista que a interpretação triestimular dependerá do espaço de cor considerado, haja vista os parâmetros que o definem, uma cor, genericamente, é função de um espectro de distribuição da luz, \(p(\lambda)\), e da sensibilidade dos 3 cones de percepção visual. Escrevendo a função de sensibilidade do i-ésimo cone como \(s_i(\lambda)\) para um espaço de cor \(E\), podemos expressar as componentes de uma cor \(c\) em \(E\) como
Notemos, porém, que o vetor \(\vec{c}\) do qual \(c_i\) são suas componentes, é, na verdade, um vetor que possui integrais definidas com integrandos “contínuos”. Na prática, as cores são representadas por pixels e canais de cor discretos, sendo necessário trabalhar com arrays de dimensão até 3, o que nos remete a operações matriz-vetor.
Assim, em termos de matemática discreta, a cor, grosso modo, é representada por uma operação algébrica do tipo
com \(\mathbf{c} \in \mathbb{R}^3\), \(\mathbf{S} \in \mathbb{R}^{n \times 3}\) e \(\mathbf{p} \in \mathbb{R}^n\).
De igual modo, a conversão entre espaços de cor dá-se por meio de operações matriciais, porque, no final das contas, cada cor é identificada como um vetor \(c\) de 3 coordenadas identificado com uma posição de um subespaço vetorial tridimensional \(\mathcal{E}\). Por exemplo, para converter cores do sistema RGB para XYZ, devemos resolver uma equação matricial do tipo:
onde \([X \, Y \, Z]^T\) é o vetor de coordenadas da cor no sistema XYZ, \([R \, G \, B]^T\) o vetor equivalente no sistema RGB e \(\mathbf{M}\) a matriz de transformação. A conversão no sentido inverso depende da inversa de \(\mathbf{M}\). Entretanto, como existem diversos espaços RGB, as matrizes \(\mathbf{M}\) e \(\mathbf{M}^{-1}\) também diferirão caso a caso.
A seguir, mostramos os pares de matrizes para conversão RGB-XYZ para dois espaços RGB comuns considerando a referência de cor branca \(D_{65}\) (chamada de reference white):
Adobe RGB (1998)
Apple RGB
6.5. Referências#
- Kir16
Andy Kirk. Data visualisation: A handbook for data driven design. Sage, 2016.

