14. Python Numérico (numpy): arrays¶

14.1. Introdução ao Numpy¶

O pacote NumPy (lido como NUMerical PYthon) dá acesso a

uma nova estrutura de dados chamada array que permite
operações vetoriais e matriciais eficientes. Ela também fornece
uma série de operações de álgebra linear (como a resolução de sistemas de equações lineares e a computação de autovetores/autovalores).

14.1.1. Histórico¶

Alguns conhecimentos prévios: existem duas outras implementações que fornecem quase a mesma funcionalidade do NumPy: Numeric e numarray.

Numeric foi a primeira provisão de um conjunto de métodos numéricos (semelhante ao Matlab) para Python. Ela evoluiu a partir de um projeto de doutorado.
Numarray é uma implementação de Numeric com certas melhorias (mas, para nossos propósitos, Numeric e numarray comportam-se praticamente de modo idêntico).
No início de 2006, decidiram combinar os melhores aspectos do Numeric e numarray no Scipy e fornecer o array (“esperançosamente”, um produto final) como um tipo de dado incluído no módulo “NumPy”.

No restante do material, usaremos o pacote “NumPy” como fornecido pelo (novo) SciPy. Se, por algum motivo, isso não funcionar para você, é porque, provavelmente, sua versão do SciPy seja muito antiga. Nesse caso, Numeric ou numarray podem estar instaladas e devem fornecer quase que as mesmas capacidades. [5]

14.1.2. Arrays¶

Apresentamos um novo tipo de dado (fornecido pelo NumPy) que é chamado de array. Uma matriz é “parecida” com uma lista, mas um array pode guardar apenas elementos do mesmo tipo (ao passo que uma lista pode misturar diferentes tipos de objetos). Isto significa que arrays são mais eficientes em armazenamento (porque não precisamos armazenar um tipo para cada elemento). Arrays também são a estrutura de dados de escolha para cálculos numéricos quando lidamos com vetores e matrizes. Vetores e matrizes (e matrizes com mais de dois índices) são todos chamados de arrays pela biblioteca NumPy.

14.1.2.1. Vetores (Arrays 1D)¶

A estrutura de dados de que precisaremos mais frequentemente é um vetor. Aqui estão alguns exemplos de como podemos gerar um:

Conversão de uma lista (ou tupla) em uma matriz usando numpy.array:

import numpy as N
x = N.array([0, 0.5, 1, 1.5])
print(x)

[ 0.   0.5  1.   1.5]

Criação de um vetor usando “ARRAYRange”:

x = N.arange(0, 2, 0.5)
print(x)

[ 0.   0.5  1.   1.5]

Criação de vetor de zeros

x = N.zeros(4)
print(x)

[ 0.  0.  0.  0.]

Uma vez que a matriz for estabelecida, podemos definir e recuperar valores individuais. Por exemplo:

x = N.zeros(4)
x[0] = 3.4
x[2] = 4
print(x)
print(x[0])
print(x[0:-1])

[ 3.4  0.   4.   0. ]
3.4
[ 3.4  0.   4. ]

Observe que, tendo o vetor, podemos executar cálculos em cada elemento no vetor com uma única declaração:

x = N.arange(0, 2, 0.5)
print(x)
print(x + 10)
print(x ** 2)
print(N.sin(x))

[ 0.   0.5  1.   1.5]
[ 10.   10.5  11.   11.5]
[ 0.    0.25  1.    2.25]
[ 0.          0.47942554  0.84147098  0.99749499]

14.1.2.2. Matrizes (Arrays 2D)¶

Aqui estão duas maneiras de criar um array bidimensional:

Ao converter uma lista de listas (ou tuplas) em uma matriz:

x = N.array([[1, 2, 3], [4, 5, 6]])
x

array([[1, 2, 3],
       [4, 5, 6]])

Usando o método zeros para criar uma matriz com 5 linhas e 4 colunas

x = N.zeros((5, 4))
x

array([[ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.]])

O “formato” de uma matriz pode ser consultado assim (aqui temos 2 linhas e 3 colunas):

x=N.array([[1, 2, 3], [4, 5, 6]])
print(x)
x.shape

[[1 2 3]
 [4 5 6]]

(2, 3)

Elementos individuais podem ser acessados e configurados usando esta sintaxe:

x=N.array([[1, 2, 3], [4, 5, 6]])
x[0, 0] 

x[0, 1]

x[0, 2]

x[1, 0]

x[:, 0]

array([1, 4])

x[0,:]

array([1, 2, 3])

14.1.3. Conversão de array para lista ou tupla¶

Para converter um array de volta para uma lista ou tupla, podemos usar as funções padrão list(s) e tuple(s) do Python, que levam uma sequência s como argumento de entrada e retornam uma lista e uma tupla, respectivamente:

a = N.array([1, 4, 10])
a

array([ 1,  4, 10])

list(a)

[1, 4, 10]

tuple(a)

(1, 4, 10)

14.1.4. Operações de Álgebra Linear padrão¶

14.1.4.1. Multiplicação de matrizes¶

Dois arrays podem ser multiplicados na forma usual da álgebra linear usando numpy.matrixmultiply. Aqui está um exemplo:

import numpy as N
import numpy.random       
A = numpy.random.rand(5, 5)    # gera uma matriz aleatória 5x5
x = numpy.random.rand(5)       # gera um vetor de 5 elementos
b=N.dot(A, x)                  # multiplica a matriz A pelo vetor x 

14.1.4.2. Solução de sistemas de equações lineares¶

Para resolver um sistema de equações Ax = b que é dado na forma matricial (i.e. A é uma matriz e x e b são vetores, onde A e b são conhecidos e queremos encontrar o vetor desconhecido x), podemos usar o pacote de álgebra linear (linalg) do numpy:

import numpy.linalg as LA
x = LA.solve(A, b)

14.1.4.3. Calculando Autovetores e Autovalores¶

Aqui está um pequeno exemplo que calcula os autovetores e autovalores [triviais] (eig) da matriz identidade (eye)):

import numpy
import numpy.linalg as LA
A = numpy.eye(3)     #'eye'->I->1 (matriz identidade)
print(A)

[[ 1.  0.  0.]
 [ 0.  1.  0.]
 [ 0.  0.  1.]]

auto_valores, auto_vetores = LA.eig(A)
print(auto_valores)

[ 1.  1.  1.]

print(auto_vetores)

[[ 1.  0.  0.]
 [ 0.  1.  0.]
 [ 0.  0.  1.]]

Observe que cada um desses comandos fornece sua própria documentação. Por exemplo, help(LA.eig) irá lhe dizer tudo sobre a função de autovetor e autovalor (uma vez que você tenha importado numpy.linalg como LA).

14.1.4.4. Ajuste polinomial de curvas¶

Vamos supor que temos dados x-y para os quais queremos ajustar um polinômio (no sentido de quadrados mínimos).

O NumPy fornece a rotina polyfit(x, y, n) (que é semelhante à função polyfit do Matlab, que toma por argumentos uma lista x</ span> de valores x para os pontos dos dados, uma lista y de valores y para os mesmos pontos de dados e n</ span>, a ordem desejada do polinômio que será determinado para ajustar os dados.

%matplotlib inline
import numpy

# demonstração - ajuste de curva: `xdata` e `ydata` são dados de entrada
xdata = numpy.array([0.0 , 1.0 , 2.0 , 3.0 , 4.0 , 5.0])
ydata = numpy.array([0.0 , 0.8 , 0.9 , 0.1 , -0.8 , -1.0])

# ajuste por um polinômio cúbico (ordem = 3) 
z = numpy.polyfit(xdata, ydata, 3)

# z é um array de coeficientes, maior grau primeiro, i . e .
#                 X^3            X^2          X             0
# z = array ([ 0.08703704 , -0.81349206 , 1.69312169 , -0.03968254])

# É conveniente usar objetos ‘poly1d‘ para lidar com polinômios:
p = numpy.poly1d(z) # cria uma função polinomial p a partir dos coeficientes
                    # e p pode ser avaliado para todo x então.

# cria plot
xs = [0.1 * i for i in range (50)]
ys = [p(x) for x in xs]   # avalia p(x) para todo `x` na lista `xs`

import pylab
pylab.plot(xdata, ydata, 'o', label='dados')
pylab.plot(xs, ys, label='curva ajustada')
pylab.ylabel('y')
pylab.xlabel('x')

<matplotlib.text.Text at 0x10b7098d0>

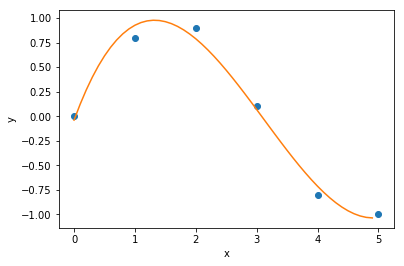
_images/14-python-numerico-numpy_37_1.png

A figura mostra a curva ajustada (linha contínua) juntamente com os pontos de dados calculados precisos.

14.1.5. Mais exemplos NumPy¶

Podem ser encontrados aqui: http://www.scipy.org/Numpy_Example_List

14.1.6. NumPy para usuários do Matlab¶

Há uma página dedicada que explica o módulo NumPy a partir da perspectiva de um usuário (experiente) do Matlab em http://docs.scipy.org/doc/numpy-dev/user/numpy-for-matlab-users.html.

Introdução à Linguagem Python para Ciências Computacionais e Engenharia