12. Computação simbólica¶
12.1. SymPy¶
Nesta seção, apresentamos algumas funcionalidades básicas da biblioteca SymPy (SYMbolic Python). Em contraste com a computação numérica (envolvendo números), no cálculo simbólico estamos processando e transformando variáveis genéricas.
A página inicial do SymPy (http://sympy.org/) fornece a documentação completa (e atualizada) para esta biblioteca.
A computação simbólica é muito lento em comparação com as operações em ponto flutuante e, assim, geralmente não muito adequada para simulação direta. No entanto, é uma ferramenta poderosa no suporte à preparação do código e trabalho simbólico. Ocasionalmente, usamos operações simbólicas em simulações para elaborar o código numérico mais eficiente, antes que seja executado.
12.1.1. Saída¶
Antes de começarmos a usar o SymPy, chamaremos init_printing. Isto diz ao SymPy para mostrar as expressões em um formato mais conveniente.
import sympy
sympy.init_printing()
12.1.2. Símbolos¶
Antes de começarmos a executar qualquer operação simbólica, precisamos criar variáveis simbólicas usando a função Symbol do SymPy:
from sympy import Symbol
x = Symbol('x')
type(x)
sympy.core.symbol.Symbol
y = Symbol('y')
2 * x - x
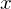
x + y + x + 10*y
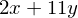
y + x - y + 10
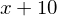
Podemos abreviar a criação de múltiplas variáveis simbólicas usando a função symbols. Por exemplo, para criar as variáveis simbólicas x, y e z, podemos usar
import sympy
x, y, z = sympy.symbols('x,y,z')
x + 2*y + 3*z - x
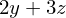
Uma vez que terminarmos a manipulação dos termos, às vezes desejamos inserir números para as variáveis. Isso pode ser feito usando o método subs.
from sympy import symbols
x, y = symbols('x,y')
x + 2*y
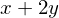
x + 2*y.subs(x, 10)
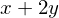
(x + 2*y).subs(x, 10).subs(y, 3)
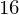
(x + 2*y).subs({x:10, y:3})
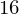
Também podemos substituir uma variável simbólica por outra, como neste exemplo, em que y é substituído por x antes de substituirmos x pelo número 2.
termo = 3*x + y**2
termo
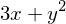
termo.subs(x, y)
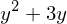
termo.subs(x, y).subs(y, 2)
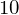
A partir deste ponto, alguns fragmentos de código e exemplos que apresentamos assumirão que os símbolos necessários já foram definidos. Se você tentar um exemplo e o SymPy der uma mensagem como NameError: name 'x' is not defined, é porque você precisa definir o símbolo usando um dos métodos acima.
12.1.3. isympy¶
O executável isympy é um wrapper em torno do ipython que cria as variáveis simbólicas (reais) x, y e z, as variáveis inteiras simbólicas k, m e n, e as variáveis de função simbólica f, g e h, e importa todos os objetos do SymPy.
Isto é conveniente para descobrir novos recursos ou fazer experimentos de forma interativa
$> isympy Python 2.6.5 console for SymPy 0.6.7
These commands were executed:
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z = symbols('xyz')
>>> k, m, n = symbols('kmn', integer=True)
>>> f, g, h = map(Function, 'fgh')
Documentation can be found at http://sympy.org/
In [1]:
12.1.4. Tipos numéricos¶
O SymPy tem os tipos numéricos Rational e RealNumber. A classe Rational representa um número racional como um par de dois inteiros: o numerador e o denominador, então Rational(1,2) representa 1/2, Rational(5,2) representa 5/2, e assim por diante.
from sympy import Rational
a = Rational(1, 10)
a
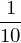
b = Rational(45, 67)
b
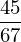
a * b
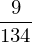
a - b
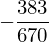
a + b
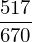
Note que a classe Rational funciona com expressões racionais exatas. Isto contrasta com o tipo de dado float, padrão do Python, que usa a representação em ponto flutuante para
aproximar números racionais.
Podemos converter o tipo sympy.Rational em uma variável de ponto flutuante no Python usando float ou o método evalf do objeto Rational. O método evalf pode levar um argumento que especifica quantos dígitos devem ser calculados para a aproximação de ponto flutuante (nem todos podem ser usados pelo tipo de ponto flutuante do Python, evidentemente).
c = Rational(2, 3)
c

float(c)
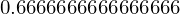
c.evalf()
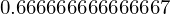
c.evalf(50)
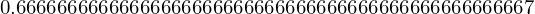
12.1.5. Diferenciação e Integração¶
O SymPy é capaz de executar a diferenciação e integração de muitas funções:
from sympy import Symbol, exp, sin, sqrt, diff
x = Symbol('x')
y = Symbol('y')
diff(sin(x), x)
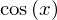
diff(sin(x), y)
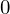
diff(10 + 3*x + 4*y + 10*x**2 + x**9, x)
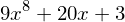
diff(10 + 3*x + 4*y + 10*x**2 + x**9, y)
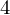
diff(10 + 3*x + 4*y + 10*x**2 + x**9, x).subs(x,1)
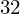
diff(10 + 3*x + 4*y + 10*x**2 + x**9, x).subs(x,1.5)
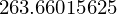
diff(exp(x), x)
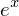
diff(exp(-x ** 2 / 2), x)
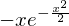
A função SymPy diff() usa no mínimo dois argumentos: a função a ser diferenciada e a variável em relação à qual a diferenciação é realizada. Derivadas de ordem superior podem ser calculadas pela especificação de variáveis adicionais, ou pela adição de um argumento inteiro opcional:
diff(3*x**4, x)
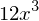
diff(3*x**4, x, x, x)
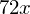
diff(3*x**4, x, 3)
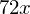
diff(3*x**4*y**7, x, 2, y, 2)
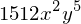
diff(diff(3*x**4*y**7, x, x), y, y)
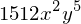
Às vezes, o SymPy pode retornar um resultado de uma forma pouco familiar. Se, por exemplo, você desejar usar o SymPy para verificar se você diferenciou algo corretamente, uma técnica que pode ser útil é subtrair o resultado do SymPy do seu resultado e verificar se a resposta é zero.
Tomando o exemplo simples de uma função de base radial multiquádrica, \(\phi(r) = \sqrt{r^2 + \sigma^2}\) com \(r = \sqrt{x^2 + y^2}\) e \(\sigma\) uma constante, podemos verificar se a primeira derivada em \(x\) é \(\frac{\partial \phi}{\partial x} = \frac{x}{\sqrt{r^2 + \sigma^ 2}}\).
Neste exemplo, primeiro pedimos que o SymPy imprima a derivada. Veja que ela é impressa de forma diferente da nossa derivada de teste, mas a subtração verifica que elas são idênticas:
r = sqrt(x**2 + y**2)
sigma = Symbol('σ')
def phi(x,y,sigma):
return sqrt(x**2 + y**2 + sigma**2)
minha_dfdx= x/sqrt(r**2 + sigma**2)
print(diff(phi(x, y, sigma), x))
x/sqrt(x**2 + y**2 + σ**2)
print(minha_dfdx - diff(phi(x, y, sigma), x))
0
Aqui é trivial dizer que as expressões são idênticas sem a ajuda do SymPy, mas, em exemplos mais complicados, pode haver muitos outros termos, tornando-se cada vez mais difícil, demorado e propenso a erros tentar reorganizar nossa derivada de teste e a resposta do SymPy na mesma forma. São nesses casos que esta técnica de subtração é de maior utilidade. A integração usa uma sintaxe semelhante. Para o caso indefinido, especifique a função e a variável em relação à qual a integração é realizada:
from sympy import integrate
integrate(x**2, x)
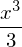
integrate(x**2, y)
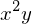
integrate(sin(x), y)
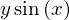
integrate(sin(x), x)
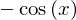
integrate(-x*exp(-x**2/2), x)
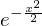
Podemos calcular integrais definidas fornecendo integrate() com uma tupla contendo a variável de interesse, os limites inferior e superior. Se várias variáveis forem especificadas, a integração múltipla é realizada. Quando o SymPy retorna um resultado na classe Rational, é possível avaliá-lo em uma representação de ponto flutuante com qualquer precisão desejada.
integrate(x*2, (x, 0, 1))
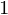
integrate(x**2, x)
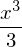
integrate(x**2, x, x)
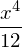
integrate(x**2, x, x, y)
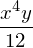
integrate(x**2, (x, 0, 2))

integrate(x**2, (x, 0, 2), (x, 0, 2), (y, 0, 1))
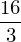
float(integrate(x**2, (x, 0, 2)))
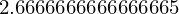
type(integrate(x**2, (x, 0, 2)))
sympy.core.numbers.Rational
resultado_racional=integrate(x**2, (x, 0, 2))
resultado_racional.evalf()
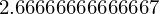
resultado_racional.evalf(50)
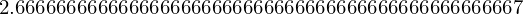
12.1.6. Equações diferenciais ordinárias¶
O SymPy tem suporte incorporado para resolver vários tipos de equações diferenciais ordinárias através do comando dsolve. Precisamos configurar a EDO e passá-la como o primeiro argumento, eq. O segundo argumento é a função f(x) a resolver. Um terceiro argumento opcional, hint, influencia o método que dsolve usa: alguns métodos são mais adequados a certas classes de EDOs ou expressarão a solução de forma mais simples do que outros.
Para configurar o solucionador de EDO, precisamos de alguma maneira, fazer referencia à função incógnita que estamos resolvendo, bem como às suas derivadas. As classes Function e Derivative facilitam isso:
from sympy import Symbol, dsolve, Function, Derivative, Eq
y = Function("y")
x = Symbol('x')
y_ = Derivative(y(x), x)
dsolve(y_ + 5*y(x), y(x))
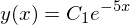
Observe como dsolve introduziu uma constante de integração, C1. Esta função introduzirá tantas constantes quantas forem necessárias, e todas serão chamadas Cn, onde n é um número inteiro. Observe também que o primeiro argumento para dsolve é considerado igual a zero, a menos que usemos a função Eq() para especificar o contrário:
dsolve(y_ + 5*y(x), y(x))
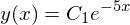
dsolve(Eq(y_ + 5*y(x), 0), y(x))
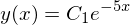
dsolve(Eq(y_ + 5*y(x), 12), y(x))
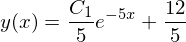
Os resultados de dsolve são uma instância da classe Equality. Isto tem consequências quando desejamos avaliar numericamente a função e usar o resultado em outro lugar (e.g. se quisermos plotar y(x) por x), porque mesmo depois de usar subs() e evalf(), ainda temos uma Equality, e não um escalar. A maneira de avaliar a função para um número é através do atributo rhs da Equality. Note que, aqui, usamos z para armazenar a Equality retornada por dsolve, ainda que seja uma expressão para uma função chamada y(x), enfatizando a distinção entre Equality e os dados que ela contém.
z = dsolve(y_ + 5*y(x), y(x))
z
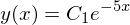
type(z)
sympy.core.relational.Equality
z.rhs
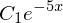
C1=Symbol('C1')
y3 = z.subs({C1:2, x:3})
y3
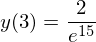
y3.evalf(10)
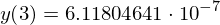
y3.rhs
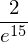
y3.evalf(10)
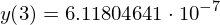
y3.rhs
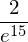
y3.rhs.evalf(10)
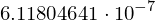
z.rhs.subs({C1:2, x:4}).evalf(10)
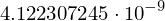
z.rhs.subs({C1:2, x:5}).evalf(10)
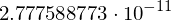
type(z.rhs.subs({C1:2, x:5}).evalf(10))
sympy.core.numbers.Float
Às vezes, dsolve pode retornar uma solução muito geral. Um exemplo é quando existe a possibilidade de que alguns coeficientes sejam complexos. Se soubermos que, por exemplo, eles são sempre reais e positivos, podemos passar esta informação para dsolve e evitar que a solução se torne desnecessariamente complicada:
from sympy import *
a, x = symbols('a,x')
f = Function('f')
dsolve(Derivative(f(x), x, 2) + a**4*f(x), f(x))
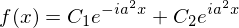
a=Symbol('a',real=True,positive=True)
dsolve(Derivative(f(x), x, 2)+a**4*f(x), f(x))
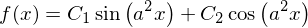
12.1.7. Expansões em série e plotagens¶
É possível expandir muitas expressões do SymPy em série de Taylor. O método series torna isso direto. No mínimo, devemos especificar a expressão e a variável a ser expandida. Opcionalmente, também podemos especificar o ponto em torno do qual expandir, o número máximo de termos e a direção da expansão (tente help(Basic.series) para mais informações).
from sympy import *
x = Symbol('x')
sin(x).series(x, 0)
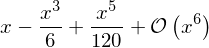
series(sin(x), x, 0)
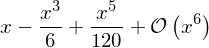
cos(x).series(x, 0.5, 10)
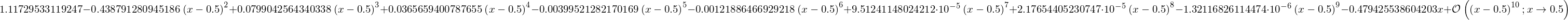
Em alguns casos, especialmente para avaliação numérica e plotagem dos resultados, é necessário remover o termo final O (n):
cos(x).series(x, 0.5, 10).removeO()
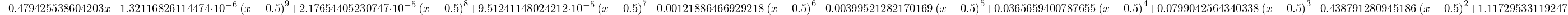
O SymPy fornece duas funções de plotagem, plot(), do módulo sympy.plotting, e plot do módulo sympy.mpmath.visualization. No momento da escrita, essas funções careciam de algumas capacidades de plotagem, o que significa que não são adequadas para a maioria de nossas necessidades. Ainda assim, caso você deseje utilizá-las, a função help() delas é útil.
Para a maioria dos nossos propósitos, Matplotlib deve ser a ferramenta de plotagem a ser escolhida. Aqui, fornecemos apenas um exemplo de como plotar os resultados de uma computação SymPy.
%matplotlib inline
from sympy import sin,series,Symbol
import pylab
x = Symbol('x')
s10 = sin(x).series(x,0,10).removeO()
s20 = sin(x).series(x,0,20).removeO()
s = sin(x)
xx = []
y10 = []
y20 = []
y = []
for i in range(1000):
xx.append(i / 100.0)
y10.append(float(s10.subs({x:i/100.0})))
y20.append(float(s20.subs({x:i/100.0})))
y.append(float(s.subs({x:i/100.0})))
pylab.figure()
<matplotlib.figure.Figure at 0x1140d6c50>
<matplotlib.figure.Figure at 0x1140d6c50>
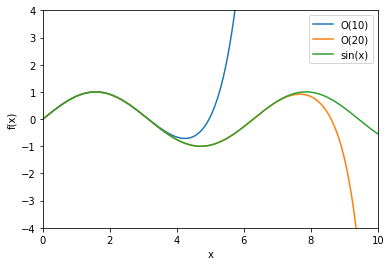
pylab.plot(xx, y10, label='O(10)')
pylab.plot(xx, y20, label='O(20)')
pylab.plot(xx, y, label='sin(x)')
pylab.axis([0, 10, -4, 4])
pylab.xlabel('x')
pylab.ylabel('f(x)')
pylab.legend()
<matplotlib.legend.Legend at 0x1143f4a58>
12.1.8. Equações lineares e inversão de matrizes¶
O SymPy possui uma classe Matrix e funções associadas que permitem a solução simbólica de sistemas de equações lineares (e, claro, podemos obter respostas numéricas com subs() e evalf()). Considerararemos o exemplo do seguinte par de equações lineares simples:
Podemos escrever este sistema na forma \(\textbf{A} \textbf{x} = \textbf{b}\) (multiplique \(\textbf{A}\) por \(\textbf{x}\) caso queira verificar se as equações originais são recuperadas), onde
Aqui, incluímos um símbolo, \(z\), no lado direito para demonstrar que os símbolos serão propagados na solução. Em muitos casos, teríamos \(z = 1\), mas ainda pode haver benefício ao se usar SymPy como um solucionador numérico, mesmo quando a solução não contenha símbolos, devido à sua capacidade de retornar frações exatas em vez de floats aproximados.
Uma estratégia para resolver o sistema para \(\textbf{x}\) é inverter a matriz \(\textbf{A}\) e pré-multiplicar a equação pela matriz inversa, i.e. \(\textbf{A}^{-1} \textbf{A} \textbf{x} = \textbf{x} = \textbf{A}^{-1} \textbf{b}\). A classe Matrix do SymPy possui um método inv() que nos permite encontrar a inversa e * realiza a multiplicação da matriz para nós, quando apropriado:
from sympy import symbols,Matrix
x, y, z = symbols('x,y,z')
A = Matrix(([3, 7], [4, -2]))
A
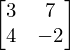
A.inv()
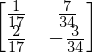
b = Matrix(( 12*z,5*z ))
b
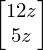
x = A.inv()*b
x

x.subs({z:3.3}).evalf(4)
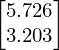
type(x)
sympy.matrices.dense.MutableDenseMatrix
Um método alternativo para resolver o mesmo problema é construir o sistema como uma matriz aumentada. Essa é a forma obtida dispondo juntas as colunas (no nosso exemplo) de \(\textbf{A}\) e o vetor \(\textbf{b}\). A matriz aumentada é [1]:
e, como antes, construímos isto como um objeto SymPy Matrix, mas, neste caso, passamos para a função solve_linear_system():
from sympy import Matrix, symbols, solve_linear_system
x, y, z = symbols('x,y,z')
system = Matrix(([3, 7, 12*z],[4, -2, 5*z]))
system
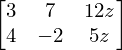
sol = solve_linear_system(system,x,y)
sol
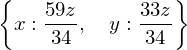
type(sol)
dict
for k in sol.keys():
print(k,'=',sol[k].subs({z:3.3}).evalf(4))
x = 5.726
y = 3.203
Uma terceira opção é o método solve(), cujos argumentos incluem as equações simbólicas individuais, em vez de matrizes. Como dsolve(), solve() espera ou expressões que ela assumirá como iguais a zero, ou objetos Equality, que podemos criar convenientemente com Eq():
from sympy import symbols,solve,Eq
x, y, z = symbols('x,y,z')
solve((Eq(3*x+7*y,12*z), Eq(4*x-2*y,5*z)), x, y)
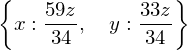
solve((3*x+7*y-12*z, 4*x-2*y-5*z), x, y)
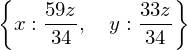
Para obter mais informações, consulte help(solve) e help(solve_linear_system).
12.1.9. Equações não-lineares¶
Vamos resolver uma equação simples como \(x = x^2\). Existem duas soluções óbvias: \(x = 0\) e \(x = 1\). Como podemos pedir ao SymPy para calcular isso para nós?
import sympy
x, y, z = sympy.symbols('x, y, z') # cria alguns símbolos
eq = x - x ** 2 # define a equação
sympy.solve(eq, x) # resolve eq = 0

A função solve() espera uma expressão que deve ser resolvida com o zero isolado. Para o nosso exemplo, reescrevemos \(x = x^2\) como \(x - x^2 = 0\) e, em seguida, a passamos para a função solve().
Vamos repetir o mesmo para a equação \(x = x^3\) e resolver
eq = x - x ** 3 # define a equação
sympy.solve(eq, x) # resolve eq = 0
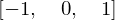
12.1.10. Saída: interface com LaTeX e impressão elegante¶
Como é o caso de muitos sistemas algébricos computacionais, o SymPy tem a capacidade de formatar sua saída como código LaTeX para facilitar sua inclusão em documentos.
No início deste capítulo, chamamos:
sympy.init_printing()
O SymPy detectou que estava em Jupyter e habilitou a saída em LaTeX. O Jupyter Notebook suporta (um pouco de) LaTeX e isso é o que nos proporciona a saída elegantemente formatada vista acima. Também podemos ver a saída em texto simples a partir do SymPy, e o código LaTeX puro que pode ser gerado:
print(series(1/(x+y), y, 0, 3))
y**2/x**3 - y/x**2 + 1/x + O(y**3)
print(latex(series(1/(x+y), y, 0, 3)))
\frac{y^{2}}{x^{3}} - \frac{y}{x^{2}} + \frac{1}{x} + \mathcal{O}\left(y^{3}\right)
print(latex(series(1/(x+y), y, 0, 3), mode='inline'))
$\frac{y^{2}}{x^{3}} - \frac{y}{x^{2}} + 1 / x + \mathcal{O}\left(y^{3}\right)$
Esteja ciente de que em seu modo padrão, o código de saída produzido por latex() requer o pacote amsmath, a ser carregado através do comando \usepackage amsmath} no preâmbulo do documento.
O SymPy também suporta uma rotina de “impressão elegante” com a função pprint() (abreviatura de “pretty print”), que produz saída de texto com melhor formatação do que a rotina de impressão padrão. Observe os recursos de notação, tais como subíndices para elementos de um array cujos nomes são da forma T_n, a constante italicizada \(e\), pontos centralizados verticalmente para a multiplicação, bordas de matrizes e frações.
Finalmente, o SymPy oferece a função preview(), que exibe a saída renderizada na tela (verifique help(preview) para obter detalhes).
12.1.11. Geração automática de código em C¶
Um ponto forte de muitas bibliotecas simbólicas é que elas podem converter as expressões simbólicas em código C (ou outro código), o qual, posteriormente, pode ser compilado para execução em alta velocidade. Aqui está um exemplo que demonstra isso:
from sympy import *
from sympy.utilities.codegen import codegen
x = Symbol('x')
sin(x).series(x, 0, 6)
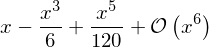
print(codegen(("taylor_sine",sin(x).series(x,0,6)), language='C')[0][1])
/******************************************************************************
* Code generated with sympy 1.0 *
* *
* See http://www.sympy.org/ for more information. *
* *
* This file is part of 'project' *
******************************************************************************/
#include "taylor_sine.h"
#include <math.h>
double taylor_sine(double x) {
double taylor_sine_result;
taylor_sine_result = x - 1.0L/6.0L*pow(x, 3) + (1.0L/120.0L)*pow(x, 5) + O(x**6);
return taylor_sine_result;
}
12.2. Ferramentas relacionadas¶
Vale a pena conferir a iniciativa SAGE (http://www.sagemath.org/), que está tentando “criar uma alternativa de fonte aberta livre e viável para Magma, Maple, Mathematica e Matlab” e inclui a biblioteca SymPy e muitas outras. Suas capacidades simbólicas são mais poderosas do que as do SymPy e o SAGE, à exceção dos recursos do SymPy, já cobrirá muitas das necessidades emergentes nos campos das ciências e engenharias. O SAGE inclui o sistema algébrico computacional Maxima, que também está disponível de forma autônoma em http://maxima.sourceforge.net/.
