14. Implementação do método da secante

Neste capítulo, utilizamos uma implementação própria do método da secante para resolver equações não-lineares unidimensionais. O algoritmo é capaz de lidar com uma quantidade razoável de funções matemáticas.

Para ser executado, o método secante requer 5 parâmetros:

• estimativas iniciais xa e xb;

• a função \(f(x)\) propriamente dita, representada por f;

• o erro relativo desejado \(ER\), representado por tol;

• o número máximo de iterações \(N\) para tentativa de solução, representado por N.

import inspect, re
import numpy as np
import matplotlib.pyplot as plt
from prettytable import PrettyTable as pt

def secante(xa,xb,f,tol,N):
    """Algoritmo para determinação de raízes pelo método da secante.

    Parâmetros: 
        f: string dependendo de uma variável, i.e., a função-alvo
            (e.g., 'x**2 - 1', 'x**2*cos(x)', etc.) 
        xa: 1a. estimativa 
        xb: 2a. estimativa        
        tol: erro relativo desejado (tolerância)
        N: número máximo de iterações a repetir

    Retorno: 
        x: aproximação para a raiz da função
    """

    # construtor de tabela
    table = pt()
    
    # substitui expressões da string pelas chamadas das funções do numpy
    f = re.sub('(sin|sinh|cos|cosh|tan|tanh|exp|log|sqrt|log10|arcsin|arccos|arctan|arcsinh|arccosh|arctanh)', r'np.\1', f)    
    
    # identifica a variável independente em f
    var = re.search(r'([a-zA-Z][\w]*) ?([\+\-\/*]|$|\))', f).group(1)
    
    # cria função
    f = eval('lambda ' + var + ' :' + f)
    
    # checa se a função é de uma variável, senão lança erro        
    try: 
        len(inspect.getfullargspec(f).args) - 1 > 0
    except:
        raise ValueError('O código é válido apenas para uma variável.')
    
    it = 0 # contador de iteracoes
    
    # cabeçalho de tabela
    table.field_names = ['i','x','f(x)','ER']

    # imprime estimativa inicial
    print(f'Estimativas iniciais: xa = {xa:.6f}; xb = {xb:.6f}\n')  

    # Loop 
    for i in range(0,N):
        
        x = (xa*f(xb) - xb*f(xa))/(f(xb) - f(xa))
        
        e = abs(x-xb)/abs(x) # erro
        
        # tabela
        # impressão de tabela
        table.add_row([i,np.round(x,8),np.round(f(x),8),f'{e:e}'])
        table.align = 'c';      
        
        if e < tol:
            break
        xa = xb
        xb = x                
        
    print(table)
       
    if i == N:
        print(f'Solução não obtida em {N:d} iterações')
    else:
        print(f'Solução obtida: x = {x:.6f}')

    return x

14.1. Problema

Determinar a raiz positiva da equação: \(f(x) = \sqrt{x} - 2e^{-2x}\), pelo método das secantes com erro inferior a \(10^{-5}\).

14.1.1. Resolução

Para obter os valores iniciais \(x_0\) e \(x_1\) necessários ao processo iterativo do método das secantes, fazemos a análise gráfica.

def f(x):
    return np.sqrt(x) - 2*np.exp(-2*x) 
  
x = np.linspace(0,3,100)
plt.figure(figsize=(6,3))
plt.plot(x,f(x),label='$f(x) = \\sqrt{x} - 2e^{-2x}$');
plt.axhline(y=0,color='r',linestyle=':')
plt.legend();

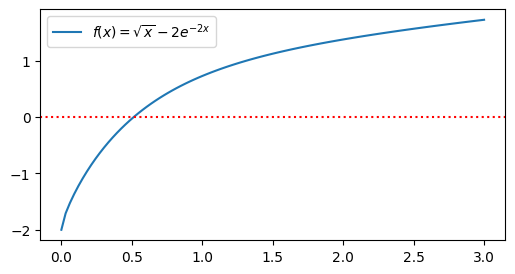
Verificamos que a raiz encontra-se próxima a \(0.5\)

f(0.5)

-0.028652101156337095

Assim, podemos escolher duas estimativas iniciais próximas deste valor, digamos \(x_0 = 0.5 - \delta x\) e \(x_1 = 0.5 + \delta x\), com \(\delta x = 10^{-1}\).

x0, dx = 0.5, 1e-1
x = secante(x0 - dx,x0 + dx,'sqrt(x) - 2*exp(-2*x)',1e-5,100)

Estimativas iniciais: xa = 0.400000; xb = 0.600000

+---+------------+-------------+--------------+
| i |     x      |     f(x)    |      ER      |
+---+------------+-------------+--------------+
| 0 | 0.52143975 |  0.01723111 | 1.506603e-01 |
| 1 | 0.51270504 | -0.00126447 | 1.703652e-02 |
| 2 | 0.5133022  |   8.57e-06  | 1.163365e-03 |
| 3 | 0.51329818 |     0.0     | 7.829741e-06 |
+---+------------+-------------+--------------+
Solução obtida: x = 0.513298

14.2. Exemplo

Resolva o problema \(f(x) = 0\), para \(f(x) = -\text{arccos}(x) + 4\text{sen}(x) + 1.7\), no intervalo \(-0.2 \le x \le 1.0\) e \(\epsilon = 10^{-3}\).

x0, dx = -0.8, 1e-1
x = secante(x0 - dx,x0 + dx,'-arccos(x) + 4*sin(x) + 1.7',1e-3,20)

Estimativas iniciais: xa = -0.900000; xb = -0.700000

+---+-------------+-------------+--------------+
| i |      x      |     f(x)    |      ER      |
+---+-------------+-------------+--------------+
| 0 |  0.01559341 |  0.20716881 | 4.589077e+01 |
| 1 | -0.02762483 | -0.00890993 | 1.564471e+00 |
| 2 | -0.02584274 |   -1.4e-06  | 6.895899e-02 |
| 3 | -0.02584246 |     0.0     | 1.082134e-05 |
+---+-------------+-------------+--------------+
Solução obtida: x = -0.025842

Resolvemos usando outras estimativas iniciais.

x0, dx = -0.9, 1e-3
x = secantes(x0 - dx,x0 + dx,'-arccos(x) + 4*sin(x) + 1.7',1e-3,20)

Estimativas iniciais: xa = -0.901000; xb = -0.899000

+---+-------------+-------------+--------------+
| i |      x      |     f(x)    |      ER      |
+---+-------------+-------------+--------------+
| 0 | -0.03737686 | -0.05765454 | 2.305231e+01 |
| 1 | -0.02514562 |  0.00348352 | 4.864164e-01 |
| 2 | -0.02584253 |   -3.5e-07  | 2.696761e-02 |
| 3 | -0.02584246 |     -0.0    | 2.747395e-06 |
+---+-------------+-------------+--------------+
Solução obtida: x = -0.025842