7. Do Vetor ao Array: Computação Vetorizada Na Prática#

Objetivos de aprendizagem

Associar conceitos abstratos de Álgebra Linear a estruturas computacionais;
Realizar operações básicas com matrizes e vetores;
Saber como resolver sistemas lineares de pequeno porte;
Reconhecer e calcular operações comuns entre matrizes e vetores;

"Como em tudo o mais, também numa teoria matemática: a beleza pode ser percebida, mas não explicada. (Arthur Cayley)"

7.1. Introdução#

Matrizes e vetores são estruturas fundamentais nas ciências aplicadas, em especial na engenharia e na computação, pois oferecem uma linguagem unificada para modelar sistemas, representar dados e realizar cálculos eficientes. Do ponto de vista algébrico, vetores podem representar estados de um sistema, enquanto matrizes atuam como operadores que transformam esses estados — como em sistemas de equações lineares usados para modelar circuitos elétricos, fluxos de calor ou estruturas mecânicas. Na economia, vetores podem representar cestas de bens ou variáveis macroeconômicas, e matrizes podem modelar interações entre setores produtivos em modelos insumo-produto. Já em engenharia computacional, matrizes são onipresentes em métodos numéricos para resolução de equações diferenciais que modela um problema físico e são discretizadas em sistemas lineares matriciais.

No plano geométrico, vetores representam pontos ou direções em espaços de qualquer dimensão, enquanto matrizes podem ser interpretadas como transformações lineares — rotações, escalamentos ou projeções — aplicadas a esses vetores. Essa visão é central, por exemplo, na computação gráfica, onde transformações matriciais controlam a renderização de cenas tridimensionais. Já na ciência de dados e no processamento de sinais, vetores de alta dimensão representam amostras de áudio, imagens ou vídeos — com cada dimensão correspondendo a um pixel, uma intensidade sonora, ou uma característica extraída. A manipulação de dados n-dimensionais, por meio de operações matriciais como multiplicação, decomposição ou diagonalização, é essencial para reduzir dimensionalidade (como na análise de componentes principais), filtrar ruído, identificar padrões e treinar modelos de aprendizado de máquina. Assim, além de seu papel teórico, matrizes e vetores são ferramentas práticas para interpretar, simular e interagir com os fenômenos complexos do mundo real.

Neste capítulo, mostraremos como realizar operações básicas entre matrizes e vetores usando o computador como utilidade para a compreensão de armazenamento de dados principalmente em estruturas uni ou bidimensionais. O estudo da relação entre algoritmos e métodos computacionais para trabalhar eficientemente com matrizes e vetores é realizado no âmbito da Álgebra Linear Computacional, porém, aqui, enfantizaremos aplicações práticas e o uso de operações comuns.

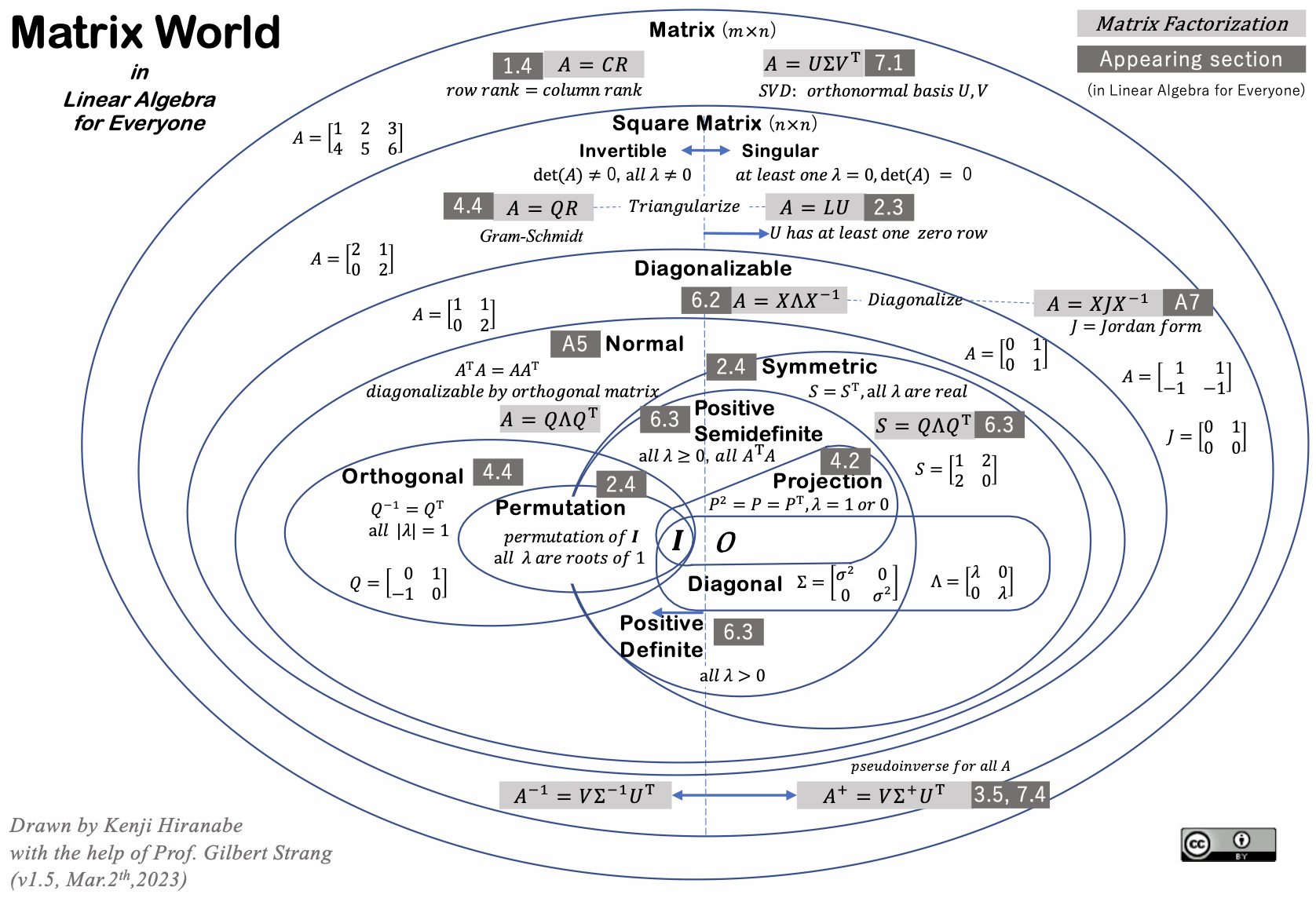
../_images/matrix-world.png — Fig. 7.1 “O mundo das matrizes”: ilustração produzida por Kenji Hiranabe e Gilbert Strang para o livro *Linear Algebra for Everyone*.#

Curiosidade: a origem da “matrix”

O termo “matriz” (matrix) deriva da palavra arcaica francesa “matrice”, que significa “útero”. Etimologicamente, está ligada à ideia de “origem”, por “mater”, de onde vem o significado de “mother” (mãe). Isso ajuda a explicar bastante o enredo da franquia de filmes “Matrix”, protagonizada por Keanu Reeves, onde o personagem Neo e seus amigos nascem em um ambiente artificial em que os corpos são cultivados em cápsulas e as mentes conectadas à Matriz, uma simulação de realidade. Surpreendentemente, essa mesma ideia é a que subsiste na matemática.

Credita-se ao matemático inglês James Joseph Sylvester (1814 - 1897) o primeiro uso do termo “matriz”, que apareceu em um artigo de sua autoria publicado em 1850. Sylvester assim disse, em tradução livre do original:

“Para esse propósito, devemos começar, não com um quadrado, mas com uma disposição retangular de termos composta, suponhamos, por m linhas e n colunas. Isso, por si só não representa um determinante, mas é, por assim dizer, uma matriz a partir da qual podemos formar diversos sistemas de determinantes ao fixarmos um número p e selecionarmos, à vontade, p linhas e p colunas — os quadrados correspondentes a essas seleções podem ser chamados de determinantes de ordem p.”

E daí nasceu o conceito de matriz, como uma associação ao que chamamos de “array” em computação. Entretanto, na Matemática, a definição de uma matriz não é tão simples quanto parece, sendo necessário compreendê-la como uma “função” que associa um espaço vetorial a outro. É por isso que nem sempre quando falamos do conceito de “dimensão” (size) ou “comprimento” (length), como atributos de arrays computacionais, existe um paralelo imediato com o conceito de dimensão (“dimension”) utilizado pela álgebra linear.

7.2. Computação vetorizada#

O conceito de computação vetorizada, ou computação baseada em arrays, está relacionado à execução de operações que podem ser feitas de uma só vez a um conjunto amplo de valores. A ideia principal da computação vetorizada é evitar laços e cálculos com repetições a fim de acelerar operações matemáticas e permite que essas estruturas multidimensionais sejam identificadas com a nossa compreensão de vetores, matrizes e tensores. Vetores são arrays unidimensionais. Matrizes são arrays bidimensionais. Tensores são arrays de três ou mais dimensões. Arrays possuem alguns atributos, tais como “comprimento”, “formato” e “dimensão, os quais dizem respeito, de certa forma, à quantidade de seus elementos e ao modo como ocupam a memória. Esses nomes variam de linguagem para linguagem. Em Python, existem funções e métodos específicos para verificar comprimento, formato e dimensão, tais como len, shape e ndim. Entretanto, esses conceitos possuem sentidos um pouco diferentes quando queremos descrever os conceitos matemáticos.

7.2.1. Comprimento, tamanho e dimensão#

Para exemplificar o que queremos dizer com “comprimento”, “tamanho” e “dimensão”, vejamos uma ilustração. Se x1 e x2 são dois números inteiros, a lista [x1,x2] seria um array unidimensional, mas de comprimento dois. Agora, imagine que \((x_1,x_2)\) seja a notação matemática para representar as coordenadas de um ponto do plano cartesiano. Sabemos da geometria que o plano cartesiano tem duas dimensões. Porém, poderíamos, computacionalmente, usar a mesma lista anterior para armazenar no computador essas duas coordenadas. A lista continuaria sendo unidimensional, porém de tamanho dois. Logo, embora a entidade matemática seja bidimensional, não necessariamente a sua representação computacional deve ser bidimensional.

Vejamos outra ilustração. Uma esfera é um sólido geométrico. Cada ponto da esfera está no espaço tridimensional. Isto significa que precisamos de 3 coordenadas para localizar cada um desses pontos. Do mesmo modo que o caso anterior, suponha que você tenha não apenas x1 e x2 como dois números inteiros, mas também um terceiro, x3, para montar as coordenadas do seu ponto espacial. Você poderia representá-lo, matematicamente, por uma tripla \((x_1,x_2,x_3)\) sem problema algum. Por outro lado, no computador, a lista [x1,x2,x3] seria um array adequado para armazenar os valores das suas coordendas. Entretanto, esta lista continuaria sendo um array unidimensional, mas com tamanho 3. Portanto, arrays unidimensionais podem representar dados em dimensões maiores do que um.

7.2.2. `numpy`#

Em Python, numpy é a ferramenta ideal para lidar com tudo isso, a biblioteca padrão em Python para trabalhar com arrays multidimensionais e computação vetorizada. Ela praticamente dá “superpoderes” às listas e permite que trabalhemos com cálculos numéricos de maneira ágil, simples e eficiente. Com numpy, também podemos ler e escrever arquivos, trabalhar com sistemas lineares e realizar muito mais. O exemplo abaixo compara a eficiência de operações feitas com listas comuns e com arrays do numpy.

import timeit
import numpy as np

# Função de teste
def test_cube(n: int, method: str):
    if method == 'numpy':        
        return np.power(np.arange(n), 3)
    elif method == 'list':
        return [i**3 for i in range(n)]
    else:
        raise ValueError("Método indefinido")

# Número de repetições para a medição do tempo
reps = 50

# Número de elementos
nel = [10, 100, 500, 1000, 5000, 10000, 50000]

# Loop para diferentes tamanhos de entrada
for n in nel:

    # Medindo o tempo de execução para o método 'list'
    t_list = timeit.timeit(lambda: test_cube(n, 'list'), number=reps)

    # Medindo o tempo de execução para o método 'numpy'
    t_numpy = timeit.timeit(lambda: test_cube(n, 'numpy'), number=reps)

    # Calculando o overhead normalizado
    overhead = (t_list - t_numpy) / t_numpy    

    # Exibindo os resultados
    #print(f"Tempo gasto com 'list' para {n} elementos: {t_list:.6f} s")
    #print(f"Tempo gasto com 'numpy' para {n} elementos: {t_numpy:.6f} s")
    print(f"Overhead normalizado para {n} elementos: {overhead:.3f}")

Overhead normalizado para 10 elementos: -0.950
Overhead normalizado para 100 elementos: 0.071
Overhead normalizado para 500 elementos: 1.645
Overhead normalizado para 1000 elementos: 9.431
Overhead normalizado para 5000 elementos: 47.239
Overhead normalizado para 10000 elementos: 51.317
Overhead normalizado para 50000 elementos: 85.217

7.3. Compreendendo notações#

A diversidade de notações utilizadas para representar vetores e matrizes reflete não apenas preferências estilísticas, mas sobretudo a influência das diferentes tradições científicas e áreas de aplicação. Vetores podem ser indicados por letras em negrito, letras com setas, letas entre colchetes e ainda por índices subscritos conforme o contexto. Na física, a notação com setas é comum; na matemática aplicada, encontra-se o uso de negrito tipográfico; nas engenharias, por vezes encontramos o uso de chaves ou colchetes para representar matrizes e também subíndices; na computação, o uso é variado.

A notação indicial, por exemplo, também conhecida como notação de Einstein — onde se assume uma soma implícita sobre índices repetidos —, é fundamental em teorias de tensores e na mecânica do contínuo, permitindo expressar operações complexas de forma compacta e elegante. A escola de Gibbs, por sua vez, introduziu notações específicas para produtos vetoriais e escalares, ainda largamente utilizadas, predominante nos símbolos em negrito. Em computação, há uma tendência a representar vetores como arrays unidimensionais e matrizes em forma tabular, alinhando a abstração matemática à estrutura de dados. Enquanto essa pluralidade de notações deve-se a fatores históricos e culturais, ela pode influenciar ativamente a maneira como os conceitos são compreendidos, manipulados e ensinados.

Para os nossos interesses, o fundamental a saber não é a notação em si, mas como os conceitos fundamentais da álgebra linear, que têm impacto em quase tudo o que fazemos com dados, são transportados para o computador a ponto de serem manipulados com precisão. O quadro abaixo resume algumas notações para operações clássicas e as áreas onde predominam.

Notação	Significado	Área(s) predominante(s)
\(\mathbf{A}, \mathbf{v}\)	matriz e vetor em negrito	Matemática, Computação
\(\vec{v}\)	vetor com seta	Física, Engenharias, Computação
\(\overrightarrow{A}\)	matriz com seta maior	Física
\(v_i\), \(A_{ij}\)	notação indicial para componente de vetor ou matriz	Matemática, Engenharias
\([a_{ij}]\), \(\{a_{ij}\}\)	matriz com notação indicial de componentes	Engenharias

Por conveniência, priorizaremos a notação em negrito.

Além do significado algébrico, geométrico ou computacional que representam nas ciências, matrizes e vetores podem ser vistos sob diferentes perspectivas que enriquecem não só a intuição, mas também a capacidade de aplicar conceitos a contextos diversos, principalmente ao se lidar com áreas computacionais. Formas interessantes de compreender matrizes e vetores através de visualizações são propostas por Kenji Hiranabe, co-autor do artigo The Art of Linear Algebra.

Dica: a origem da “matrix”

Existem vídeos excelentes com aulas do Prof. Gilbert Strang sobre como melhor enxergar a Álgebra Linear nesta página do MIT/OCW. Vale a pena assistir.

7.4. Matrizes e vetores#

Uma matriz \({\bf A}\) de ordem \(m \times n\) pode ser escrita como:

\[\begin{split}{\bf A} = \begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{bmatrix}\end{split}\]

As colunas de uma matriz com \(m\) linhas correspondem a \(n\) vetores \(\vec{v}_1, \vec{v}_2, \ldots,\vec{v}_n\), de maneira que

\[\begin{split}{\bf A} = \begin{bmatrix} \vec{v}_1 & \vec{v}_2 & \ldots & \vec{v}_n \\ \end{bmatrix}\end{split}\]

é uma representação equivalente para a matriz anterior.

Em Python, usamos o módulo numpy para trabalhar com matrizes e vetores. Vetores são arrays 1D, ao passo que matrizes são arrays 2D, ou seja, um “array de arrays”.

Exemplo. Represente computacionalmente os vetores do \(\mathbb{R}^3\) a seguir:

\(\vec{u} = 3\vec{i} - 2\vec{j} + 9\vec{k}\)
\(\vec{v} = -2\vec{i} + 4\vec{j}\)
\(\vec{w} = \vec{i}\)

Curiosidade: ndarray

O NumPy possui uma classe especial para se trabalhar com matrizes e vetores em uma ou duas dimensões, a saber o tipo matrix, ou mat. Com objetos matrix, as operações particulares de multiplicação matriz-matriz ou matriz-vetor comportam-se diferentemente daquelas na classe ndarray. Neste texto, abordaremos apenas os tipos ndarray porque são aplicáveis também a matrizes multidimensionais.

import numpy as np

u = np.array([3,-2,9])
v = np.array([-2,4,0])
w = np.array([1,0,0])
print(u), print(v), print(w);

[ 3 -2  9]
[-2  4  0]
[1 0 0]

Exemplo. Represente computacionalmente a matriz 3 x 3 dada por

\[\begin{split}{\bf A} = \begin{bmatrix} \vec{u} & \vec{v} & \vec{w} \\ \end{bmatrix}\end{split}\]

Observe que os vetores devem ser escritos como “coluna”.

A = np.array([u,v,w]).T

Exemplo. Represente computacionalmente a matriz

\[\begin{split} \begin{bmatrix} 2 & -2 \\ 4 & 1 \\ 2 & 1 \end{bmatrix}\end{split}\]

Vamos escrever linha por linha.

L1 = np.array([2,-2]) # linha 1
L2 = np.array([4,1]) # linha 2
L3 = np.array([2,1]) # linha 3

A2 = np.array([L1,L2,L3]) # lista de listas
print(A2)

[[ 2 -2]
 [ 4  1]
 [ 2  1]]

Diretamente, poderíamos também definir:

A3 = np.array([[2,-2],[4,1],[2,1]])
print(A3)

[[ 2 -2]
 [ 4  1]
 [ 2  1]]

Note que cada lista representa uma linha.

7.4.1. Transposição#

Matrizes e vetores podem ser transpostos com .T:

A2T = A2.T
print(A2T)

[[ 2  4  2]
 [-2  1  1]]

uu0 = [1,2,3]
uu1 = np.array(uu0)
type(uu0), type(uu1)

(list, numpy.ndarray)

Assim, com as variáveis antes definidas, poderíamos, equivalentemente, fazer para \({\bf A}\):

# modo 2: matriz transposta
At = np.array([u,v,w]).T 
print(At)

[[ 3 -2  1]
 [-2  4  0]
 [ 9  0  0]]

7.4.2. Teste de igualdade#

Podemos verificar a igualdade entre matrizes como

np.array([np.array([1,2,3]), np.array([-4,2,1]), np.array([3,3,1])])

array([[ 1,  2,  3],
       [-4,  2,  1],
       [ 3,  3,  1]])

No caso de vetores:

# vetor "linha" não difere
# do vetor "coluna"
u == u.T 

array([ True,  True,  True])

7.5. Operações fundamentais#

Veremos algumas operações fundamentais entre matrizes e vetores e destacar algumas, como as do quadro abaixo.

Nome em Português	Nome em Inglês	Notações Comuns	Exemplo de Aplicação
Produto escalar ou interno	scalar (or dot) product	\( \mathbf{u} \cdot \mathbf{v} \), \( \mathbf{u}^T \mathbf{v} \)	Similaridade entre dois vetores
Produto tensorial (diádico)	tensor (outer) product	\( \mathbf{u} \otimes \mathbf{v} \), \(\mathbf{u} \mathbf{v}\)	Gerar uma matriz a partir de dois vetores
Produto vetorial	cross product	\( \mathbf{u} \times \mathbf{v} \)	Calcular a direção perpendicular a dois vetores em 3D
Produto elemento-a-elemento	Hadamard (or Schur) product	\( \mathbf{u} \circ \mathbf{v} \), \( \mathbf{u} \odot \mathbf{v} \)	Operações de redes neurais e métodos numéricos
Produto escalar	Fröbenius inner product	\( \langle A, B \rangle \)	Produto escalar entre duas matrizes

Notas:

o símbolo \(\otimes\) também é usado para denotar o produto de Kronecker.
na operação \(\mathbf{u} \mathbf{v}\), quando originalmente chamada de “produto externo”, \(\mathbf{u}\) é um vetor coluna e \(\mathbf{v}\) é um vetor linha. No Brasil, o o termo “produto externo” é menos frequente e usado como sinônimo de produto vetorial.
na operação \(\mathbf{u}^T \mathbf{v}\), exibida como outra forma de produto interno, \(\mathbf{u}\) e \(\mathbf{v}\) são vetores coluna.

Curiosidade: produto exterior

Na Geometria Diferencial, estuda-se o “Cálculo Diferencial Exterior”, e lá se define também outer product como “produto exterior”, o que também é conhecido internacionalmente como wedge product, denotado por \(\mathbf{u} \wedge \mathbf{v}\), que é uma operação que combina dois vetores para produzir um elemento de ordem superior. Como nesta geometria estudam-se curvas e superfícies, o produto externo é frequentemente usado para definir grandezas como área e volume.

7.5.1. Adição e subtração#

A adição (subtração) de matrizes e vetores pode ser realizada de modo usual com computação vetorizada.

Exemplo: \(\vec{u} \pm \vec{v}\)

# adição 
ad = u + v
print(ad)

# subtração
sub = u - v
print(sub)

[1 2 9]
[ 5 -6  9]

Exemplo: \(\bf{A} \pm \bf{B}\), com

\[\begin{split}{\bf B} = \begin{bmatrix} \vec{u} & 2\vec{u} & 3\vec{v} \\ \end{bmatrix}\end{split}\]

# adição

B = np.array([u,2*u,3*v]).T

ad2 = A + B
print(ad2)

sub2 = A - B
print(sub2)

[[ 6  4 -5]
 [-4  0 12]
 [18 18  0]]
[[  0  -8   7]
 [  0   8 -12]
 [  0 -18   0]]

7.5.2. Produto interno#

O produto interno \(\langle \vec{u}, \vec{v}\rangle\) é computado com .dot:

pi = np.dot(u,v)
print(pi)

pi2 = np.dot(np.array([3,1]),np.array([-1,-1]))
print(pi2)

-14
-4

Uma segunda forma, mais imediata, emprega o operador infixo @:

pii = u @ v
print(pii)

pii2 = np.array([3,1]) @ np.array([-1,-1])
print(pii2)

-14
-4

7.5.3. Norma de vetor#

A norma \(||\vec{u}||\) de um vetor \(\vec{u}\) é calculada como:

np.sqrt(np.dot(u,u))

np.float64(9.695359714832659)

7.5.4. Produto de matrizes#

O produto \(\bf{A}\bf{B}\) entre matrizes bidimensionais pode ser calculado com np.dot, mas recomenda-se usar np.matmul.

# não tem o mesmo efeito para 
# matrizes A e B de tamanhos arbitrários
np.dot(A,B)

array([[ 22,  44, -42],
       [-14, -28,  60],
       [ 27,  54, -54]])

# uso recomendado para a operação tradicional
np.matmul(A,B)

array([[ 22,  44, -42],
       [-14, -28,  60],
       [ 27,  54, -54]])

7.5.5. Produto entre matriz e vetor#

Neste caso, sendo \({\vec{\vec A}}\) (dois símbolos indicam que a matriz é uma grandeza de ordem 2, ao passo que o vetor é de ordem 1 e aqui usamos para consistência de notação) uma matriz \(m \times n\) e \({\vec{b}}\) e um vetor \(n \times 1\), respectivamente, o produto \(\vec{\vec{A}}\vec{b}\) é dado por:

b = np.array([3,4,1])

np.dot(A,b)

array([ 2, 10, 27])

7.6. Demais operações com `numpy.linalg`#

Para outras operações, devemos utilizar o submódulo numpy.linalg. Para importá-lo com o alias lin, fazemos:

import numpy.linalg as lin

7.6.1. Determinante#

O determinante de \({\bf A}\) é dado por \(\det({\bf A})\) e pode ser computado pela função det.

# calculando o determinante da matriz
det = lin.det(A)
print(det)

-36.0

7.6.2. Inversa de uma matriz#

A inversa de uma matriz é dada por \({\bf A}^{-1}\), onde \({\bf A}{\bf A}^{-1}={\bf I}\), e \({\bf I}\) é a matriz identidade. Para usar esta função, devemos fazer:

B2 = np.array([[1,2,3],
              [2,3,4],
              [1,2,0]]) 

B3 = lin.inv(B2)
np.matmul(B3,B2) == np.eye(3)

array([[ True, False,  True],
       [False, False,  True],
       [ True,  True,  True]])

7.6.3. Inversa de matriz#

A inversa de uma matriz (faça esta operação apenas para matrizes quadradas de pequena dimensão) pode ser encontrada como:

Ainv = lin.inv(A)
print(Ainv)

[[-0.40333333  0.2         0.21333333]
 [ 0.46333333 -0.2        -0.25333333]
 [-0.00333333  0.          0.01333333]]

Para realizar uma “prova real” da solução do sistema anterior, poderíamos fazer:

x2 = np.dot(lin.inv(A), b)
print(x2)

[-3.90666667  5.82666667  0.69333333]

Note, entretanto que:

x == x2

array([False, False,  True])

Isto ocorre devido a erros numéricos. Um teste mais adequado deve computar a norma do vetor “erro”, dado por \({\bf e} = \bf{b} - \bf{A}\bf{x}\). A norma pode ser calculada diretamente com:

e = b - np.dot(A,x)
lin.norm(e)

np.float64(0.0)

Isto é, esperamos que \(||{\bf e}|| \approx 0\) quando a solução do sistema for exata, a menos de erros numéricos.

Warning

Nunca compare dois números reais (float) usando igualdade. Ou seja, x == y, não é, em geral, um bom teste lógico para verificar se x e y possuem o mesmo valor numérico.

7.7. Algumas matrizes especiais#

7.7.1. Nula#

Para criar uma matriz nula de ordem m x n, usamos zeros.

m,n = 2,6
np.zeros((m,n))

array([[0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0.]])

7.7.2. Identidade#

Uma matriz identidade (quadrada) de ordem p é criada com eye.

p = 4
np.eye(p)

array([[1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.]])

7.7.3. Matriz de “uns”#

Uma matriz composta apenas de valores 1 de ordem m x n pode ser criada com ones:

np.ones((3,5))

array([[1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.]])

7.7.4. Triangular inferior#

A matriz triangular inferior de uma dada matriz pode ser criada com tril. Note que podemos também defini-la explicitamente, linha a linha.

# os valores correspondentes
# são zerados
np.tril(B)

array([[ 3,  0,  0],
       [-2, -4,  0],
       [ 9, 18,  0]])

7.7.5. Triangular superior#

A matriz triangular superior de uma dada matriz pode ser criada com triu. Note que podemos também defini-la explicitamente, linha a linha.

np.triu(B)

array([[ 3,  6, -6],
       [ 0, -4, 12],
       [ 0,  0,  0]])

Exercício. Por que há dois valores False no teste a seguir?

B == np.tril(B) + np.triu(B)

array([[False,  True,  True],
       [ True, False,  True],
       [ True,  True,  True]])

7.8. Autovalores e autovetores#

Um vetor \({\bf v} \in V\), \({\bf v} \neq {\bf 0}\) é vetor próprio de \({\bf A}\) se existir \(\lambda \in \mathbb{R}\) tal que

\[{\bf Av}=\lambda {\bf v}.\]

O número real \(\lambda\) é denominado valor próprio (autovalor) de \({\bf A}\) associado ao vetor próprio (autovetor) \({\bf v}\).

A = np.array([[2,1],
              [1,-5]])

w, v = lin.eig(A)
a,b = w

# autovalores
print(a,b)

# autovetor 1
print(v[:,0])

# autovetor 2
print(v[:,1])

2.1400549446402586 -5.1400549446402595
[0.99033427 0.13870121]
[-0.13870121  0.99033427]

7.9. Somas e valores extremos#

Podemos calcular somas de elementos de matrizes e vetores de maneiras diferentes. Para matrizes, em particular, há soma total, por linha, ou por coluna.

a = np.array([1,-2,-3,10])

# soma de todos os elementos 
np.sum(a)

np.int64(6)

# modo alternativo
a.sum() 

np.int64(6)

# soma total de matriz
O = np.ones((5,3))

np.sum(O)

np.float64(15.0)

# modo alternativo
O.sum()

np.float64(15.0)

# soma por linha 

M = np.array( [ [ [ [-1,0],[1,0] ], [ [-1,0],[1,0] ]] ])

np.sum(M,axis=3)

array([[[-1,  1],
        [-1,  1]]])

# soma por coluna 
np.sum(O,axis=1)

array([3., 3., 3., 3., 3.])

Valores máximos e mínimos, absolutos ou não, também podem ser computados com funções simples.

# min
np.min(a)

np.int64(-3)

# max
np.max(a)

np.int64(10)

# modo alternativo
a.min()

np.int64(-3)

a.max()

np.int64(10)

# mínimo absoluto 
np.abs(a).min()

np.int64(1)

# máximo absoluto
np.abs(a).max()

np.int64(10)

O2 = np.array([[-4,5],[2,7]])

# min
np.min(O2)

np.int64(-4)

# max 
np.max(O2)

np.int64(7)

O2.min()

np.int64(-4)

O2.max()

np.int64(7)

np.abs(O2).min()

np.int64(2)

np.abs(O2).max()

np.int64(7)

np.min( np.array([[1,-2,-3], [0,0,4]]), axis=0)

array([ 0, -2, -3])

Métodos Numéricos para Ciências Computacionais e Engenharia

Do Vetor ao Array: Computação Vetorizada Na Prática

Contents

7. Do Vetor ao Array: Computação Vetorizada Na Prática#

Objetivos de aprendizagem

7.1. Introdução#

7.2. Computação vetorizada#

7.2.1. Comprimento, tamanho e dimensão#

7.2.2. `numpy`#

7.3. Compreendendo notações#

7.4. Matrizes e vetores#

7.4.1. Transposição#

7.4.2. Teste de igualdade#

7.5. Operações fundamentais#

7.5.1. Adição e subtração#

7.5.2. Produto interno#

7.5.3. Norma de vetor#

7.5.4. Produto de matrizes#

7.5.5. Produto entre matriz e vetor#

7.6. Demais operações com `numpy.linalg`#

7.6.1. Determinante#

7.6.2. Inversa de uma matriz#

7.6.3. Inversa de matriz#

7.7. Algumas matrizes especiais#

7.7.1. Nula#

7.7.2. Identidade#

7.7.3. Matriz de “uns”#

7.7.4. Triangular inferior#

7.7.5. Triangular superior#

7.8. Autovalores e autovetores#

7.9. Somas e valores extremos#

Métodos Numéricos para Ciências Computacionais e Engenharia

Do Vetor ao Array: Computação Vetorizada Na Prática

Contents

7. Do Vetor ao Array: Computação Vetorizada Na Prática#

Objetivos de aprendizagem

7.1. Introdução#

7.2. Computação vetorizada#

7.2.1. Comprimento, tamanho e dimensão#

7.2.2. numpy#

7.3. Compreendendo notações#

7.4. Matrizes e vetores#

7.4.1. Transposição#

7.4.2. Teste de igualdade#

7.5. Operações fundamentais#

7.5.1. Adição e subtração#

7.5.2. Produto interno#

7.5.3. Norma de vetor#

7.5.4. Produto de matrizes#

7.5.5. Produto entre matriz e vetor#

7.6. Demais operações com numpy.linalg#

7.6.1. Determinante#

7.6.2. Inversa de uma matriz#

7.6.3. Inversa de matriz#

7.7. Algumas matrizes especiais#

7.7.1. Nula#

7.7.2. Identidade#

7.7.3. Matriz de “uns”#

7.7.4. Triangular inferior#

7.7.5. Triangular superior#

7.8. Autovalores e autovetores#

7.9. Somas e valores extremos#

7.2.2. `numpy`#

7.6. Demais operações com `numpy.linalg`#